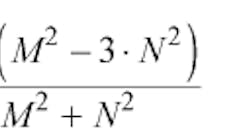Analyze Circulator Design Equations

The two equations are derived from the electromagnetic (EM) field solution for perfect circulation given by Bosma in ref. 1. Parameters P, M, and N are defined as:

where ψ is half the coupling angle at any one of the three ports and

where the J_n represent Bessel functions of the first kind with order n and

is the wave propagation constant where

ε_r = the relative dielectric constant,
f = the frequency,
c = the speed of light, and

is the effective permeability for the given Polder tensor parameters µ and κ.

Parameter Q is defined as

where the parameters Z_d and Z_eff are the external intrinsic impedance at the circulator ports and the intrinsic impedance of the magnetized ferrite, respectively. To help engineers better understand circulator design, this report will present graphic solutions for the two circulation equations at different levels of complexity.

Figures 2 and 3 represent classic solutions to the Eqs. 1 and 2 under ideal conditions and when retaining the first three terms of N and M (n = 0...2). These graphs are presented numerous times in earlier publications.^1,3 The graph in Fig. 2 gives the roots to Eq. 1 by presenting values of the electric radius, sR, as a function of |κ/µ| for various coupling angles. Figure 3 gives the roots to Eq. 2 by presenting the wave impedance ratio Z_eff/Z_d as a function of |κ/µ| for various coupling angles (half the coupling angle is denoted as ψ (Fig. 1).

There are two possible algorithms for solving Eqs. 1 and 2 for the variables sR and Z_eff/Z_d as a function of |κ/µ|. One way is to solve Eq. 1 for sR, use the obtained values of N and M to calculate Q, and then solve Eq. 2a for Z_eff/Z_d. This is an adequate way to solve the two equations but it may result in higher-order results. To avoid this, a limit is required for the acceptable range of solutions for Z_eff/Z_d. A preferred approach is to solve both equations simultaneously.

The simple solution proposed here involves solving Eq. 1 for sR under perfect conditions, i.e., no loss and for the first three terms (n = 0, 1, 2) as given in the literature for the classic solution. Each solution for sR also provides values for parameters M and N, which are then used in Eq. 2 to calculate the value of Z_eff/Z_d. A solution to Eq. 1 is within a given range, i.e., 0 < sR ≤ 3.5 with values of Z_eff/Z_d only acceptable within the range 0 ≤ (Z_eff/Z_d) ≤ 2.2.

Figures 4 and 5 show these solutions graphically, with curves identical to those in Figs. 2 and 3. The missing points are due to solutions with large error-function values (where no solutions were found, i.e., any circumstance where an error-function value exceeded 0.01). The lack of some points may also be due to differences in computational tools, i.e., personal computer (PC) versus workstation computer.

When the two equations are solved simultaneously, keeping the two variables within a given range i.e. 0 < sR ≤ 3.5 and 0 ≤ (Z_eff/Z_d) ≤ 2.2, the graphs of Figs. 6 and 7 result for the conditions used to generate Figs. 4 and 5. Other than the curves for ψ = 0.2 in Figs. 6 and 7, the other values of ψ are in close agreement with the values of Figs. 2 and 3.

Applying the DC vertical magnetic field, H_i, instigates the magnetic resonance frequency, f₀. The field intensity is chosen as the minimum required to ensure saturation (just saturated), i.e., H_i = H_m. At saturation, there is a cutoff frequency, designated f_m. The two frequencies are defined in Eqs. 3 and 4, respectively:

where:

γ_e = the gyromagnetic ratio and

4πM_s = the magnetization saturation.

Using the definition δ = f₀/f and assuming the ideal (lossless) case, the Polder parameter µ can be defined as

For each value of |κ/µ|, it is possible to directly find µ, µ_eff, and s. For the second variable, R and sR will be calculated as well. Since s is proportional to f/c and R is proportional to c/f, the product sR (the root of Eq. 1) is frequency independent. On the other hand, the solution to Eq. 2 seems to be frequency dependent at ψ = 0.2. Although there are some differences in the calculated curves for µ, µ_eff, and s (Figs. 8 to 11), the general trend is identical to Fig. 3. Figure 9 shows the results at close proximity to the cutoff frequency. Figure 10 shows the results at a higher frequency, and Fig. 11 shows the results at an even higher frequency.

The circulator's ferrite resonant material is not ideal, yielding a resonant width, ΔH, rather than a single-frequency resonance. Equation 5 relates the loss due to this resonance width:

where:

f = the frequency at which the width is measured.

At this point, it is necessary to define the parameters of the Polder Tensor. Common practice is to solve Gilbert's equation⁷:

where:

H = the DC magnetic field vector,
M = the magnetization vector,
t = the time variable,
γ_e = the gyromagnetic ratio, and
α_h = the damping magnitude coefficient.

Equation 6 is a good approximation of the Landau and Lifshitz equation⁵:

Equations 8 and 9 provide The Polder Tensor parameters:

When derived from the Gilbert's equation (Eq. 6), and using the definition p_s = f_m/f , the terms for the above equations are as follows:

For the derivation of the original Landau and Lifshitz equation (Eq. 7), the terms are different and are as follows:

Page Title

To this point, a "just saturated" state has been assumed where H_i = H_m. The next stage is to let the applied magnetic field change a bit below H_m and a bit above H_m, i.e., introduce the internal DC magnetic field as a variable. For H_i > H_m, the resonance frequency increases and for H_i < H_m, there is a state of undersaturation, i.e., 4πM < 4πMs. At saturation, the third parameter of the Polder tensor, µ_z, has a unit value, i.e., µ_z = 1. When magnetization is below saturation, µ_z ≤ 1. Equation 10 defines µ_z as:

where:

and

for the curve approximation constants A and N.

The results for the Gilbert solution and for the Landau and Lifshitz solution are given in Figs. 12, 13, 14, and 15. No differences were found in the solutions using the original Landau and Lifshitz equation or with Gilbert's approximation. This analysis compared curves for solutions including higher modes, i.e., n = 6 and n = 12, and results were found to be identical. Curves were compared using different ferrite substrates with the same results. In addition, the two critical parameters, |κ/µ| and µ, were examined as functions of frequency, and no major differences were found between the Landau and Lifshitz and Gilbert solutions. A difference was found in the imaginary part of µ, but this approaches zero for the circulator solution and so at any negligible value (less then 0.0003) the difference is of no significance.

Of course, circulator design is complex and has only been briefly explored here. Circulator design involves external and internal applied magnetic fields and their dependence on the resonator disk/cylinder radius-to-height (R/h) ratio. Circulator design also involves impedance matching of the circulator ports to the transmission lines. Impedance matching requires proper selecting the transmission-line media and is dependent on the coupling width-to-height (w/h) relation. The width is related to the coupling angle, 2ψ, through

A circulator design program developed by the author takes these and other factors into account.^8,9

Some minor discrepancies were found in this new approach to circulator design compared to the curves generated by the two classical circulator equations. But, in general, this simpler circulator model provides results comparable to a much more complex circulator model, and without the computational overhead required.

REFERENCES

1. H. Bosma, "On Stripline Y-Circulation at UHF," IEEE Transactions on Microwave Theory & Techniques, Vol. 12, 1964, pp. 61-72.
2. C.E. Fay and R.L. Comstock, "Operation of the Ferrite Junction Circulator," IEEE Transactions on Microwave Theory & Techniques, Vol. 13, 1965, pp. 15-27.
3. Y.S. Wu and F.J. Rosenbaum, "Wideband Operation of Microstrip Circulators," IEEE Journal, Vol. 22, 1974.
4. J. Watkins, "Circulator Resonant Structures in Microstrip," Electron Letters, Vol. 5, 1969, pp. 524- 525.
5. L. Landau and E. Lifshitz, "On the Theory of the Dispersion of Magnetic Permeability in Ferromagnetic Bodies," Physik Z. Sowjetunion, Vol. 8, 1935, p. 153.
6. D. Polder, "On the Theory of Ferromagnetic Resonance," Philosophy Magazine, Vol. 40 40, 1949, pp. 99-115.
7. T.A. Gilbert, Armour Research Foundation Report. No. 11, Armour Research Foundation, Chicago, Illinois, January 25, 1955.
8. Z.M. Harbater, "Wide Band Circulators and Tapers," paper delivered at Symposium of local branch of IEEE Professional Group of Antennas and Microwaves, S-AP/ED/MTT Joint Chapter, 1983.
9. Z. Harbater, "A Mathematical Model for Y-junction Circulator Design," Microwave Journal, Vol. 41, No. 11, November 1998, pp. 58-68.
10. B. Lax and K.J. Button, Microwave Ferrites and Ferrimagnetics, Chap. 4, pp. 145-157, McGraw-Hill, New York, 1962.
11. R.F. Soohoo, Theory and Application of Ferrites, Chap. 5, pp. 59-66, Prentice-Hall, Englewood Cliffs, NJ, 1960.
12. H. Suhl and L.R. Walker, "Topics in Guided Wave Propagation Through Gyromagnetic Media," Bell System Technical Journal, Vol. 33, 1954, pp. 579-659.
13. H. Suhl, "The Nonlinear Behavior of Ferrites at High Microwave Signal Levels," Proceedings of the IRE, October 1956, pp. 1270-83m.
14. J. Helszajn, D.S. James, and W.T. Nisbet, "Circulators using Planar Triangular Resonators," IEEE Transactions on Microwave Theory & Techniques, Vol. 27, 1979, pp. 188-193.
15. J. Helszajn, "Quarter-wave Coupling Junction Circulators using Weakly Magnetized Disk Resonators," IEEE Transactions on Microwave Theory & Techniques, Vol. 30, 1982, pp. 800-806.