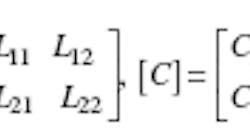Magnetic-resonance-imaging (MRI) systems can produce high-resolution images of cross sections of human bodies, proving to be invaluable for medical diagnostics. An important component in an MRI system is the RF probe used to emit a uniform RF magnetic field over the section of the human body under investigation and needed to receive the magnetic-resonance signals from the body for constructing high-quality images. What follows is an electromagnetic (EM) analysis of one type of probe developed for use in MRI systems.
A number of different types of RF probes have been developed for use in MRI systems and growing interest has focused lately on noncylindrical coils with the final goal of increasing the filling factor and subsequently the signal-to-noise ratio (SNR) of nuclear- magnetic-resonance (NMR) and MRI systems. Elliptical coil1,2 resonators are well suited for clinical applications (e.g., applications involving the wrist or abdomen) but are also appropriate for non-medical samples (e.g., analysis of packaged foods). This type of coil is generally based on birdcage analysis and besides its complex theoretica background, practical implementation of this type of RF probe is difficult.1,2
In ref. 3, a simple and efficient alternative to elliptical birdcage coils based on the slotted-elliptical-tube-resonator (SER) design was presented. Numerical calculations using the finite-element method (FEM) (the effect of the shield has been partially studied) show that the field homogeneity of the slotted-elliptical-tube resonator generally performs as well as noncylindrical birdcage coils, with the advantages of being easier to construct and operate.
The authors conducted an EM analysis of an unloaded slotted elliptical tube resonator (SER) using the method of moments (MoM) in two dimensions.
The analysis allows the determination of the EM parameters: ( and ) matrices taking into account all geometrical parameters of the SER and simulates the frequency response of S11 at the RF port of the designed slotted- elliptical-tube resonator. To demonstrate the SER in an application, the resonator was used as an MRI probe with the SER in an optimum configuration and operating at 300 MHz (proton imaging at 7 T). The resonator has -73.27 dB minimum reflection and unloaded quality factor (Qo) more than 500 at 300 MHz.
Fig. 1a presents a schematic representation of the slotted elliptical-tube resonator. This coil consists of two conductive bands of thickness t carrying opposite currents on each side of a cylinder. The two conductive bands can be mounted on the long (a) or short (b) axes of the ellipse, but the FEM calculations of ref. 3 showed that better homogeneity is obtained if the conductive bands are fixed on the short axis. The conductive sheets are connected at the ends with capacitors to the cylindrical outer shield of radius rb (Fig. 2).
Fig. 1b presents the SER's elliptical cross section. Angle θ is called the "window angle." The optimum value of the window angle depends both on the longto- short axis ratio (a/b) of the ellipse and on the outer radius-to-long axis ratio (rb/a) of the SER.3 For the analyzed SER of ref. 3 with a/b = 1.8 and rb/a = 2.4, the optimum field homogeneity was obtained for a window angle of 72 deg. The EM properties of the shielded and unloaded slotted elliptical tube resonator can be described in terms of its primary parameters, the inductance and capacitance matrices, and , and its secondary parameter, the unloaded quality factor Qo, where:
The inductance matrix contains the self-inductances of the bands on the diagonal, and the mutual inductances between bands in the off-diagonal terms. The capacitance matrix, , accounts for capacitance effects between the two conductive bands, characterizing energy storage in the shielded SER resonator.
The numerical calculations of the primary inductive and capacitive matrices ( and ) of the analyzed resonator were carried out with LINPAR for Windows (Matrix Parameters for Multiconductor Transmission Lines), a two-dimensional (2D) Method of Moments (MoM) software for numerical evaluation of the quasi static matrices for multiconductor transmission lines embedded in piecewise-homogeneous dielectrics.4 The technique used in the program is based on an electrostatic analysis. In the analysis, the dielectrics were replaced by bound charges in a vacuum, and the conducting bodies were replaced by free charges. A set of integral equations was derived for the charge distribution from the boundary conditions for the electrostatic potential and the normal component of the electric field. The MoM was applied to these equations, with a piecewise-constant (pulse) approximation for the total charge density and the Galerkin technique.
When and are found, it is possible to estimate the resonance spectrum (S11) of the resonator shown in Fig. 2 using an adapted numerical model.5
The MRI probe consists of the shielded SER resonator with length l, matching capacitor CM, and terminating capacitors CSi and CLi (i = 1, 2).6
The unloaded quality factor (Qo) of the resonator can be estimated from a reflection (S11) sweep with frequency7:
where:
fr = the resonance frequency;
fu = 3-dB frequency above the resonance frequency; and
fl = the 3-dB frequency below the resonance frequency.
Continued on page 2
Page Title
The MoM approach makes it possible to simulate the performance of a design and decide if a set of constraints can realize the probe. Segmentation of the charged surfaces of the shielded SER using LINPAR is shown in Fig. 3.
Fig. 4, Fig. 5, Fig.6, and Fig. 7 show the influence of the window angle θ on the EM parameters ( and ) of the shielded slotted elliptical tube resonator. The influence of the shield on the EM parameters of the SER is shown in Fig. 8, Fig .9, Fig. 10, and Fig. 11.
The MoM analysis made possible the determination of the EM parameters, with the and matrices taking into account all geometrical parameters of the SER. The obtained curves in this work are essential for the design of MRI probes using the SER.8
For rb/a = 2.4 and θ = 72 deg., the EM parameters of the shielded SER coil are:
Finally, the MRI probe of Fig. 2 was designed with the following features:
a short axis b of 10 cm;
a long-to-short axis ratio (a/b) of 1.8;
an outer radius-tolong axis ratio (rb/a) of 2.4;
a sheet thickness-toshort axis ratio (t/b) of 0.1;
a window angle (θ) of 72 deg.;
a relative dielectric constant (εr) of 1;
a resonator length l of 25 cm;
a matching capacitor CM with value of 20 pF and source and load terminating capacitors, CSi and CLi, both with value of 1 pF.
Fig. 12 shows the simulated frequency response of S11 at the probe's RF port. The frequency response of the probe using the shielded slotted elliptical resonator has a minimum at the chosen resonant frequency, i.e., 300 MHz.
In summary, this article has presented an effective design approach for an MRI probe using a shielded slotted elliptical resonator. To reach the final objective, it was necessary to determine the EM parameters of the shielded SER. In the 150-to-520-MHz frequency band, the numerical calculations were carried out with LINPAR for Windows 2D EM software using the MoM approach which makes possible the determination of the quasistatic matrices ( and ) for the resonator. When the primary inductive and capacitive matrices ( and ) are found, it is possible to estimate the simulated frequency response of S11 at the probe's RF port, then making it possible to evaluate Qo.