Magnetic-resonance-imaging (MRI) systems for medical and scientific applications require a high-performance, high-power inductor capable of establishing a uniformly strong magnetic field. The transverse-electromagnetic (TEM) resonator1 has received a great deal of attention recently as a superior replacement for standard birdcage coils2 in MRI applications requiring magnetic field levels of 4.7 to 9.4 T. For example, at operating frequencies of 200 and 400 MHz,3 a TEM resonator can achieve better magnetic field homogeneity and a higher quality factor (Q) than an equivalent birdcage coil resulting in improved MRI image quality. In support of the analysis and design of a highQ TEM resonator for MRI applications based on coupled microstrip lines, the authors developed an effective approach based on the use of the finite-element method (FEM).
The primary difference between a TEM resonator and a birdcage coil is the cylindrical shield. The shield functions as an active element of the system, providing a return path for currents in the inner conductors. In a birdcage coil, the shield is a separate entity, disconnected from the inner elements, and only reflecting the fields inside the coil to prevent excessive radiation loss. Because of its shield design, a TEM resonator behaves like a longitudinal multiconductor transmission line that can support standing waves at high frequencies.4 Unlike a birdcage coil, the TEM resonator's inner conductors do not possess connections to their closest neighbors, but instead connect directly to the shield through capacitive elements. Resonance mode separation is accomplished though mutual coupling between the inductive inner conductors. Since all the conductors connect to the shield with tunable capacitive elements, the field distribution can be adjusted to achieve the best homogeneity.
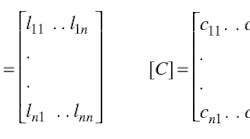
In ref. 5, the authors successfully adapted the numerical tool used in ref. 6 to analyze and design an n-element unloaded coupled-microstrip-line TEM resonator. This adapted numerical tool allows the determination of the primary parameters: the inductive and capacitive matrices, and , respectively, with respect to the geometrical parameters of the TEM resonator by FEM analysis. A comparison of these FEM results with those obtained in ref. 4 by the boundary element method (BEM) show good correlation in the case of a 12-element unloaded coupled-microstrip-line TEM resonator. To demonstrate this adapted numerical method, an eight-element unloaded coupled-microstrip-line TEM resonator will be designed and analyzed. The resonator has –63.33 dB minimum reflection and an unloaded quality factor (Qo) of 400 at 200 MHz.
The unloaded TEM resonator is schematically shown in Fig. 1. The functional elements of the TEM resonator are n inner-coupled microstrip conductors, distributed in a cylindrical pattern and connected at the ends with capacitors to the cylindrical outer shield.4
The cross section of the coupled microstrip line TEM resonator is presented in Fig. 2. It is formed by an outer shield of radius rB and n microstrip conductors w wide and t thick which constitute the cylindrical pattern of radius rR.
The EM properties of the coupled microstrip line TEM resonator can be described in terms of its primary parameters , and its secondary parameter, the unloaded quality factor Qo :
The coefficients for these matrices are obtained by solving a two-dimensional static field problem based on Laplace's equation:4-7
where:
V = 1 V on the ith conductor's surface, and
V = 0 on all others conductors.
In this article, the solution of Eq. 1 is found by using FEM analysis. This solution represents the distribution of potential V at the different mesh nodes of the structure.
Page Title
When potential V is known, it is possible to calculate the ith row of the matrix from the electric charge on each conductor:
where:
lj = the contour around the jth conductor, and
EN = the normal component of the electric field.
Matrix accounts for the capacitative effects between all metallic conductors, characterizing the electric field energy storage in the coupled-microstrip-line TEM resonator.
The inductance matrix contains the self-inductances of the conductors on the diagonal, and the mutual inductances between conductors in the off-diagonal terms. More generally, it defines the magnetic field energy storage. In the high-frequency limit, i.e., the skin depth is sufficiently small such that current flow occurs only on the surface of the conductors, and the inductance matrix can be obtained from the matrix .4-6 The inductance matrix in terms of is:
When the matrices and are determined, it is possible to estimate the resonance spectrum (S11) of the resonator shown in Fig. 3 using an adapted numerical model.8
The MRI resonator developed for this article consists of shielded coupled microstrip lines with length l, matching capacitor CM, and terminating capacitors CSi and CLi (i = 1, n).
The unloaded quality factor (Qo) of the resonator can be estimated from the reflection-parameter (S11) sweep with
frequency:4,6
where:
fr = the resonance frequency of the circuit,
fu = 3-dB frequency above the resonance frequency, and
fl = the 3-dB frequency below the resonance frequency.
The authors applied their modified FEM-based numerical tool to the analysis and design of MRI resonators using coupled microstrip lines. The FEM approach makes it possible to simulate the performance of a design and decide if a given set of constraints makes it possible to realize the resonator.
To design an MRI resonator, the authors analyzed the structure shown in Fig. 2. It has eight inner microstrip conductors and the following set of features:
- An outer cylinder radius (rB) of 52.5 mm
- An inner cylinder radius (rR) of 36.25 mm
- A strip width (w) of 17 mm
- A strip thickness (t) of 0.5 mm
- A dielectric constant (εr) of 1
The FEM approach was employed to solve the potential distribution problem as shown in Fig. 4. Once a solution is obtained, the potential at any point of the TEM resonator can be calculated. Figure 5 shows the resulting potential distributions for different boundary conditions (Table 1).
As discussed above, the integration of the normal flux over the conductor contours determines the per-unit-length parameter matrices. Table 2 lists the first column of the and matrices. This information is sufficient to reconstruct the complete matrices since they are circulant.4-6
Finally, the MRI coupled microstrip line resonator shown in Fig. 3 was designed with the following features: a resonator length, l, of 37.5 cm; a matching capacitor, CM, with value of 19.14 pF, and source and load terminating capacitors, CS and CL, respectively, both with value of 2.415 pF. Figure 6 shows the simulated frequency response of S11 at the RF port of the MRI resonator.
Page Title
The curve presents a minimum at the chosen resonant frequency, i.e., 200 MHz. The obtained minimum of reflection for the coupled microstrip line TEM resonator is very low at the resonance frequency (–63.33 dB). Using Eq. 4, Qo was determined to be equal to 400.
This resulting unloaded quality factor (Qo = 400) obtained from the above geometrical and electrical parameters for the eight-element unloaded coupled microstrip line TEM resonator is very interesting comparing with that recently obtained for the eight-element unloaded coupled coaxial line TEM resonator (with Qo=260).6
This article has presented the analysis and the design of an eight-element unloaded coupled microstrip line TEM resonator for magnetic resonance imaging at 4.7 T (i.e., 200 MHz), which has a high quality factor (Qo = 400). To reach this objective, it was necessary to determine the electromagnetic parameters of the TEM resonator. At 200 MHz the problem is approximated by the resolution of Laplace's equation. Its solution was made by the finite element method, which allows us the determination of the inductance and capacitance matrices ( and matrices, respectively). When the and matrices have been determined, it is possible to simulate the frequency response of S11 at the RF port of the designed TEM resonator. This then makes it possible to evaluate the value of the unload quality factor (Qo) for the MRI resonator.
REFERENCES
- J.T. Vaughan, H.P. Hetherington, J.O. Out, J.W. Pan, and G.M. Pohost, "High frequency volume coils for clinical NMR imaging and spectroscopy," Journal of Magnetic Resonance Medicine, Vol. 32, 1994, pp. 206-218.
- C.E. Hayes, W.A. Edelstein, J.F. Schenck, O.M. Mueller, and M. Eash, "An efficient highly homogeneous radio-frequency coil for whole-body NMR imaging at 1.5 T," Journal of Magnetic Resonance, Vol. 63, 1985, pp. 622-628.
- J.W. Pan, J.T. Vaughan, R.I. Kuzniecky, G.M. Pohost, and H.P. Hetherington, "High resolution neuroimaging at 4.1 T," Journal of Magnetic Resonance Imaging, Vol. 13, 1995, pp. 915-921.
- G. Bogdanov and R. Ludwig, "A Coupled microstrip line transverse electromagnetic resonator model for high-field," Journal of Magnetic Resonance Medicine, Vol. 47, 2002, pp. 579-593.
- N. Ben Ahmed, M. Feham, and M'. Khelif, "Finite element analysis of the transverse electromagnetic birdcage resonator," Revue Afrique Sciences, Vol. 2, No. 1, January 2006, pp. 1-12.
- N. Ben Ahmed, M. Feham, and M'. Khelif, "Analysis and design of a coupled coaxial line TEM resonator for magnetic resonance imaging," Journal of Physics in Medicine and Biology, Vol. 51, April 2006, pp. 2093-2099.
- N. Ben Ahmed and M. Feham, "Design NMR probes at high frequencies," Microwaves & RF, February 2002, pp. 77-103.
- A.R. Djordjevic, M. Bazdar, G. Vitosevic, T. Sarkar, and R.F. Harrington, Scattering Parameters of Microwave Networks with Multiconductor Transmission Lines, Artech House, Norwood, MA, 1990.