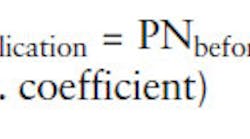Digital microwave radio (DMR) applications require frequency sources with stable outputs and low phase noise. One possible solution is an Xband frequency synthesizer designed for use from 7.7 to 8.2 GHz. It is based on multiplying by three a reliable source operating from 2.56 to 2.74 GHz with outstanding phase-noise performance to achieve final output signals with -84 dBc/Hz phase noise offset 10 kHz from the carrier. The prototype synthesizer features a large tuning voltage range and low operating voltage requirements.
Low phase noise is critical to many wireless systems and radar.1 An X-band frequency synthesizer, for example, in addition to supporting DMR systems, can be multiplied and mixed with local oscillator (LO) signals to cover multiple- frequency applications through 65.6 GHz.2
A variety of synthesizer architectures, such as direct-digital, direct-analog, and indirect-synthesis techniques can be used in modern transceivers, although they each have tradeoffs. Direct-analog synthesizers feature the lowest phase noise with fast switching speed, using mixers to translate the frequencies of surface-acoustic-wave (SAW), coaxial-resonator-oscillator (CRO), dielectric-resonator-oscillator (DRO) and other lower-frequency sources. Unfortunately, direct-analog synthesizers are complex and expensive to design.4 A DDS approach is not suitable for wideband frequency generation since it follows Nyquist criteria, with a maximum frequency that is less than one-half that of the sampling frequency of a digital-to-analog converter (DAC). A DDS provides high frequency resolution and fast switching speed for reasonable cost, but with poor spurious performance.
Phase noise can determine the sensitivity of a receiver in the presence of an adjacent signal. For radar systems susceptible to noise offset 10 kHz from the carrier, the phase noise of a VCO is the dominant source of noise. One way to reduce phase noise is by reducing the bandwidth, although this is not an option for applications requiring wide bandwidths. A divide-by-N module raises the phase noise of the initial frequency source since the signal and noise are both multiplied by N. For optimum phase noise, a synthesizer's loop filter bandwidth must be wide enough to reject VCO noise. Because of the high phase noise from a divide-by-N module, replacing it with a multiplier module can improve phase noise.5 Although frequency resolution will be compromised as a result, fine resolution can be achieved by means of a direct-digital-synthesizer (DDS) module. The inherent high spurious levels of the DDS module can be reduced by means of bandpass filtering.
There are many ways to assemble a wideband frequency synthesizer with phase-lock-loop (PLL) integrated circuits (ICs), narrowband frequency synthesizers, mixers, and multipliers. Mixing and multiplying are the most common methods for designing microwave and millimeter-wave frequency synthesizers not plagued by loop limitations. In a multiplier module, for example, the input frequency is multiplied by an integer coefficient to produce a higher output frequency. Although multiplication results in phase-noise degradation, a typical method of producing high-frequency synthesizers with wide output bandwidths is by multiplying a fixed-frequency or narrowband low-frequency synthesizer. In a mixer frequency-synthesizer structure, the output phase noise will be 3 dB/Hz higher than the highest phase noise of the two mixed modulus sources:
Mixer techniques can also be used to create wideband synthesizers. The input frequency and LO frequency are added and subtracted, with highpass filtering removing spurious products.
Many frequency synthesizers are based on the use of PLLs, where a frequency divider module divides the output frequency by integer 1, as shown in Fig. 1 and Eq. 2:
A PLL synthesizer can generate several frequencies within the bandwidth of the VCO by constant frequency spacings from Freference as explained in ref. 5. A linear model of a PLL synthesizer is a closed-loop system with a number of different phasenoise sources as shown in Fig. 17:
Assuming the loop filter is first order:
Substituting Eq. 4 into Eq. 3 creates:
While the VCO and loop filter are first order, the system is second order.
Figure 2 shows an example of the multiplying technique, where output signals are required from 7.7 to 8.2 GHz with phase noise of -84 dBc/Hz offset 10 kHz from the carrier. With a 3 multiplier, the characteristics calculation is as (7.68 8.20)/3 = 2.56 2.74 GHz with -94 dBc/Hz phase noise required for the 2.56-to-2.74- GHz bandwidth:
The step size of the primary synthesizer is 10 kHz, with the final multiplied step size expressed as:
A PLL frequency synthesizer's building blocks include a reference frequency source, loop filter, phase/frequency detector (PFD), and divide-by- N modules.6 The loop filter is the most critical module since it affects the inband phase noise (from the reference oscillator) and helps eliminate spurious and adjacent harmonic frequencies. The loop filter must also provide adequate control voltage for the VCO. Passive filters provide about 5 V, while active filters support from about 0 to 22 VDC. In the block diagram (Fig. 1), divider N reduces the VCO's frequency to FVCO/N. The PFD detects the difference between an input frequency and the frequency of the VCO (FVCO) divided by integer N (FVCO/N) and, based on the phase or frequency difference, generates a DC voltage to tune the VCO.
In a PLL, the VCO is the dominant source of phase noise (Fig. 3):
To minimize phase noise, the phase detector gain, KPFD, should be maximized to minimize the sensitivity of VCO gain, KVCO8,9:
Flicker noise expresses close-in noise8:
where
F = noise value expression,
K = Boltzmann's constant,
T = environment temperature,
B = bandwidth (usually 1 Hz),
Pavs = the loop output power,
Fc = center frequency,
fm = offset frequency,
1/N = divider ratio,
KPFD = phase detector transfer function,
H(s) = loop filter transfer function, and
KVCO = VCO transfer function represented in Eq. 7.
Continue to page 2
Page Title
Referring to Fig. 1, the transfer functions of the noise sources from reference oscillator to output is
The noise source transfer function of each block responds to the equations above. Each has G(s)/ in common. This is called the in-band noise relation where ?c is the loop bandwidth, fc is the loop phase, and H(s) is the feedback loop gain, 1/N10 :
Note that G(s) has a reverse relation with s or ?c as shown in Fig. 4 and Eq. 22:
To validate these assumptions on phase noise, the Advanced Design System (ADS) software from Agilent Technologies was used to simulate performance at 2.7 GHz (Fig. 5). For further validation, a frequency synthesizer for 2.50 to 3.0 GHz (Fig. 6) was designed using the ADISimPLL software from Analog Devices. The circuit has a model ADF4108 synthesizer integrated circuit (IC), a model OP484 opamp IC from Analog Devices, and model HMX-333-16D VCO IC from Z-Communications (). A model RMK-3-123+ multiplier from Mini-Circuits was used for the integer 3 multiplication. Simulation results show phase noise of -99 dBc/Hz offset 10 kHz from a 2.7-GHz carrier, which agrees with ADISimPLL simulation results in the table. Simulations show the first three spurious frequencies at -46, -67, and -80 dBc, primarily from reference spurs. The step size and loop bandwidth relationship indicates the spur attenuation level. The spacing between the first three spurs is usually equal to the step size or one-half of the channel step size. A step size of 25 kHz and loop bandwidth of 15 kHz were chosen to optimize spurious levels.
REFERENCES
1. M. Moghavvemi and H. Ameri, "Design and fabrication of wideband frequency synthesizer," Report, Faculty of Engineering, University of Malaya, March 2009.
2. M. Moghavvemi and H. Ameri "Assemble A Ku-Band Frequency Synthesizer," Microwaves & RF, January 2009, pp. 80-85.
3. T. Endres, R. Hall et al., "Design and Analysis Methods of a DDS-based Synthesizer for Military Space-Borne Applications," IEEE International Frequency Control Symposium Proceedings, 1994, pp. 625-632.
4. A. Abidi, "Radio-frequency integrated circuits for portable communications," in Proceedings of Custom Integrated Circuits Conference, Vol. 83, No. 4, April 1995, pp. 151-158.
5. Zahid Yaqoob Malik and Mubashar Yasin, "Design and Implementation of an X-Band Frequency Synthesizer for Radar Application," Proceedings of International Bhurban Conference on Applied Sciences & Technology, Islamabad, Pakistan, Jan. 8-11, 2007, pp. 10-14.
6. Alexander Chenakin, "Building a Microwave Synthesizer, Part 1," High Frequency Electronics, May 2008, pp. 58-67.
7. Ulrich L. Rohde, "Parameters extraction for large signal noise models and simulation of noise in large signal circuits like mixers and oscillators," 23rd European Microwave Conference, Madrid, Spain, Sept. 6-9, 1993, pp. 465-470.
8. G. Sauvage, "Phase Noise in Oscillators: A Mathematical Analysis of Leeson's Model," IEEE Transaction on Instrumentation and Measurement, Vol. 26, No. 4, December 1977, pp. 408-410.
9. D. Leeson, "A Simple Model of Feedback Oscillator Noise Spectrum," IEEE Proceeding Letters, Vol. 54, No. 10, February 1966, pp. 329-330.
10. Dean Banerjee, "PLL performance, simulation, and design," 3rd ed., Dog Ear Publishing, pp. 48-50, 2004.