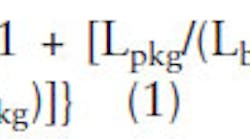Amplifier efficiency is essential not only for mobile devices, but increasingly to conserve power consumption in wireless communications base stations and cell sites. The Class E amplifier in this article produced efficiency of 60 percent from 1.9 to 2.2 GHz using a standard packaged transistor. 1 The techniques used to design and build this amplifier can be employed to design Class E amplifiers at any frequency of interest.
The Class E amplifier has been extensively studied and is relatively easy to implement.2-5 By allowing the drain shunt capacitance to be discharged when the instantaneous RF voltage crosses zero switching losses can potentially be eliminated. This makes 100-percent efficiency theoretically possible, although in practice component tolerances and finite on-resistance of the switching transistor limit efficiency. To explore the limits of the Class E topology, an amplifier using lumped-element matching components was designed based on a 10-W GaAs pHEMT model MRFG35010 packaged transistor from Freescale Semiconductor. It achieves its high performance in part by presenting the correct harmonic terminations2 transformed to the device package plane.
The amplifier's drain efficiency was greater than 74 percent when fabricated on a standard printed-circuit board (PCB) at 2.55 GHzone of the highest efficiencies reported using a packaged transistor at this frequency. The approach was then extended to achieve greater bandwidth and produced average efficiency of 56.8 percent from 1.8 to 2.7 GHz and 60 percent from 1.9 to 2.2 GHz. Classical analysis of the Class E switching amplifier mode was performed in the time domain3,4 using a simplified version of the time-domain analysis5 to obtain the initial Class E design parameters. The analysis was extended to include the package impedances of the transistor, and the harmonic terminations were then determined at 2.5 GHz and realized using discrete components. The broadband design was realized using distributed circuit matching networks with the matching circuit designed to provide optimal harmonic impedances from 1.8 to 2.7 GHz.
The simple circuit for this analysis (Fig. 1) was modeled as an ideal switch in parallel with a capacitance (Cp) consisting of the transistor's output capacitance (Cds) in parallel with capacitance that must be added to obtain the correct switching times for the circuit (that is, to yield zerovoltage switching to reduce switching losses). The output circuit contains a series resonator so that only fundamental current flows in load resistor RL. The optimal load for RL was transformed from 50 Ohms in the design.
The analysis assumes that the switch is either "on" (shorting the output capacitance so all current flows in the switch element) or "off" (an open circuit), and the output capacitance is part of the resonator circuit. As a result, the circuit is characterized by two resonant circuits with different loading or quality factors. Timedomain analysis is performed over a range of switching frequencies and switch conduction angles (a) for a given drain bias on the transistor. A conduction angle of 110 to 120 deg. yields optimum efficiency and power output.5 The analysis also showed that by careful choice of operating frequency, conduction angle, and circuit parameters, all parallel capacitance can be delivered by the output capacitance of the device, eliminating the need for an additional capacitor at its output.
The transistor package was modeled as a T-network equivalent circuit between the device output plane and the circuit. The series inductors represent the bond wires and the package tab, and the shunt capacitor is a parasitic capacitance to ground of the connecting components through the plastic package. With these package components in place, only Cds is shorted when the switch is closed. This difficulty was overcome in the analysis by including the package impedances in the resonant circuit when the switch is closed. When the switch is open, the package components are accommodated as part of drain shunt capacitance Cp.
The transistor output capacitance can be combined with the package equivalent circuit components to produce a transmission matrix between the switch and the Class E amplifier circuit. This transmission matrix is then factored into an effective capacitance (Ceq), and a reduced transmission matrix (Fig. 2)6. Equation 1 is ultimately obtained, which shows that the package parasitics increase the capacitance at the transistor drain:
The equivalent capacitance will always be greater than Cds, and by a suitable choice of operating frequency, drain bias, and conduction angle, the required parallel capacitance for Class E operation can be met by the equivalent shunt capacitance Ceq. The equivalent shunt capacitance presented to the transistor can be tuned with the bond wire.1
In Class E, the instantaneous drain voltage can be more than three times the DC drain bias (Vdd). As the recommended drain bias for the MRFG35010 is +12 VDC, it was derated to +8 VDC. With this bias, a conduction angle of 128 deg. yields optimum efficiency and power output and the total parallel capacitance is 7 pF at 2.5 GHz. This operating frequency was chosen so that Cp = Ceq and no additional external capacitor is required. Other parameters for this fundamental frequency are:
load resistance, RL, of 4 Ohms;
load angle = 51 deg;
resonator formed of Ls = 1 nH and Cs = 4 pF; and
tuning inductance (dL)=0.3157 nH.
The assumption for Class E design is that the current waveform at the drain of the device is created by the applied drive and bias, and the voltage waveform at the drain is created from the interaction of the current components with the frequency-dependent impedance presented at the drain2. At microwave frequencies the number of available harmonic impedances is limited and the self-resonant frequencies of components have an effect on performance. The limited number of harmonics constrains the obtainable efficiency because the overlap of voltage and current waveforms increases as the number of harmonics decreases.
The impedance angle at the harmonics must be 90 deg. to prevent generation of significant power in the harmonics, and this design assumes the presence of fundamental, second, and third harmonics. The impedance to the drain of the device at the fundamental, second, and third harmonics becomes Z1 = R1 +jX1, Z2 = jX2, and Z3 = jX3. From ref. 2, Z1 = (1.526+j1.1064)RL; Z2 = -j2.7233RL; and Z3 = -j1.8155RL. With these terminations and using only three harmonics, the maximum theoretical efficiency is 82 percent.2
Using the above values and ideal passive components for the matching network, a simulation was performed with the nonlinear model for the MRFG35010, which yielded drain efficiency of 81.5 percent and poweradded efficiency of 78 percent at an output power of +37.5 dBm (5.6 W). Gain was more than 12.5 dB.
The next step was to replace ideal components with real component models that include losses and resonances. The harmonic load angles and simulated efficiency for a +25-dBm input is shown in the table as the load network is converted from ideal to real model components. Load angles of about -90 deg. can be maintained with real components, at least at the second (most significant) harmonic. High drain efficiencies can be achieved from the device without modifying the in-package network. The power-added efficiency with this load network is more than 72.5 percent.
Continue to page 2
Page Title
The drain voltage and current waveforms of Fig. 3 are obtained at the drain contact of the nonlinear FET model and include the effects of the drain capacitance, which cannot be deembedded. The waveforms show that the voltage and current generally do not overlap, which indicates a high-efficiency mode. Optimum input match was found from source-pull simulation at +25-dBm drive. Only the fundamental input match was considered.
The amplifier was built on a 30-mil-thick RF printed circuit board (PCB) with dielectric constant of 3.55. Lumped components were initially chosen for highest self-resonant frequency (SRF) for best performance.
However, when tuning the second and third harmonics, careful choice of the component resonant frequency can optimize their harmonic impedances. A comparison between the target impedances and the final tuned impedances for the fundamental, second, and third harmonic frequencies (Fig. 4) shows close agreement with the simulated values.
The tuned half-board was then transferred to the complete amplifier, and drive-up measurements were conducted. The measured drain efficiency is shown in Fig. 5 for a range of gate biases and a drain bias of +8 VDC. The highest efficiency is more than 70 percent for all biases and maximum power of +35 dBm. Efficiency of more than 74 percent was achieved at drain bias of +6 VDC when output power was reduced to +32 dBm. A bandwidth of about 100 MHz was observed (2.45 to 2.55 GHz).
Extending the amplifier to a broadband design was based on a distributed output load network.7 If loading up to the third harmonic is considered, the maximum bandwidth is determined when the third harmonic of the low frequency (fL) is coincident with the second harmonic of the high frequency (fH):
Bandwidth = fH fL
3fL = 2fH (2)
Ideal Class E harmonic load impedances at the internal device drain were calculated for the amplifier's intended range based on the simplified timedomain analysis method. These ideal fundamental and harmonic impedances were then transformed to the external package drain lead through Cds and the package parasitics.
Genesys PCB design software was used to synthesize an initial broadband output matching network topology based on ideal lumped elements (Fig. 6). An equivalent matching network was then implemented in microstrip as a distributed circuit and the line lengths and widths were optimized using an EM simulator to achieve the desired impedances. The frequency responses of the synthesized circuit, optimized distributed circuit, and measured PCB are shown in Fig. 7, and are in good agreement.
REFERENCES
1. J. Wood, "Overview of Class D, Class E, and Class F power amplifiers based on a finite number of harmonics," presented at the Workshop on Transmitter Design for High Power Efficiency, IEEE Radio & Wireless Symposium, Orlando, FL, 2008.
2. F. H. Raab, "Class E, Class C, and Class F Power Amplifiers Based upon a Finite Number of Harmonics," IEEE Trans. Microwave Theory & Techn., Vol. 49, No. 8, 2001, pp. 1462-1468.
3. N. O. Sokal and A. D. Sokal, "Class E A new class of high efficiency tuned single-ended switching power amplifiers," IEEE J. Solid-State Circuits, Vol. 10, No. 3, 1975, pp. 168-176.
4. F. H. Raab, "Idealized Operation of the Class E Tuned Power Amplifier," IEEE Transactions on Circuits & Systems, Vol. 24, No. 12, 1977, pp. 725-735.
5. S. C. Cripps, RF Power Amplifiers for Wireless Communications, Artech House, Norwood, MA, 1999.
6. G. Collins, J. Wood, M. Bokatius, and M. Miller, "A Practical Hybrid Class E Amplifier Design," IEEE Topical Symposium on Power Amplifiers, Orlando, FL, January 2008.
7. J. K. A. Everard and A. J. King, "Broadband power efficient Class E amplifiers with a non-linear CAD model of the active MOS device," Journal of Institute of Electrical & Radio Engineering, Vol. 57, No. 2, 1987, pp. 52-58.