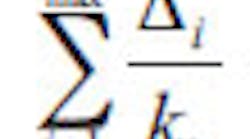Directional couplers are an important part of analog signal processing in microwave systems, including as portions of power dividers and combiners, in directional filters, attenuators, phase shifters, mixers, amplifiers, modulators, and beam-forming networks for antenna arrays.1-19 They are also essential in test applications allowing, for example, measurements of high-power signals with sensitive test equipment by coupling a small sample of the total power. To build on a report begun in this magazine in September 2008, the first part of this two-part article will examine methods for implementing planar directional couplers, which can be fabricated both in discrete forms on printed-circuit boards (PCBs) or as part of monolithic- microwave integrated circuits (MMICs). Next month, Part 2 of this article will explore a tradeoff analysis of different coupler design approaches and how to choose among them to meet a specific set of requirements.
A directional coupler is a reciprocal four-port device. With a signal applied to its input port, it provides two amplitude outputs. It is characterized by a number of parameters, including frequency range, bandwidth, coupling, directivity, isolation, matching, insertion loss, relative phase difference between output signals, phase imbalance, and amplitude imbalance (Fig. 1).
Coupling is calculated as the ratio in decibels of the incident power fed into the input port of the main line of the directional coupler to the coupled port power of the secondary line when all ports are terminated by reflectionless terminations. A 3-dB directional coupler (hybrid network) is a special class of directional couplers in which signals at the two output ports are equal. Its insertion loss is the ratio (in decibels) of input power and output power of the main line with reflectionless terminations connected to ports of the directional coupler. Insertion loss is a combination of coupling loss, conductor loss, dielectric loss, isolation loss, and mismatched loss. Directivity is calculated as the ratio (in decibels) of power of the couple port and the isolated port when all ports are terminated by reflectionless terminations. Isolation is the ratio in decibels of power at an isolated port to available power at the input port. The isolation is equal to the sum of the directivity and coupling.
A directional coupler's relative phase difference can be quadrature (Δφ = 90 deg.) or in-phase/out-of-phase (Δφ = 0 deg. or 180 deg.). A coupler's bandwidth is the range of frequencies for which a parameter falls within a specified limit with respect to certain characteristics. Couplers can be generally separated into narrowband (less than 20 percent) and broadband (greater than 20 percent) designs.
Figure 2 shows a design flow for a planar directional coupler. Defining a system-level specification is the first step in the design flow. This involves system-level requirements applied directly to a directional coupler, as well as derived requirements that depend on the system requirements. Directional couplers specifications include electrical, cost, size, and other requirements. The major parameters that define RF and microwave planar directional couplers are bandwidth, type of directivity, relative output phases (Δf), phase imbalance, coupling (C), amplitude imbalance, insertion loss (IL), matching or return loss (RL), isolation (ISO), integration level, and cost. A coupler's RF specifications include margin for manufacturing tolerances, environmental conditions, and performance degradation over a system's life.
For all requirements, a designer must choose consecutive integer values of weighting coefficients, ki, corresponding to each parameter (the second step of design flow in Fig. 2), from k = 1 for the most important parameter. The maximum value of k can be less than or equal to the number of parameters, depending on whether some parameters are considered to have the same importance or not. Selection of a directional coupler prototype depends on all requirements, and must take into account the corresponding weighting coefficients.
Selecting a directional coupler can be accomplished by using the following procedure:
1. Compare a prototype's normalized parameters, Ppri/Preqi with the normalized requirements, Ppri/Preqi = 1 and determine the deviations, Δi = 1 (Ppri/Preqi) for each prototype, from 1 to n.
2. Choose the weighting coefficients, ki, for each parameter as described above, using k = 1 for the most important parameter (such as insertion loss).
3. Normalize the parameter deviation with respect to the weighting coefficient for each prototype, by means of Δi/ki.
4. Add all the deviation values for each prototype,
5. Compare the sum of the deviations from prototype 1 to prototype n and choose the one with the minimum value of
The final selection of a directional coupler prototype can be made by analysis of a circle diagram.6 The optimum prototype should have the minimum area between real and goal performance.
Synthesizing a planar directional coupler is based on both system requirements and derived requirements. Synthesis results are the physical dimensions of a directional coupler. The analysis of a printed-circuit directional coupler entails definition of the electrical performance resulting from given physical dimensions. An electromagnetic (EM) software simulation may be used to create an S-parameter model of a directional coupler.
Four-port directional couplers symmetrical with respect to one or two planes are frequently implemented in RF and microwave devices. A mirrorreflection method,4,13 is widely used for analyzing symmetrical networks. For RF/microwave couplers, it is popular to analyze directional couplers by means of matrix representations. For analyzing and calculating the dimensions of symmetrical directional couplers, the following approach can be used4:
1. Determine the transfer matrices of the two-port networks (the symmetrical parts of the four-port coupler) with even- and odd-mode excitation. In case of a cascade connection of two-port networks, the transfer matrix is equal to the product of transfer matrices of the component fourport coupler.
2. Determine the most important scattering element of the four-port coupler, for example, coefficient S11, which characterizes the input matching.
Continue to page 2
Page Title
3. Determine relationship among admittances (or impedances) of line segments of the directional coupler under a condition of perfect matching: S11 = 0.
4. Calculate the remaining elements of the scattering matrix, accounting for any discovered relationships among admittances.
5. Determine the characteristics of the four-port coupler.
A directional coupler's parameters can be simulated using a computeraided- engineering (CAE) software program such as the Advanced Design System (ADS) from Agilent Technologies. With a simulation program such as ADS, a designer must set up variable parameters that can be used to optimize the directional coupler. Analysis of manufacturing tolerances should be considered to avoid excessive manufacturing cost. For high-frequency directional couplers this analysis is especially critical.
Planar microwave directional couplers can be designed in a variety of types, including ring directional couplers, branchline directional couplers, and coupled-line directional couplers. In the classical ring or "rat race" coupler with length 3λ/2 (Fig. 3), the spacing between adjacent ports 3 and 4 is 3λ/4; the spacing between all other adjacent ports (3 and 1, 1 and 2, and 2 and 4) is and λ/4. The coupler shown in Fig. 3(b) includes meander quarterwavelength and three-quarter-wave segments to reduce the physical dimensions of the circuit. The 3λ/2 ring coupler has the disadvantage of narrow bandwidth due to the increased length of the 3λ/4 section.
Figure 3(c) shows a modification of the classic coupler, with the 3λ/4 section replaced by a coupled λ/4 line section two diagonal grounded ends and a fixed 180-deg. phase shifter. This hybrid ring configuration provides a one-octave bandwidth compared to the 15-percent bandwidth of the 3λ/4 coupler design. The phase-reversal section can be implemented in different configurations.8
Figure 3(d) illustrates a modified ring coupler using a defected-groundstructure (DGS) design.9 The DGS approach provides for a reduction of coupler size and improved harmonic suppression. The DGS pattern is etched on the ground plane (dashed line) of the microstrip line. This basic DGS is composed of two wide defected areas and a narrow connecting slot, which form the equivalent parallel inductive-capacitive (LC) circuit. The capacitance depends on the etched gap (g) below the conductor line. The length of the connecting slot is the same as the width of the ring. As the etched area of the DGS pattern is increased, the effective series inductance increases. The defected ground of the microstrip line maintains the characteristic impedance of a conventional microstrip line, with the DGS conductor being wider than a conventional microstrip conductor. This is equivalent to increasing the shunt capacitance of the transmission line impedance. Increasing of the equivalent series inductance and shunt capacitance leads to an increase in the phase constant and slow-wave effect. The DGS provides a rejection band in certain ranges due to the incremental increase in the effective inductance of the microstrip line. The ring coupler8 uses six DGS sections Fig. 3(d)> that are embedded in the ring, so that the structure size and the level of the third harmonic can be significantly reduced simultaneously.
The classic branch-line directional coupler Fig. 4(a)> consists of main line 1-3 coupled to secondary line 2-4 by λ/4-long branches spaced by λ/4. Figure 4 shows the different modifications that can be made to a branch-line coupler. The design in Fig. 4(b) includes meander λ/4 segments to reduce the physical size of the coupler. Figure 4(c) shows a dual-band branch-line coupler. 10,11 The two bands are realized by stubs tapped to the center of each λ/4 segment. By changing the absolute and relative length of stubs, different frequency ratios can be realized.
The bandwidth of a branch-line coupler can be increased by increasing the number of branches. For example, Fig. 4(d) shows a three-branch coupler with broad bandwidth. Although additional branches can increase the bandwidth further, couplers with more than four branches are difficult to implement in microstrip because the end branches require difficult-torealize impedances. Figure 4(e) shows a three-branch coupler with power split regulation. The two additional reactive stubs are connected to the center branch. These reactances can be realized as open or short-circuit stubs. If port 1 is the input, the power split between ports 2 and 4 depends on the length of the stubs.
A three-branch directional coupler Fig. 4(d)> can be converted into a lumped-element p network Fig. 4(f)>. For a center frequency, f0, the quarter wavelength segment with characteristic impedance z can be represented by a p-section lumped-element equivalent circuit with series inductance L and two shunt capacitors C with the following values4: L = z/2pf0 and C = 1/2pf0z.
A coupled line directional coupler (Fig. 5) includes two or more coupled lines close enough to each other to be coupled by electrical and magnetic fields. A conventional directional coupler with two coupled lines Fig. 5(a)> is a completely symmetrical four-port network. Perfect matching of this coupler occurs4 when Z0e x Z0o = 1 where Z0e = z0e/z0 and Z0o = z0o/z0 are the normalized impedances for the even and odd modes, respectively; and z0e and z0o are the non-normalized impedances for the even and odd modes, respectively. A fully planar conventional coupled-line coupler Fig. 5(a)> has less than 10 dB coupling due to lower realizable limit of the slot width in print technology. For example, a planar 3-dB microstrip directional coupler has a gap of less than 0.5 mil.
At VHF and UHF, a classic directional coupler Fig. 6(a)> has large dimensions. Figure 5(b) shows a miniature directional coupler4,7 comprised of two coupled lines with short length (less than λ/4). The secondary line output is electrically connected with series inductor L and shunt resistor R. The inductance value depends on the coupling flatness, mid-band frequency, and coupling value. The value of shunt resistor R depends on the impedance of the secondary line and the inductance value. The level of integration of this coupler is approximately five times greater than in other wellknown coupled-line designs.
An original design for a 3-dB coupler was presented by Lange11: an interdigital coupler consisting of several segments of stripline or microstrip line connected to cross wires . The Lange coupler provides tight coupling values with substantially wider gaps than are required for the conventional two-line coupler. It features 3-dB coupling over an octave or more bandwidth. Figure 5(d) illustrates the unfolded Lange coupler with four strips of equal length for simplified circuit modeling.
The bandwidth of a coupled-line directional coupler can be increased by increasing the number of quarter- wave sections. Figure 5(c) shows a three-section directional coupler. The condition for ideal matching is
Z0e1Z0o1 = Z0e2Z0o2 = 1
where
Z0e1 and Z0o1 = the characteristic impedances of the edge sections for the even and odd modes, respectively;
Z0e2 and Z0o2 = the characteristic impedances of the middle section for the even and odd modes, respectively.
The large imbalance between the effective dielectric constant and the related phase velocity for the even and odd modes of the microstrip coupled lines can lead to some limitations in the application of these couplers. Compensation of the differences in phase velocities is achieved by adding lumped-element capacitors in the middle Fig. 5(e)> or at the ends of the coupled section Fig. 5(g)>.4,15 These capacitors do not affect the even-mode signal, but do affect the odd-mode signal, reducing its phase velocity.
Continue to page 3
Page Title
Another directional coupler design uses a sawtooth shape of coupled lines Fig. 5(h)>.14 The sawtooth shape increases the path of odd-mode currents, having a minimum effect on even-mode currents, thereby again leading to a closer matching of phase velocities. An analogous structure utilizes a periodic step shape Fig. 5(i)>. Modifications to conventional coupled- line directional couplers include asymmetric, tapered line, broadside coupled lines, with additional dielectric layers, etc. Fig. 4(a)>.
The performance of the various planar directional couplers already described is compared in Table 1. Figure 6 shows an example of the design flow for the selection of a planar directional coupler prototype. In this example, the requirements include an L-band frequency range, with weighting coefficient of the highest importance at k1 = 1; a 90-deg. relative phase difference, with k2 = 1; 3-dB coupling, with weighting coefficient k3 = 1; 20- percent bandwidth with that having a weighting coefficient k4 = 2; 0.2-dB maximum insertion loss, with weighting coefficient k5 = 3; high directivity, with weighting coefficient k6 = 4; 15 dB isolation, with weighting coefficient k7 = 5; 15 dB return loss, with weighting coefficient k8 = 6; and minimal cost, with weighting coefficient k9 = 7. The selection of a directional coupler prototype starts with satisfying the most critical requirements, with weighting coefficient k1 = k2 = k3 = 1 (step 5.1, 5.2, 5.3), and then the less critical requirements with k4 = 2 (step 5.4), etc. The design flow (Fig. 6) shows that the optimum directional coupler prototype for the above specifications is the three-branch hybrid Fig. 4(d)>.
A design strategy for couplers with printed transmission lines was described in ref. 6. The type of optimal transmission line depends on many different factors including a technology process. According to the directional coupler design flow (Fig. 2), a directional coupler prototype is selected (step 5) after the selection of the transmission line (step 3) and the technology process (step 4). Sometimes the directional coupler prototype with the selected early transmission line does not satisfy requirements because there are some limitations for directional couplers based on different transmission lines (Table 2). In this case, the transmission line should be reselected to satisfy directional coupler requirements.
The selection of a transmission-line technology for a coupled-line directional coupler is critical. As mentioned earlier, a microstrip coupled-line directional coupler has poor directivity due to the difference between the propagation constants for odd and even modes. The advantage of a stripline coupled-line coupler is that the even- and odd-mode phase velocities are equal. In this coupler configuration, stripline offers better directivity and isolation than microstrip.
Next month, this two-part article will conclude with a tradeoff analysis of different coupler types based on required performance specifications. The criteria for analysis include cost versus manufacturing tolerances, cost versus thermal characteristics, cost versus reliabiliy, cost versus loss, bandwidth versus amplitude balance, and various other considerations.
REFERENCES
1. B. M. Oliver, "Directional Electromagnetic Couplers," Proceedings of the IRE, Vol. 42, November 1954, pp. 1686-1692.
2. R. Levy, "Directional Couplers," in L. Young, Ed., Advances in Microwaves, Vol. 1, Academic Press, New York, 1966.
3. G. L. Matthaei, L. Young, and E. M. T. Jones, Microwave Filters, Impedance Matching Networks, and Coupling Structures, Artech House, Dedham, MA, 1980.
4. L. G. Maloratsky, Passive RF & Microwave Integrated Circuits, Elsevier, New York, 2003.
5. L. G. Maloratsky, "Understand the Basics of Microstrip Directional Couplers," Microwaves & RF, February, 2001, pp. 79-94.
6. L. G. Maloratsky, "Design Strategy of RF and Microwave Integrated Circuits," Microwaves & RF, September, 2008.
7. L. G. Maloratsky, "Couplers Shrink HF/VHF/UHF Designs," Microwaves and RF, June 2000, pp. 93, 94, 96.
8. T. Wang and K. Wu, "Size Reduction and Band-Broadening Design Technique of Uniplanar Hybrid Ring Coupler