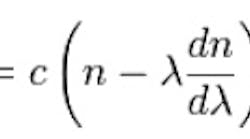Metamaterials and the possibility of negative refraction are interesting, but before industries based on classical and quantum electrodynamics can take them seriously, questions of faster-than-light propagation must be addressed.
A negative value of n is required so that the velocity reverses Snell's Law of refraction, but this cannot be valid with modulus of n < 1 and dispersion curves which indicate that all the velocities are faster than the speed of light (c). How can metamaterials be viable for modulus of refractive index |n| < 1 when the propagation curves indicate Vgroup = Vphase = -3c?
This can be seen where dn/d? = 0 for :-
We now have much literature1,2 with curves that correspond to the profoundly researched anomalous dispersion of Sommerfeld Brillouin- Stratton, (modulus of n < 1 for both positive and negative refractive index n.
How is it possible to have negative refractive index without negative wave impedance (and the implied source of energy)? There are also problems with energy density in classical and quantum electrodynamics.
There are increasing numbers of papers in which scientists claim to have proven extraordinary phenomena by applying the concept of group velocity to the anomalous dispersion of waves. Two of the greatest wave theorists, Arnold Sommerfeld and Lon Brillouin, have dealt with the subject.
In separate papers, Sommerfeld and Brillouin wrote that, in anomalous dispersion, the group velocity cannot be the signal velocity.1 Indeed, in anomalous dispersion, the group velocity goes through both negative and positive infinite values. It also goes through values greater than the speed of light (as does the phase velocity).2
In the anomalous dispersion of Sommerfeld Brillouin- Stratton, the incident wave and resonances interfere to cause apparent speed > c, and/or waves apparently travelling backwards. The published values of +0.9 > n > -0.6 cannot occur, especially where Vgroup = Vphase > c, thus invalidating signal and energy velocity.
References
1. A. Sommerfeld, Annalen der Physik 44, 177 (1914); L. Brillouin, Annalen der Physik 44, 203 (1914). For a lucid English-language digest of the two papers, see ref.
2, p. 334. 2. J. A. Stratton, Electromagnetic Theory, McCheers Publishers.
Dr. Max J. Lazarus
Department of Physics
University of Lancaster,
[email protected]