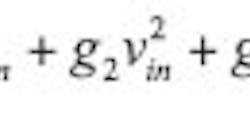Ning Gaoli, Xie Yongjun, and Lei Zhenya
Power amplifiers in modern communications systems must deliver highly linear and efficient operation to properly handle multiple-carrier signals with complex modulation. Typically, a power amplifier (PA) should operate near saturation to achieve high efficiency, although this can also lead to nonlinearity. The nonlinearity generates spectra regrowth, which leads to adjacent-channel interference and violations of wireless standard out-of-band emission requirements. As a result, PAs for wireless communications must be designed with a careful tradeoff between linearity and efficiency.1,2
Numerous linearization approaches have been applied to PAs3-13 to help improve this classic tradeoff, including power backoff, feed-forward and feedback techniques, and predistortion methods, all differing in system architectures and benefits. Among the linearization techniques, analog predistortion is particularly popular for repeater systems since they boost RF signals directly between mobile handsets and cellular base stations. Predistortion methods essentially introduce amplitude and phase distortion at the input of the PA that is equal but opposite to the distortion exhibited by the PA at its output port, effectively cancelling the distortion. For the purposes of this article, the terms predistorter, linearizer, and predistortion circuit all refer to the same thing.
The single-diode based linearizer presented here provides control through bias resistance, with improved performance compared to linearizers based on two anti-parallel diodes. These two-diode linearizers offer limited control since they are only affected by one variablei.e., the bias voltage of the diodes. The single-diode approach is also simpler and more effective than various other novel techniques for PA predistortion. For example, a linearizer developed with microprocessor control of various parameters features effective performance, but it is complex and large in size. A more flexible solution is by generating a PA's required predistortion products with a mixer, applying those products to an attenuator and a phase shifter, then feeding the resulting predistortion products to the input of the nonlinear PA to neutralize its distortion products. This number of components, however, increases the costs and complexity of the predistortion circuitry and sacrifices efficiency.
The single-diode approach is extremely simple, connected with only a resistor and a capacitor. Compared to previous predistorters using a similar approach, neither additional modules (amplifiers, mixers, attenuators, phase shifters, couplers, etc.) nor direct current (DC) bias are needed. The simple single-diode architecture results in a circuit that is extremely compact and cost effective, and provides excellent efficiency in addition to providing good PA linearity.
PAs generally operate under large-signal conditions, where they exhibit the nonlinear transfer characteristics that introduce distortion to their output signals. The distortion consists of amplitude-modulation-to-amplitude-modulation (AM-to-AM) and AM-to-phase-modulation (AM-to-PM) distortion. Figure 1 indicates that as the input signal increases, the magnitude of the gain is compressed, but the phase is also changed. A power (or Taylor) series expansion is often used to explain this phenomenon. However, it appears only AM-AM distortion is included in this technique. To consider AM-AM and AM-PM distortion simultaneously, the generalized power series is employed here. The use of the generalized power series refers to the fact that time delay is incorporated into the coefficient of each term, making the coefficient complex numbers.
The generalized power series applies to a PA with strongly nonlinear behavior. The generalized power series can be used to quantitatively analyze distortion in a nonlinear PA, showing how the distortion is produced and how to mitigate it. The transfer function of a PA operating in the nonlinear region can be expressed as:
where vout = the output signal of the PA; vin = the input signal; and gi(I = 0, 1, 2, ) are the complex coefficients that include magnitude and phase and are related to the specific circuit under analysis. In this case, the magnitude and phase are used to represent the AM-to-AM and AM-to- PM distortion effects, respectively. If the applied input is a single-tone signal, vin = AcosΩit, Eq. 1 can be rewritten as Eq. 2:
This shows that, owing to the nonlinearity, the output signal contains the new DC offset and all harmonic frequency products, in addition to the fundamental frequency signal. The DC offset and harmonics take energy away from the desired signal, thus lowering the PA efficiency and causing output signal distortion.
If the input is a two-tone signal, vin = AcosΩ1t + AcosΩ2t, and this signal representation is substituted into Eq. 1, it will yield a large number of output terms, as shown in Eq. 3:
In this case, there is not only a new DC offset and additional harmonics but also intermodulation distortion (IMD) products. Ordinarily, the coefficients of high-order terms rapidly decrease with the increasing of the order, so they can be ignored. The IMD products produced by the even-order terms are far enough removed from the original two-tone signal in frequency and do not contribute to inband signal distortion (as with harmonics), so only the IMD products generated by the odd-order terms and coincident with the original two-tone signal need be considered. Among these products, the third-order IMD product:
is the most significant for two reasons: (1) it falls in the desired frequency band, making it very close in frequency to the carrier and rendering it unable to be removed by filtering; (2) it is much larger in magnitude than the other in-band IMD products. The third-order IMD product is clearly the main nonlinear source for PAs and has the most deleterious effect on linearity. As a result, the next focus of this study will be on PA third-order IMD products.
Continue on Page 2
Page Title
As the last term of Eq. 3 indicates, the third-order IMD product stems mainly from the third-order term in the transfer function of the PA, since it is just related to the coefficient. This means that to linearize a nonlinear PA, one should mainly eliminate the third-order term. In predistortion techniques, predistorters are cascaded with PAs. They are nonlinear modules that employ nonlinear devices such as diodes and field-effect transistors (FETs), with a transfer function that can be expressed by Eq. 4:
where vo1 = the output signal of the predistorter; vin = the input signal added to the predistorter; ki(i = 0, 1, 2, ) are the coefficients that include magnitude and phase to represent AM-to-AM and AM-to-PM effects, respectively, and are related to the specific predistorer circuit for a specific PA. The transmission characteristic of the PA can then be rewritten as Eq. 5:
where each term has similar meaning as the terms in Eq. 4. Substituting Eq. 4 into Eq. 5 yields the transfer characteristic of the system formed by the combination of the predistorter and the PA. By expanding and arranging the expression, the coefficient of the third-order term is shown in Eq. 6:
It would seem that G3 should be maximized to produce a linear system. Allowing Eq. 6 to go to zero results in Eq. 7:
To suppress the third-order nonlinear distortion at the output, the coefficients of the designed predistortion circuit must meet the condition above. The behavior of the predistorter may be adjusted by means of parameters k1 and k2. Noting that Eq. 7 is a complex equation (including magnitude and phase), to ensure that there always exists a solution, the predistortion circuit must contain at least two independent variables for adjustment, enabling flexible and effective adjustment of the magnitude and phase of the nonlinearity.
The problem of achieving PA linearization has been studied directly, from the point of view of the nonlinear distortion products. It can also be visualized by means of Fig. 2, where it is shown indirectly from the reference point of the fundamental-frequency signal. Figure 3 shows the relationship between the "complex gain" (magnitude and phase) of the fundamental frequency and the input signal. Figure 3(a) depicts the relationship solely for the predistorters, while Fig. 3(b) shows the total performance of the system for the predistorter and the PA. As the input to the PA increases, the nonlinear distortion products rob more energy from the desired signal, and the magnitude of the "complex gain" diminishes. This condition is known as gain compression. At the same time, the phase of the signal is changed as well. Figure 3(a) shows the ideal performance of the predistorteri.e., with gain expansion and phase lagging, the opposite of what is produced at the output of the PA. When combined, the whole system exhibits linear behavior, where the magnitude and phase of the "complex gain" remain constant, as shown in Fig. 3(c).
Based on this analysis, a simple and effective predistortion circuit is proposed in Fig. 4. This simple circuit consists of a diode in series with a resistor and in parallel with a capacitor. The values of resistor R and capacitor C serve as the two independent variables needed for adjustment of magnitude and phase. Based on the distortion characteristics of the PA, either of the parameters can therefore be altered to achieve the desired predistortion characteristics. The circulator connects the predistorter and the PA (Port 2) to be linearized, which is found to improve the return loss at the input (Port 1) effectively as well.
The diode complies with the voltage-current characteristic shown in Eq. 8:
where iD = the current through the diode; vD = the voltage across the diode; IS = the reverse saturation current; and α = a parameter related to the diode's semiconductor process. For the diode presented here, IS and a have both been determined. Suppose that vD is a single-tone signal, represented by Eq. 9:
then iD can be expanded to the Fourier series as shown in Eq. 10:
where In = the Fourier coefficient and can be expressed as shown by Eq. 11:
was to the fundamental frequency, the impedance that the diode presents to the fundamental-frequency signal is represented by Eq. 12:
Continue on Page 3
Page Title
where Zd = the diode impedance and J1(aVL) = a first-order Bessel's function of the first kind. By applying the large argument approximation, when aVL) is large enough, it can be simplified by the approximation of Eq. 13:
Then reflection coefficient {γ} can be obtained by means of an easy derivation, as shown in Eq. 14:
where R and C are two independent variables that make it possible to control the AM-to-AM and AM-to-PM performance of the predistorter flexibly and effectively by varying the values to give the desired output.
To confirm the validity of the proposed predistorter, it can be connected to a PA for study, so as to determine the amount of improvement in linearity that it can yield. The PA can be a typical unit used in a wireless repeater or basestation application. The chosen amplifier operates at 1.9 GHz with output power at 1-dB compression of +43 dBm, and with linearity and efficiency performance levels as shown in Figs. 5 and 6, respectively.
Two-tone testing is an almost universally accepted method of assessing amplifier linearity and can illustrate both amplitude and phase distortion present in an amplifier. For evaluating the experimental single-diode predistorter with this repeater amplifier, a two-tone signal centered at 1.9 GHz with 1-MHz tone spacing was applied to the input of the PA to verify linearity; test results are shown in Fig. 5. It is clear that at +43 dBm output power, the third-order IMD coefficients (IMD3) are about -30 and -33 dBc, corresponding to the lower and upper bands, respectively. Figure 6 shows the dependence of the power-added efficiency (PAE) on the output power. PAE is used in this evaluation since it takes into account both amplification capability as well as power consumption. The PAE is about 35% at +43 dBm output power. This is somewhat low, since the PA is operating under Class A bias conditions for optimum linearity performance.
Now that the performance of the PA alone is well understood, the single-diode predistorter will be added to the amplifier to gauge its improvement in the PA's linearity. The values of R and C were judiciously selected to provide suitable inverse predistortion characteristics so as to minimize the nonlinear distortion at the output of the PA. Similar tests were performed on the amplifier with the predistorter as previously conducted without it, and the results are depicted in Fig. 7 and Fig. 8.
The linearized PA suppresses IMD3 products by about -39.3 and -43.5 dBc corresponding to the lower and upper bands, respectively, at +43-dBm output power (Fig. 7). The analysis of the results clearly shows that an impressive improvement in linearity of nearly 10 dB was achieved owing to the predistorter. In addition, there is an increase in PAE to a certain extentspecifically, 36.8%. This may be explained by minimizing the undesired distortion products (such as intermodulation products and harmonics) and their opportunities to rob power from the desired fundamental-frequency signals.
In summary, the theory detailed here and the tests performed on the simple circuit show the validity of the proposed predistortion circuit. Its simple architecture allows it to be realized cost effectively and compactly. In addition to providing improved PA linearity, it also provides a boost in amplifier PAE.
ACKNOWLEDGMENTS
The authors would like to acknowledge the hardware and software support from the National Key Laboratory of Antennas and Microwave Technology. The authors are also thankful to their colleagues at the Microwave Research Institute for their sincere and great help.
REFERENCES
1. P.B. Kenington, High-Linearity RF Amplifier Design, Artech House, Norwood, MA, 2000.
2. S.C. Cripps, Advanced Techniques in RF Power Amplifier Design, Artech House, Norwood, MA, 2002.
3. M.S. Hashmi, Z.S. Rogojan, and F.M. Ghannouchi, "A flexible dual-inflection point RF predistortion linearizer for microwave power amplifiers," Progress In Electromagnetics Research C, Vol. 13, 2010, pp. 1-18.
4. Y. Shen, B. Hraimel, X. Zhang, G. Cowan, K. Wu, and T. Liu, "A novel analog broadband RF predistortion circuit to linearize electro-absorption modulators in multiband OFDM radio-over-fiber systems," IEEE Transactions on Microwave Theory and Techniques, Vol. 58, No. 11, 2010, pp. 3327-3335.
5. J. Yoon, H. Seo, I. Choi, and B. Kim, "Wideband LNA using a negative gm cell for improvement of linearity and noise figure," Journal of Electromagnetic Waves and Applications, Vol. 24, No. 5, 2010, pp. 619-630.
6. H. Choi, Y. Jeong, J.S. Kenney, and C.D. Kim, "Dual-band feedforward linear power amplifier for digital cellular and IMT-2000 base-station," Microwave & Optical Technology Letters, Vol. 51, No. 4, 2009, pp. 922-926.
7. L. Qiang, Z. Z. Ying, and G. Wei, "Design of a feedback predistortion linear power amplifier," Microwave Journal, Vol. 48, No. 5, 2005, pp. 232-241.
8. S. Yamanouchi, Y. Aoki, K. Kunihiro, T. Hirayama, T. Miyazaki, and H. Hida, "Analysis and design of a dynamic predistorter for WCDMA handset power amplifiers," IEEE Transactions on Microwave Theory & Techniques, Vol. 55, No. 3, 2007, pp. 495-503.
9. Y. Chung and J. Jones, "Si-LDMOS high power amplifier RFIC with integrated analogue predistorter," Electronics Letters, Vol. 44, No. 5, 2008, pp. 361-362.
10. S.C. Bera, R.V. Singh, and V.K. Grag, "Diodebased predistortion linearizer for power amplifier," Electronics Letters, Vol. 44, No. 2, 2008, pp. 125-126.
11. Y. Lee, M. Lee, S. Kam, and Y. Jeong, "A highlinearity wideband power amplifier with cascaded third-order analog predistorters," IEEE Microwave and Wireless Components Letters, Vol. 20, No. 2, 2010, pp. 112-114.
12. H. Park, S. Jung, K. Lim, M. Kim, H. Kim, C. Park, and Y. Yang, "Analysis and design of compact third-order intermodulation generation circuits," Microwave & Optical Technology Letters, Vol. 51, No. 9, 2009, pp. 2137-2140.
13. J. Yi, Y. Yang, M. Park, W. Kang, and B. Kim, "Analog predistortion linearizer for high-power RF amplifiers," IEEE Transactions on Microwave Theory & Techniques, Vol. 48, No. 12, 2000, pp. 2709-2713.