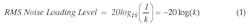Noise power ratio (NPR) has been used to characterize communications systems since the onset of frequency-division-multiplexing (FDM) systems. Traditionally, NPR has been used to test noise and intermodulation distortion (IMD) in 4-kHz voice channels. It is also useful in modern systems for evaluating analog-to-digital converters (ADCs) for wideband applications. It represents a relatively easy ADC test method based on Gaussian noise input to simulate a broadband multitone signal without the need for generating a large number of single-tone sine waves.
In a traditional FDM system, 4-kHz wide voice channels are "stacked" in frequency bins for transmission over coaxial, microwave, or satellite equipment. The number of channels depends on the system. A group is composed of 12 voice channels and occupies a bandwidth of 48 kHz. Similarly, a supergroup has 60 channels and occupies a bandwidth of 240 kHz, and a mastergroup has 300 channels and occupies a bandwidth of approximately 1.3 MHz. Supergroups and mastergroups are often combined to make up even higher capacity systems. For instance, an 1800-channel system occupies a bandwidth of approximately 8 MHz.
At the receiving end, the FDM data is demultiplexed and converted back to 4-kHz individual voiceband channels. The FDM signal is therefore composed of many individual voice channels and passes through amplifiers, repeaters, channel banks, and other components, each contributing noise and distortion. Early studies at Bell Telephone Labs led to the conclusion that the composite signal in an FDM system having more than approximately 100 channels can be approximated by Gaussian noise having a bandwidth equal to the bandwidth of the combined FDM signal.1 For instance, a 1800-channel FDM signal is approximated by Gaussian noise with a bandwidth of 8.2 MHz.
The "quality" of an individual voice channel is then measured by first assuming that there are random "talkers" on all channels except the specific 4-kHz channel under test. An individual 4-kHz channel can therefore be measured for "quietness" using a narrowband notch (band-reject) filter and a specially tuned receiver, which measures the noise power inside the 4-kHz notch (Fig. 1A). With the notch filter out, the RMS noise power of the signal inside the notch is measured by the narrowband receiver. The notch filter is then switched in, and the residual noise inside the notch is measured. The ratio of these two readings (in dB) is the NPR. Several notch frequencies across the noise bandwidth (low, midband, and high) are tested to characterize the system adequately.2
NPR measurements on ADCs are made in a similar manner, except the analog receiver is replaced by a buffer memory and a Fast Fourier Transform (FFT) processor which performs the calculations (Fig 1B). In some cases, the combined FDM signal is converted by an ADC to a digital signal, transmitted, and then converted back to an analog signal using a DAC at the receiver. But the analog method will be considered as the basis for this article.
Work reported by Holbrook and Dixon in 1939 detailed an analysis of FDM systems in an effort to determine the optimum channel "loading" levels for the highest NPR.1 The NPR is plotted as a function of RMS noise level referred to the peak range of the system. For very low noise loading levels, the undesired noise (in nondigital systems) is primarily thermal noise and is independent of the input noise level. Over this region of the curve, a 1-dB increase in noise loading level causes a 1-dB increase in NPR. As the noise loading level is increased, the amplifiers and repeaters in the system begin to overload, creating intermodulation products which raise the system noise floor.3 As the input noise continues to increase, the effects of "overload" noise predominate and the NPR is reduced dramatically. FDM systems are usually operated at a noise loading level a few dB below the point of maximum NPR to allow headroom for peak busy hours. System NPR recommendations for FDM systems were formalized in 1966 by the CCITT/CCIR to measure the transmission characteristics of FDM communications links.2
In a digital system containing an ADC, the noise within the notch is primarily quantization noise when low levels of input noise are applied. However, for very low amplitude signals (less than 1 LSB peak-to-peak), the resulting noise reverts to the input-referred noise of the ADC. For signals that exercise several LSBs of the ADC, the NPR curve is linear, and quantization noise predominates. As the noise level increases, there is a one-for-one correspondence between the noise level and the NPR. At some level, however, "clipping" noise caused by the hard-limiting action of the ADC begins to dominate. This ADC hard-limiting "clipping" noise is somewhat different from the soft-limiting "overload" noise of an analog FDM and results in a "steeper" slope downward in the clipping region.
Much study has been conducted to derive the theoretical NPR of an ideal n-bit ADC.5-7 Reference 6, the most complete, shows the derivation for both uniformly distributed noise and Gaussian noise, although the latter is much more relevant to NPR testing. Since the "clipping" noise component not have a closed-form solution, numerical methods must be used to actually compute the theoretical NPR numbers. Figure 2 offers theoretical NPR values for 10-, 12-, 14-, and 16-b ADCs. The curves are based on an ideal ADC where the only noise is the quantization noise and the clipping noise; real-world values will be lower.
The ADC input range is bipolar, at ±V0 full scale or 2V0 peak to peak. Parameter s is the input RMS noise level while k, which is the noise-loading or crest factor, is defined as V0/s. The value of k is therefore the peak-signal-to-RMS-noise ratio, with k expressed as a numerical ratio. For V0 to represent the peak amplitude, a full-scale sine wave given by v(t) = V0sinvt exactly fills the ADC's input range. The reciprocal of k is the RMS-noise-to-peak-signal ratio, with the RMS noise-loading level defined as 1/k (in dB):
Derivation of theoretical NPR can be broken into two parts. The first step derives the theoretical quantization noise power of an ideal n-bit ADC. The second part derives the "clipping noise" power due to the limiting action of the ADC. The total noise power is the sum of the two noise powers (Fig. 3). This assumes several things. First, the quantization error signal is not correlated to the input signal. This is valid provided the signal amplitude is at least several LSBs in amplitude and the resolution of the ADC is at least 6 b. Second, the sampling rate is twice the input noise bandwidth. Third, the ADC acts as an ideal limiter for out-of-range signals. These three assumptions are valid for most practical systems and lead to a relatively straightforward solution.
Page Title
The quantization noise component (expressed as the square of the actual quantization noise voltage to yield noise power), has been shown to be4
where:
q = the weight of the least significant bit (LSB).
It should be noted that this is the quantization noise power measured over the full Nyquist bandwidth DC to one-half the sampling frequency (fS). If the signal bandwidth is reduced, the noise in the reduced bandwidth is proportionally less, and a correction factor must be added.
Since it is known that q = 2V0/2n, the following can be written from Eq. 2:
However, k = V0/σ, therefore V0 = ks, and substituting for V0 in Eq. 3 yields:
Referring to Fig. 3 for the derivation of the clipping noise power, NC, the clipping noise power can be found from:
and from Fig. 3(b),
and therefore:
where:
P(x) = the Gaussian probability density function (PDF) and is given by:
Substituting V0 = kσ, and combining Eq. 8 with Eq. 7 yields:
The final results of the integration (see Appendix for the complete derivation) yields:
where :
N(k) = the normal distribution function:
For calculation purposes, the function can be approximated by:
The total noise, NT, can now be calculated by adding Eqs. 4 and 10:
The table shows the theoretical peak value of NPR and the corresponding value of k for ADCs with 8 to 20 b resolution. It is important to remember that this is the NPR obtained when the input signal noise occupies the full Nyquist bandwidth, DC to fs/2. For the case of oversampling, where the signal bandwidth, BW, is less than fs/2, the correction factor of 10log10s/(2BW)>, often referred to as processing gain, must be added to the NPR given in Eq. 15:
Page Title
In multichannel high-frequency communication systems, where there is little or no phase correlation between channels, NPR can be used to measure the distortion and noise caused by a large number of individual channels, similar to an FDM system. A notch filter is placed between the noise source and the ADC, and an FFT output is used in place of an analog receiver. The width of the notch filter is set for about 500 kHz to 2 MHz as shown in Fig. 4 for a 12-b 65-MSamples/s AD9229 ADC from Analog Devices (Norwood, MA). The sampling rate is 65 MSamples/s, the notch is centered at 18 MHz, and the NPR is the "depth" of the notch. An ideal ADC will only generate quantization noise inside the notch. However, a practical one has additional noise components due to additional noise and IMD caused by ADC imperfections. Notice that the NPR is about 60.8 dB compared to a theoretical value of 62.7 dB.
Making NPR measurements digitally requires that the FFT have a sufficient number of samples such that there are at least 25 to 50 samples within the filter notch. There are obviously trade-offs between the width of the notch and the FFT size. However, the notch width should not be wider than about 10 percent of the noise bandwidth, or the test results may not be valid.
In the example shown in Fig. 4 for the AD9229, the FFT size was 16,384 which gives a frequency resolution of 65 MSsamples/16,384 = 3.97 kHz. Since the notch filter width is approximately 1 MHz at the bottom of the notch, approximately 250 samples fall within the notch. Due to the specific requirements regarding the center frequency, width, and band-stop rejection, custom-made notch filters are generally required in order to implement NPR tests on ADCs. Achieving good results is difficult using just a simple filter and wideband noise source. Wideband Gaussian noise generators, such as the model DNG7500 from NoiseCom (Parsippany, NJ), are available that allow the user to custom shape the noise according to their application.8 Using a combination of a Gaussian noise shaping generator and notch filter makes this test easier to implement. The results of several FFTs must then be averaged in order to reduce the variation in the NPR results from run to run since there are only a limited number of samples that fall inside the notch itself. The data shown in Fig. 4 represents the average of the NPR results for five individual FFT runs.
NPR should be measured at several different frequencies across the noise bandwidth, thereby requiring several notch filters. Some degradation will occur at the higher frequenciesvery similar to the degradation in other ADC ac specifications such as SNR and SFDR. In many cases, NPR is a good approximation to complicated multi-tone testing and embodies the specific features of many applications when testing your system's dynamic range.7
| References
|