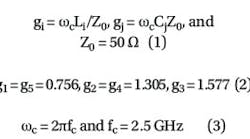Dr. A. Boutejdar, Prof. A. Omar, Prof. E. P. Burte, Dr. R. Mikuta, and Dr. A. Batmanov
DEFECTED GROUND STRUCTURE (DGS) implementations in microstrip can be used not only as tuning elements but to reduce the size of classic passive circuits, including high-low Chebyshev fifth-order lowpass filters. In the case of this lowpass filter design, the DGS acts like a parallel inductive-capacitive (LC) networkthe arrowhead and gap in a triangular-shaped DGS. The trick is to transform a conventional LC network into the equivalent DGS microstrip circuit, in the process achieving a size reduction of 47% compared to a conventional lowpass fi lter design.
DGS have been realized by etching various patterns, such as dumbbell shapes, on the backside metallic ground plane of a printed circuit board (PCB).1-18 The patterns serve to effectively increase the inductance and capacitance of the transmission line, making it possible to represent an LC circuit with an arrowhead-slot DGS (Fig. 1).9-14
Using two low-impedance capacitive sections and three DGS slots instead of conventional high-impedance inductive elements, a fifth-order high-low lowpass filter with Chebyshev response was designed (Fig. 2).18-21 By changing the DGS dimensions, its effective inductance can be modified. The filter was designed for sharp cutoff response and a wide stopband. By using the DGS approach, it can be made much smaller compared to conventional microstrip designs. The DGS filter was modeled, built, and measured, with good agreement between simulated and measured results.
A lowpass filter is typically implemented by all shunt stubs or by series-connected high and low stepped-impedance microstrip line sections.12-24 It can also be realized in stripline by using alternating sections of very high and very low characteristic impedance lines. Stepped-impedance lowpass filters are popular because they can be made smaller than with stub tuning approaches.23 Because of the approximations involved, however, the electrical performance of stepped-impedance lowpass filters is less than ideal, and such filters are usually limited to applications where a sharp cutoff is not required.
Figures 2 and 3 show a high-low stepped-impedance filter layout and its fifth-order Chebyshev equivalent circuit. The inductors in the prototype circuit are realized by transmission lines with width of 0.6 mm (and characteristic impedance of 89 Ω). This width was chosen to simplify filter manufacturing. Capacitors were implemented with wider 5.5-mm transmission- line sections (with characteristic impedance of 23 Ω). Figure 4 offer a comparison between the simulation results for the layout and its equivalent circuit. A lowpass filter with Chebyshev response can be designed with element values defined as follows:
The physical length of the high- and low-impedance lines can be found from Eqs. 4 and 5:
For more precise results, additional capacitors and inductors are included in the equivalent circuit. This introduces modifications to the electrical lengths of the high- and low-impedance lines. The lengths may be corrected by solving Eqs. 7 and 8 by means of the information found from the ABCD matrix presented in Eq. 6 (see equations):
By using the relation between the ABCD matrix, the Z matrix, and the image parameters of the T and II networks, it is possible to solve for the inductor and capacitor values, respectively, portrayed in Eqs. 7 and 8:
The high-low stepped-impedance lowpass filter provides poor rejection-band performance; it is also large, measuring 3.1 cm. Part of the length is due to the use of long thin lines for the inductors. To shrink the design, DGS elements can be used to serve as the inductors. A DGS formed in the ground plane and excited by a 50-Ω line (Fig. 5) behaves like a parallel resonance, and thus can be modeled by means of an LC circuit (Fig. 6). The L and C values are calculated using the relationships in Eqs. 9 and 10 as well as the solutions for the capacitance and inductance values shown in Eqs. 11 through 15:
To characterize an equilateral triangle DGS element, a thin slot of length l = 5.5 mm, width g = 0.5 mm, and triangle side a = 5.5 mm was formed. The variation of the triangle area is used to obtain a certain inductance value. The response for this calibrated structure (Fig. 5) is shown in Fig. 7. Since the simulated response of the DGS agreed closely with that of the equivalent circuit, a calibration chart was created for the DGS to be used for the filter design.
By changing the area of a DGS element, while holding the gap (g) and other dimensions constant, modifications to the arrowhead area lead to an approximate linear variation in inductance and capacitance (Figs. 8 and 9) when the area is larger than 12 mm2. Variation in the inductance, however, is more dominant than that in the capacitance. This variation affects the attenuation pole location, which corresponds to the resonance frequency of the equivalent circuit. The resonant frequency of the equivalent parallel LC circuit becomes lower as the series inductance increases (Fig. 10). After calculating capacitor and inductor values as a function of DGS area, the corresponding impedances can be shown in a curve (Fig. 11), making it possible to directly compute the required DGS area for a desired resonance.
Replacing the transmission-line inductors with DGS elements will shrink the size of the lowpass filter, but also lead to a more complex design (Fig. 12).18 The arrowhead-shaped DGS elements have been shown to have the steepest responses among several DGS shapes. The high-low stepped-impedance lowpass filter was designed for 0.01-dB ripple and a symmetric structure, using three LC resonators in the ground plane and one shunt capacitor on the top circuit layer.
Continue on page 2
Page Title
The filter was designed with a cutoff frequency (Ωc) of 2.5 GHz and resonant frequency at about 5.5 GHz. It was fabricated on a PCB with relative dielectric constant (er) of 3.38 and thickness (h) of 0.813 mm. The dimensions are summarized in the table (and Fig. 3). To replace the arrowhead slots of Fig. 5, the equivalence of Fig. 6 should be satisfied at cutoff frequency Ωc. As a result, the reactance values XLC and XL must be equal (Eq. 9).
The values for the capacitance and inductance of the equivalent circuit were not separately computed. Rather, the impedance XLC and inductance corrections ΩcLc were computed at the same time, using Eqs. 14 and 15, allowing values for the DGS arrowhead area to be found from simple reading of the curve generated by those equations (and shown in Fig. 11). Figures 13 and 14 compare the circuit configurations for the conventional high-low- impedance lowpass filter and the equivalent circuit of the new DGS-based multilayer filter approach, respectively. Equations 16 and 17 were used to calculate the corrected equivalent impedances of the DGS elements needed to design a compact lowpass filter with satisfactory results.
A DGS-based lowpass filter can be designed by following a few steps, starting with calculating the length of the wide microstrip line needed for the required capacitance in the filter circuit. This can be done by applying Eq. 18.
There is also an equivalent inductance of this microstrip line, which can be found by applying Eq. 19.
To determine the required areas of the DGS triangles, Eqs. 20-23 can be applied.
Equation 5 has shown the equivalent capacitance (C) of a transmission line with characteristic impedance ZC and length lC. But there is also equivalent inductance to the transmission line, expressed as LC in Eq. 19. Length lC , which corresponds to 1.661 pF at a resonant frequency of 2.5 GHz, equals 7.7 mm for a 5.5-mm-wide microstrip line. The equivalent inductance for a 7.16-mm long microstrip line is 0.49 nH. In these calculations, length lC is taken as the shortest distance between two neighboring arrowhead shapes.
Dimensions λgC and λgL equal 70 mm and 76.13 mm, respectively, in these calculations. Due to the effects of the DGS elements on the capacitance of the microstrip line, however, the length of the microstrip line had to be changed to maintain the cutoff frequency at 2.5 GHz. The final resonator dimensions are shown in the table, with simulations of the circuit's response in Fig. 15.
The DGS elements were used to design and fabricate a compact microwave lowpass filter (Fig. 16), which was found to have insertion loss of less than 1.5 dB from DC to 2.8 GHz and passband return loss of better than 20 dB (Fig. 17). The filter achieved more than 20 dB stopband rejection at frequencies from 4.4 to 8.7 GHz. The sharpness factor, f0/fc, determines the sharpness of the transition from the filter's passband region to its stopband region. The sharpest theoretical transition is f0/fc = 1. With a sharpness factor of f0/fc = 1.6 for the DGS filter compared to a sharpness factor of f0/fc = 2.14 for a conventional high-low-impedance lowpass filter, the DGS technology appears to offer a great deal of promise in terms of achieving sharp transitions between the two filter operating regions. The proposed filter exhibits sharp cutoff performance, dropping from less than 0.5 dB loss to almost 48 dB signal rejection within a frequency range of only 2.5 GHz. The filter provides spuriousfree performance through 10 GHz and measures 40 x 15 mm.
In an effort to further reduce the size of the filter, the center DGS element from the initial single-layer filter design was moved to another layer in a multilayer circuit construction, while maintaining the same cutoff and resonant frequencies (Fig. 18). The S-parameters for the single-layer versus the multilayer DGS filters are the same from DC to the cutoff frequency, and the rejection is better than 20 dB in the stopband for both filter fabrication approaches (Fig. 19). The size of the multilayer DGS filter, however, is about one-half that of the single-layer DGS lowpass filter. In shifting the middle DGS element to an upper circuit layer, the capacitance of the top circuit layer increases. To compensate for this shift in capacitance, the width of the top-layer microstrip line must be reduced.
Figures 20(a) and 20(b) show the current density distributions in the passband and in the stopband, respectively. The passband response was measured at 1.5 GHz. Since power is fully transmitted between the input and the output, the filter loss is zero. In the filter stopband , the power is fully reflected so that the plot shows infinite loss (or attenuation) in the stopband.
Continue on page 3
Page Title
DGS elements have been shown to provide a means of shrinking the size of passive circuits, such as lowpass filters. The key is determining the size (area) of a selected DGS shape by correlating its area to the equivalent-circuit inductance and capacitance required for a particular filter design as might otherwise be realized by conventional microstrip lines. In addition to smaller size, the DGS elements can deliver even sharper filter cutoffs than conventional microstrip and stripline technologies, and can be used creatively in multilayer filter architectures for further savings in circuit real estate
ACKNOWLEGMENTS
The authors are grateful to administrator Mr. D. Winkler for his computer assistance and Rodieck and Dempewolf, the laboratory managers at the Institute for Electronics, Signal Processing, and Communication (IESK) at the University of Magdeburg, Germany.
REFRENCES
1. D. Ahn, J. S. Park, C. S. Kim, J. Kim, Y. Qian, and T. Itoh, "A design of the lowpass filter using the novel microstrip defected ground structure," IEEE Transactions on Microwave Theory & Techniques, Vol. 49, No. 1, January 2001, pp. 8693.
2. A. Rahman, A. K. Verma, A. Boutejdar and A. S.Omar, "Control of bandstop response of Hi-Lo microstrip lowpass filter using slot in ground plane," IEEE Transactions on Microwave Theory & Techniques, Vol. 52, 2004, pp. 1008-1013.
3. Jia-Sheng Hong and M. J. Lancaster, Microstrip Filters for RF/Microwave Applications, Wiley, New York, 2001.
4. Hsieh and K. Chang, "Compact lowpass filter using stepped impedance hairpin resonator" Electron Letters, Vol. 37, No. 14, July 2000, pp. 899-900.
5. A. Boutejdar A. Elsherbini, and L. Haiwen et al., "Improvement of microstrip low pass filters' characteristics using an optimized number of new multi-ring defected ground structures," Microwave and Optical Technology Letters, Vol. 49, No. 12, December 2007, pp. 3074-3078.
6. J. S. Won, "Microstrip tapped-line filter design," IEEE Transactions on Microwave Theory & Techniques, Vol. MTT-27, January 1979, pp. 44-50.
7. C. S. Kim, J. S. Park, D. Ahn, and J. B. Lim, "A novel 1D periodic defected ground structure for planar circuits," IEEE Microwave Guided Wave Letters, Vol. 10, No. 4, April 2000, pp. 131133.
8. AWR Microwave Office electromagnetic simulation software, www.awrcorp.com.
9. J. I. Park, C. S. Kim, J. Kim, J. S. Park, Y. Qian, D. Ahn, and T. Itoh, "Modeling of a photonic bandgap and its application for the low-pass filter design," in Asia-Pacific Microwave Conference (APMC) 1999 Symposium Digest, pp. 331334.
10. J . S. Lim, C. S. Kim, Y. T. Lee, D. Ahn, and S. Nam, "A new type of low pass filter with defected ground structure," in Proceedings of the 32nd European Microwave Conference, September 2002, pp. 3236.
11. A. Boutejdar, S. Amari, and A. Omar, "A Novel Compact J-Admittance Inverter-Coupled Microstrip Bandpass Filter Using Arrowhead-Shape As Defected Ground Structure," Microwave and Optical Technology Letters, Vol. 52, No. 1, January 2010, pp. 34-38.
12. A. Boutejdar A, A. Elsherbini, and A. Omar, "Method for widening the reject-band in low-pass/ band-pass filters by employing coupled C-shaped defected ground structure," IET Microwave Antennas & Propagation, Vol. 2, No. 8, December 2008, pp. 759-765.
13. T. Kim and C. Seo, "A novel photonic bandgap structure for low-pass filter of wide stop-band," IEEE Microwave Guided Wave Letters, Vol. 10, No. 1, January 2000, pp. 1315.
14. A. Boutejdar, M. Makkey, A. Elsherbini et al., "Design of compact stop-band extended microstrip low-pass filters by employing mutual-coupled square-shaped defected ground structures," Microwave and Optical Technology Letters, Vol. 50, No. 4, April 2008, pp. 1107-1111.
15. G. L. Matthaei, L. Young, and E. M. T. Jones, Microwave Filters, Impedance Matching Networks and Coupling Structures, Artech House, Norwood, MA, 1980, pp. 217228.
16. A. Boutejdar, "Design of A New Compact Dual- Mode Multi-Band Bandpass Filter Using Multi-Armed Ring-Open-Loop Resonators Without Coupling Gaps," Microwave and Optical Technology Letters, Vol. 52, No. 12, December 2010, pp. 2668-2672.
17. D. M. Pozar, Microwave Engineering, Addison- Wesley, Reading, MA, 1990, pp. 486517.
18. Ahmed. Boutejdar, G. Nadim, S. Amari, and A.S. Omar, "Control of bandstop response of cascaded microstrip Low-pass-bandstop filters using arrowhead slots in backside metallic ground plane," IEEE Antennas and Propagation Society (AP-S) Symposium, Washington, DC, 2005.
19. Y. Qian, F. Yang, and T. Itoh, "Characteristics of microstrip lines in a uniplanar compact PBG ground plane," in AsiaPacific Microwave Conference 1998 Technical Digest, pp. 589592.
20. A. Boutejdar, A. Adel Rahman, A. Batmanov, A. S. Omar, and E. Burte, "Miniaturized Band-Stop Filter Based on Multilayer Technique and New Coupled Octagonal Defected Ground Structure (DGS) With Interdigital Capacitor," Microwave and Optical Technology Letters, Vol. 52, No. 3, March 2010, pp. 510-514.
21. A. Boutejdar, A. Batmanov, A. S. Omar, and E. Burte, "A miniature 3.1 GHz microstrip bandpass filter with suppression of spurious harmonics using multilayer technique and defected ground structure open-loop ring," (book chapter in) Ultrawideband, Short-Pulse Electromagnetics 9, Springer, New York, 2010.
22. Jong-Sik Lim and Chl-Soo Kim, "Design of lowpass filters using defected ground structure and compensated microstrip line," Electronics Letters, Vol. 38, No. 22, 2002, pp. 1357-1358.
23. A. Boutejdar, A. Batmanov, E. Burte, and A. S. Omar, "Design of a New Bandpass Filter with Sharp Transition Band Using U-Defected Ground Structure (DGS) and Multilayer-Technique," IET Microwave, Antennas and Propagation, Vol. 4, No. 9,September 2010, pp. 1415-1420.
24. J. S. Park, J. H. Kim, J. H. Lee, S. H. Kim, and S. H. Myung, "A novel equivalent circuit and modeling method for defected ground structure and its applications to optimization of a DGS Lowpass filter," IEEE MTT-S International Microwave Symposium Digest, 2002, pp. 417-410.