This file type includes high resolution graphics and schematics when applicable.
Many passive multiport devices—such as power dividers/combiners, baluns, hybrids, and impedance transformers—rely on electromagnetic (EM) coupling for their intended functions. In the microwave range, the coupling is typically achieved through a capacitive (electrical) interaction between closely spaced transmission lines. With this coupling mechanism the broadest available bandwidth is achieved when the length of the coupling section approaches quarter of the wavelength. Consequently, as the frequency drops below the microwave range, the size of devices utilizing this coupling mechanism grows prohibitively large.
A viable alternative to the capacitive coupling in the RF range is the inductive coupling realized through a mutual magnetic interaction of the wire loops coupled together through a common ferrite core. With a proper selection of ferrite material, core dimensions, and the number of loop turns, device functionality can be significantly expanded toward the lower frequencies. Eventually, the use of ferrite transformers and magnetic coupling results in much smaller broadband devices which manifest better electrical performance because of their reduced ohmic losses.
Some applications, however, call for even broader devices operating in a frequency range covering both RF and microwave bands. But there is a fundamental conceptual difference in designing devices intended for use at RF and at microwave bands. The “lumped-element” approach is a prevalent design ideology at RF, while “distributed elements” and “transmission lines” dominate design approaches at microwave frequencies. There are certain limits as to how far each of these approaches can be stretched into the neighboring band.
More promising is the synthetic approach which combines both concepts into a single device. This approach was particularly successful in developing the ultrabroadband ferrite power dividers and couplers which combine capacitive coupled transmission lines, such as twisted bifilar wires and coaxial lines, with ferrite transformers to add magnetic coupling into the mix.1 Such a hybrid approach could potentially accomodate almost four decades’ worth of bandwidth in a single device.
To assess the suitability of ferrite material for transformer core applications, one should understand the response of nonmagnetized ferrite to an external AC magnetic field. In the absence of DC magnetic bias, the dynamic magnetic response of soft ferrite materials to an AC field is almost completely determined by the effective field of magnetocrystalline anisotropy, HA, which is present in all types of ferrites. This internal field enforces preferential alignment of magnetic moments along some particular crystallographic directions. The random orientation of grains in polycrystalline structures, such as ceramic ferrites, averages this effect and leads to isotropic complex dynamic permeability given by the following relationship:2
μ′i = 1/3 + (2/3){[(HA + 4πM0 + jωG)2 - (ωγ)2]/[(HA + jωG)2 – (ω/γ)2]} = μ′i + jμ″i (1)
where:
4πM0 = the magnetization of saturation, and
G = the dissipation factor which describes dynamic losses in ferrite material.
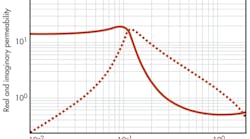
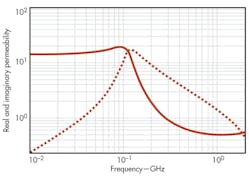
The real part of magnetic permeability, μ′i, further referred to as the initial magnetic permeability, characterizes the capacity of ferrite core to carry a magnetic flux. The imaginary part, μ″i, describes the magnitude of active losses in the wires which are magnetically coupled with ferrite core. Equation 1 describes the broadband frequency response including also the “natural magnetic resonance,” which takes place when the frequency of the AC field approaches the frequency of the spin precession in the internal field of anisotropy, ωA = γHA. Figure 1 shows a typical dispersion of the real (solid line) and imaginary (dashed line) permeabilities resulting from Eq. 1.
Because of significant losses associated with a nonmagnetized ferrite material, the resonance is very broad. One can see that the initial permeability remains almost flat to the resonance. After the resonance, it changes into a rapidly descending slope. As for the imaginary part, the loss gradually grows to reach a maximum at resonance and then slowly decreases with frequency. One very important observation is that the magnetic loss extends far into the microwave range, whereas the initial permeability reduces to the vacuum permeability almost immediately above the resonance.
The very same magnetocrystalline anisotropy which causes the “natural magnetic resonance” has an adverse effect on the magnitude of initial permeability:
μ′i = 2MS/3HA (2)
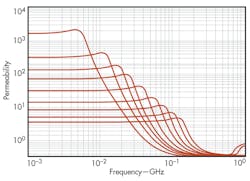
As a result, the ferrites with stronger anisotropy provide broader bandwidth but less permeability and vice versa. This correlation is clearly seen in Fig. 2, which shows a comparative permeability for a group of soft ferrites with various strengths of anisotropy field. The analytical relation which describes the correlation between the bandwidth and magnitude of permeability, known as Snoek’s law, is shown in the same graph.
This file type includes high resolution graphics and schematics when applicable.
Transformer Takeaways
This file type includes high resolution graphics and schematics when applicable.
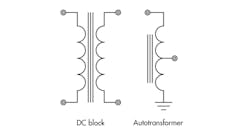
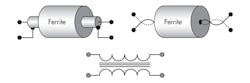
A ferrite transformer is a passive device which transforms the input voltage (impedance, current) into another desired output value. Depending on the connection schematics, it can also provide some other useful functions, such as the DC isolation between input and output, rejection of common mode, and conversion of the balanced impedance to the unbalanced value. In an actual implementation, the RF transformer consists of a closed-loop ferrite core which accommodates two or more windings. Driving a current into one of the windings, referred to as a primary, creates the AC magnetic flux which induces the current in the secondary windings. Some typical transformer configurations are shown in Fig. 3.
If properly designed, the ferrite transformer is practically a lossless device: W1 ≈ W2. To achieve a maximum power transfer from the input to output, the load impedances should match to the input impedance. Assuming that the numbers of turns in the primary and secondary windings are given as N1 and N2, the following relations hold:
n = N2/N1
V2 = nV1
I2 = I1/n
Z2 = n2Z1
For example, if the transformer is used as a two-way power divider, then both output windings should have N2 = N1/(2)0.5 and the output impedances will be Z2 = Z1/2. If necessary, the output impedances can be reinstated to their original values by using up-transformation in the subsequent stage.
The above equations establish only the relative relationships. The actual values are evaluated based on the power rating and bandwidth requirements. The low-frequency cutoff is determined by the falloff of reactance at primary winding. The improvement of low-frequency reactance can be achieved by a variety of ways which include utilizing a higher permeability ferrite, increasing the size of ferrite core, or increasing the number of turns.
Generally all these low frequency improvements come with a price of degrading the high-frequency response. However, with an appropriately selected ferrite core, the resulting reduction in the number of turns can also lead to significant improvement of the high frequency performance, too. In the conventional transformers discussed here the power to the secondary winding is transferred entirely through a magnetic flux within the core. Therefore, the determination on a core cross-section should be made based on the power handling criteria to avoid the nonlinearities and magnetic saturation.
As for the bandwidth characteristics, its high frequency rollover is determined mainly by the Snoek’s limit for the real permeability, which is usually below 200 MHz.
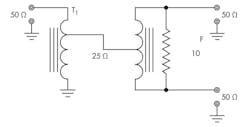
The typical schematic diagram for a two-way power divider realized with conventional transformers is shown in Fig. 4.
In this particular implementation, the first stage is realized with auto transformer having transformation ratio of 1:1/(2)0.5, which results in the output impedance of 25 Ω. The next stage is an isolation transformer with 1:2 ratio which brings two outputs back to 50 Ω unbalanced impedances.
The concept of transmission-line transformers was first introduced by Guanella in 1944. In its basic implementation, the transformer consists of a section of transmission line, such as coaxial cable or twisted bifilar magnetic wire, which is inductively coupled with the ferrite core. Along with coaxial cables, the evenly twisted bifilar magnetic wires are known to maintain consistent in-lane capacity and exhibit transmission-line properties in a broad range of frequencies up to the microwaves with characteristic impedance depending on the wire gauge, insulation thickness and twisting pitch.3
Whereas a coaxial cable is used, the shield acts as a second transmission line which is capacitively coupled with the central wire and provides the path for return current. The best performance is achieved when the line characteristic impedance is equal to the geometrical mean of the source and load impedances. Some configurations for transmission-line transformers, along with their schematic representation, are depicted in Fig. 5.
As in any coupled-line arrangement, the signal propagation in a transformer can be reduced to two different propagation types: even and odd modes. The most fundamental property of a transmission-line transformer is that it responds differently to these modes. In the odd propagation mode the overall magnetic field created by equal and opposite currents in individual wires is cancelled. So, ideally, the presence of ferrite core has no effect on the odd mode. In contrast, the current in the even mode flows in the same direction, thus generating substantial magnetic field within the ferrite core. The purpose of a transmission-line transformer is to act as a choke which suppresses the even mode. In this capacity both the real and imaginary parts of permeability are relevant and useful for the transmission-line transformer. The first one contributes by reflecting the even mode back to the source, and the second by converting the power of even mode into the heat. This is in a clear contrast with the conventional transformer which utilizes only the real permeability to realize its function.
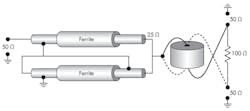
Because of the contribution of imaginary magnetic permeability, the operation of the transmission-line transformer can be extended well into the microwave range. With the even mode almost completely eliminated the transmission line transformer acts as a balun transforming the unbalanced input into a balanced output. Depending on the connection schematics, it can also realize important function of impedance transformation and phase inversion.4 An example of three coaxial 35 Ω impedance transformers arranged to act as a 2:1 balun is shown in Fig. 6 along with the equivalent schematic seen from the input and the output port.
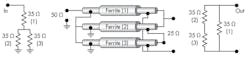
Regarding the power dividers, Fig. 7 shows one of the possible arrangements of transmission-line transformers to achieve a two-way equal power splitting.5 Again, the first stage is realized as 2:1 coaxial balun which is followed by a wire wound isolation transformer to maintain all ports at the level of unbalanced 50-Ω impedances. Figure 7 shows the actual schematic diagrams of TRM’s catalog part DL-208F which fits into a small package size (1 x 1.25 x 0.5 in.) and operates in a very broad frequency range of 20 to 2000 MHz.5
Dr. Karen Kocharyan, Senior RF/Microwave Engineer
TRM Microwave, 280 South River Rd., Bedford, NH 03110; (603) 627-6000, FAX: (603) 627-6025.
References
1. J. Walker, D. Myer, F. Raab, and C. Trask, Eds., Classical Works in RF Engineering, Artech House, Boston, 1974.
2. E. Schlomann, “Microwave Permeability of Partially Magnetized Ferrites,” Journal of Applied Physics, Vol. 41, No. 1, 1970, pp. 204-214.
3. P. Lefferson, “Twisted Magnetic Wire Transmission Line,” IEEE Transactions on Parts, Hybrids, and Packaging, Vol. PHP-7, No. 4, December 1971, pp. 148-154.
4. A. Grebennikov, “Power Combiners, Impedance Transformers and Directional Couplers,” High Frequency Electronics, Vol. 6, No. 12, December 2007, pp. 20-38.
This file type includes high resolution graphics and schematics when applicable.