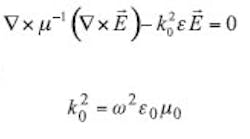High-power test systems often rely on passive components for directing the flow of test signals. One such component is the rectangular waveguide to high-power overmoded circular waveguide mode converter. To optimize the performance of this type of waveguide mode converter, a full-wave electromagnetic (EM) analysis was performed on the N-port waveguide junction of the component. This analysis led to the development of a model by which it was possible to calculate the reflection coefficient of the mode converter as a means of optimizing its performance. In order to validate the model and analysis method, a rectangular waveguide to high-power overmoded circular waveguide mode converter was designed and fabricated for X-band use, with extremely low reflection, small size, and optimized vertical E-field polarization. The measured performance of the X-band prototype compared closely with the performance predictions provided by computer simulations.
High-power-microwave (HPM) signals are typically defined as exceeding 100 MW in peak power at frequencies from 1 to 300 GHz.1-3 With the growth of pulsed-based signals, more and more HPM applications have appeared,4,5 including in HPM directed energy weapons, high-power radar, and microwavedriven plasma heating systems. The dominant operation mode of the sources is the transverse electromagnetic (TE) TE10 mode of rectangular waveguide, but multimode horn antennas6-8 require the TE11 mode of circular waveguide, calling for a mode adapter in some systems. The mode converter9 is needed between the high-power source and the antenna to convert the TE10 mode to a TE11 mode, typically in HPM test systems.
For improved signal transmission and reduced return loss, overmoded waveguide10,11 are often used in high-power microwave systems. A mode converter is needed for systems employing both rectangular and circular waveguide. But, because not only the dominant mode but other modes can be transmitted by the overmoded circular waveguide, designing the rectangular-to-circular-waveguide mode converter is not a simple task.
For this article, a full-wave analysis model of an N-port waveguide junction for the mode converter was built via the finite-element method. then, the reflection coefficient of the mode converter was calculated. Finally, an optimization design method was developed. the optimization method was then applied to design and fabricate a rectangular waveguide to high-power overmoded circular waveguide mode converter, with its measured performance matching quite closely with the simulated performance from the model.
A rectangular waveguide to high-power overmoded circular waveguide mode converter is a kind of two-port waveguide junction (Fig. 1). the junction may be connected with rectangular waveguides or may be loaded with arbitrarily shaped dielectric material. here the boundary plane Γ i connects the discontinuity region Ω to the rectangular waveguide port i (where i = 1, 2 N), and the region Ω surrounded by Γ 1, Γ 2, Γ N, and
S enclosed the waveguide discontinuities completely. S is assumed to be a perfectly conducting wall.
From Maxwell's equations, the following vectorial wave equation is derived with respect to the electric field E:
and e = absolute permittivity and = absolute permeability.
The problem defined by Eq. 1 may be formulated variationally12,13 and the function F(E) expressed by Eq. 3:
where:
∫∫∫Ω dΩ = the volume integral in the region Ω;
∫∫Γ dΓ = the surface integral over the boundary Γ ( = Γ1 + Γ2 + + ΓN + S);
n = the outward unit normal vector on the boundary Γ; and
* indicates the complex conjugate.
By modal expansion, the tangential fields in the waveguide region can be expressed as:
where:
= the tangential field distribution of the nth mode;
Γn = the complex propagation constant;
ain = the given modal amplitude of incident wave; and
arn = the unknown modal amplitude of the reflected wave.
When the finite-element method12-15 is applied to Eqs. 3, 4, and 5, a matrix equation can be obtained. The modal amplitude of the reflected wave can be obtained by solving the matrix equation. The reflection coefficient of the mode converter can be accurately calculated by means of numerical simulation software based on the finite-element method, such as the High-Frequency Structure Simulator (HFSS) EM simulation software from ANSYS.
Figure 2 shows the configuration of the rectangular-waveguide-to-circular-waveguide mode converter, where a and b are the dimensions of the rectangular waveguide, L is the length of the transition segment in the axis direction, and R and d are the radius and length of the straight circular waveguide, respectively. This type of converter can transform the dominant transmission mode (TE10) of the rectangular waveguide (TE10) to the dominant transmission mode of circular waveguide (TE11) by gradually transforming the rectangular waveguide into circular waveguide.
The optimization method for the waveguide mode converter is straightforward. It involves finding the best value for L and adjusting the size of d to obtain vertical E-field polarization in the waveguide port (N). By following this simple optimization method, a rectangular waveguide to high-power overmoded circular waveguide mode converter was designed for use at 8.4 GHz. The dimensions of the mode converter are a = 40 mm, b = 16 mm, R = 25 mm, and d = 9.5 mm.
Page Title
Figure 3 shows how the reflection of the mode converter varies with the value of L. When L is 95.5 mm, the reflection of the mode converter is at a minimum, with the reflection values rising as the value of L increases beyond 96 mm and decreases below 93 mm in length. Of course, for a practical application, parameter d must also be adjusted to obtain vertical E-field polarization of the straight circular-waveguide port. By following the optimization design approach for the mode converter, a dimension of 8.5 mm was arrived upon for parameter d.
Figure 4 shows the VSWR of the waveguide mode converter, with a value of less than 1.03:1 at 8.4 GHz. In addition, the polarization direction of the circular waveguide port is vertical. Figure 5 shows the fabricated waveguide mode converter, which was characterized by means of a commercial microwave vector network analyzer (VNA) and coaxial-to-waveguide adapters for connection to the VNA. Figure 6 shows that the measurement results are in good agreement with the performance predicted by the HFSS computer simulations.
In short, full-wave, finite-element analysis is an effective means for studying an N-port waveguide junction for waveguide mode conversion, and for developing a practical optimization method for designing a high-performance rectangular-to-circular waveguide mode converter. The optimization approach was validated by designing and fabricating a waveguide junction at 8.4 GHz with excellent return-loss performance, small size, and desired E-field polarization in the vertical direction. The prototype waveguide junction was characterized with a high-frequency commercial VNA system to evaluate forward and reflected transmission at and around its 8.4-GHz operating frequency. The performance measured for the prototype compare closely with the computer simulated performance numbers.
Acknowledgments
This article was supported by Major Program of National Natural Science Foundation of China (81090272).
References
1. J. Benford and J.A. Swegle, High-Power Microwaves, Artech House, Norwood, MA, 1992.
2. L.D. Bacon and L.F. Rinehart, "A brief technology survey of high-power microwave sources," Sandia Laboratories, Albuquerque, NM, technical report, 2001.
3. J.B. Robert and S. Edl, High-Power Microwave Sources and Technologies, IEEE, New York, 2001.
4. M. Gundersen, J. Dicken, and W. Nunnally, "Compact, portable pulsed power: physics and applications," 14th international pulsed power conference, Dallas TX, 2003.
5. S.T. Pai and Q. Zhang, Introduction to high power pulse technology, World Scientific Publishing Company, Ltd., Singapore, 1995.
6. H.E. Green, "The phase centre of a pure mode, smooth wall, conical horn," Progress In Electromagnetics Research B, Vol. 4, 2008, pp. 285-298.
7. R.C. Gupta and S.P. Singh, "Analysis of radiation patterns of compound box-horn antenna," Progress In Electromagnetics Research B, Vol. 76, 2007, pp. 31-44.
8. H.E. Green, "The radiation pattern of a conical horn," Journal of Electromagnetic Waves and Applications, Vol. 20, 2006, pp. 1149-1160.
9. Wes Lawson, Melany R. Arjona, Bart P. Hogan, and R.L. Ives, "The Design of Serpentine-Mode Converters for High-Power Microwave Applications," IEEE Transactions on Microwave Theory & Techniques, Vol. 48, No. 5, 2000, pp. 809-814.
10. W.A. Huting, J. W. Warren, and J.A. Krill, "Recent progress in circular high-power overmoded waveguide," The Johns Hopkins APL Technical Digest, 1991, 12, pp. 60-74
11. W.A. Huting, J. W. Warren, and J. A. Krill, "Some recent developments in circular overmoded waveguide," IEE Proceedings-H, Vol. 140, No. 6, December 1993.
12. A. Konrad, "Vector variational formulation of electromagnetic fields in anisotropic media," IEEE Transactions on Microwave Theory & Techniques, Vol. MTT-24, September 1976, pp. 553-559.
13. K. Ise, K. Inoue, and M. Koshiba, "Three-dimensional finite-element method with edgeelements for electromagnetic waveguide discontinuities," IEEE Transactions on Microwave Theory & Techniques, Vol. MTT-39, August 1991, pp. 1289-1295.
14. X. Zhou, "Physical spline finite element (PSFEM) solutions to one dimensional electromagnetic problems," Progress In Electromagnetics Research, Vol. 40, 271-294, 2003. 15. X. Zhou and G. Pan, "Application of physical spline FEM to waveguide problems," presented at PIERS 2000, Boston, MA, July 2002, in Progress In Electromagnetics Research Symposium, Proceedings, p. 77.