SLR Helps Shrink Quad-Band Filter
This file type includes high resolution graphics and schematics when applicable.
Bandpass filters (BPFs) are widely used in communications systems applications to transfer desired bands of signals, at the same time rejecting unwanted signals. As communications systems add more channels and bands, a growing number of BPFs is needed in these applications, or filters must be designed capable of channeling multiple bands. To demonstrate the feasibility of developing a quad-band BPF, a filter was designed based on stub-loaded resonators (SLRs) and modified from a three-band filter. A cross-coupling structure between the SLRs and the filter’s input/output ports was employed to enhance out-of-band performance, with passbands at 1.5, 2.5, 3.5, and 5.2 GHz. The computer simulations for the filter agree closely with the final measured results for a fabricated prototype.
Related Articles
• QAM Is Rising: 1024QAM And Beyond
• Differential Drive Optimizes Active Mixers
• MMIC PIN-Diode Limiters Operate to 20 GHz
Multiband bandpass filters are useful for wireless applications as a way to transfer a number of different channels with a smaller number of filters. A number of different design approaches have been employed, including the design of dual-band BPFs using stepped-impedance-resonator (SIR) architectures. By adjusting impedance ratio and electrical lengths of SIR, two desired operating frequencies can be obtained.1
In refs. 2 and 3, tri-band BPFs were designed based on SLRs. Most previous work on multiband BPF architectures focused on the design of dual-band and tri-band BPFs, with few methods exploring the design of quad-band BPFs.4-6 In ref. 4, coplanar-waveguide (CPW)-fed, dual-mode double-square-ring resonators were employed to obtain quad-band characteristics. In ref. 5, a quad-band BPF was achieved by combining four basic structures (outer-frame, U-shaped resonator, modified end-coupled microstrip line, and defected ground structures). In ref. 6, a quad-band BPF using a single type of half-wavelength resonator tapped by open-circuited stubs on a single layer was presented. However, the above-mentioned quad-band BPFs require multiple types of resonators or multilayered fabrication technology; these tend to increase filter size, cost, and complexity, in addition to limiting the application scope.
Based on a novel SLR, a compact BPF with quad-band characteristics was investigated. The quad-mode SLR can achieve four passbands simultaneously centered at 1.5, 2.5, 3.5, and 5.2 GHz. To improve the selectivity of the quad-band BPF, a cross-coupling structure between the SLRs and the filter’s input/output (I/O) ports is employed. Measurements performed on a fabricated prototype agree closely with simulated results from commercial computer simulation software.
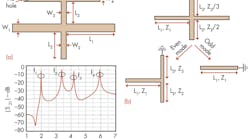
Figure 1(a) shows the structure of the novel quad-mode SLR, which consists of a common microstrip half-wavelength resonator, an open stub, and a T-type stub. One end of the T-type stub is grounded by means of a metallized via hole. The novel SLR is modified from a tri-mode SLR, as shown in Fig. 1(b). Due to its asymmetrical structure, it is difficult to obtain analytical resonant frequencies for the quad-mode SLR. But since the tri-mode SLR is symmetrical, an odd-even-mode method can be implemented, as shown in Fig. 1(b). Under conditions of Z1 = Z2 = Z3, the three resonant frequencies of the tri-mode SLR can be expressed by means of Eqs. 1-3:
fe1 = c/4[(L1 + L3](εe)0.5 (1)
fe2 = c/2[(L1 + L2](εe)0.5 (2)
fo1 = c/4L1(εe)0.5 (3)
where:
c = the speed of light in free space; and
εe = the effective dielectric constant of the substrate.
After substituting the shorted stub of tri-mode SLR with the T-type stub, quad-mode performance can be obtained. Figure 1(c) shows the simulated frequency responses of the novel quad-mode SLR under weakly capacitive coupling conditions. As can be seen, the quad-mode SLR obtains four resonant poles simultaneously.
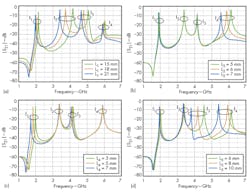
The transfer characteristics of the quad-mode SLR were studied for various dimensions with the help of the High-Frequency Structure Simulator (HFSS 11.0) full-wave electromagnetic (EM) simulation software from ANSYS, as shown in Fig. 2. It can be seen that the four resonant frequencies increase simultaneously as L1 decreases. But only one or two resonant frequencies increase as L2, L4, and L5 decrease, respectively. Therefore, by appropriately adjusting the resonator dimensions, four desired resonant frequencies can be achieved.
This file type includes high resolution graphics and schematics when applicable.
Sizing Up The Structure
This file type includes high resolution graphics and schematics when applicable.
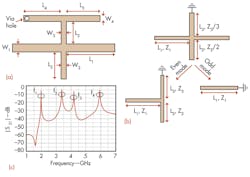
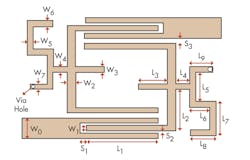
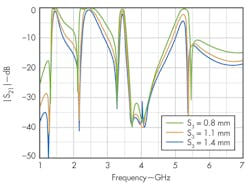
Figure 3 shows the structure of the novel quad-band BPF. It is composed of two SLRs and an interdigital I/O port. To realize good out-of-band performance, a cross-coupling structure between the SLRs and the I/O port was introduced, which can generate one transmission zero between two resonant frequencies.2 The filter was fabricated on RT/duroid 5880 circuit substrate material from Rogers Corp. with a thickness of 1.0 mm and a relative dielectric constant (εr) of 2.2. The dimensions were selected as follows: W0 =3.0 mm; W1 = W2 = W3 = W4 = W5 = W6 = W7 = 1.0 mm; L1 = 12.25 mm; L2 = 8.5 mm; L3 = 6.35 mm; L4 = 2.5 mm; L5 = 5.0 mm; L6 = 2.5 mm; L7 = 8.0 mm; L8 = 2.8 mm; L9 = 3.0 mm; S1 = 0.75 mm; S2 = 0.2 mm; and S3 = 0.35 mm. The via hole radius is 0.2 mm. As for bandwidth control, the external quality factor (Qe) and coupling coefficient (k) should be considered. The values of Qe and k are mainly determined by the gaps S3, as shown in Fig. 4.
The designed and fabricated quad-band BPF was measured with a model N5230A vector network analyzer (VNA) from Agilent Technologies, as shown in Fig. 5. The measured center frequencies and 3-dB fractional bandwidths (FBWs) of the quad-band filter are as follows: 1.5 GHz (FBW = 9.5%), 2.5 GHz (FBW = 19.3%), 3.5 GHz (FBW = 3.6%), and 5.2 GHz (FBW = 6.1%), as expected. The measured minimum passband insertion losses are 0.45, 0.22, 1.35, and 1.59 dB, respectively, while the return losses of each passband are better than 15 dB. In addition, the novel quad-band bandpass filter can generate transmission zeros with a better than 20-dB suppression degree on both sides of the passbands, giving much improved selectivity.
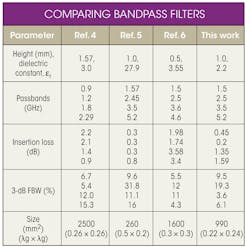
The overall size of this quad-band filter is about 30 × 33 mm, as shown in Fig. 6. A comparison of this novel quad-band BPF with other reported quad-band BPFs is shown in the table, which depicts that the proposed BPF has good characteristics with compact size. Due to its simple structure, compact size, and good performance, the novel BPF presented here should be quite suitable for multiband communications systems.
Acknowledgment
This work was supported by the National Natural Science Foundation of China (NFSC) under Grant No. 61301071 and China Scholarship Council.
Lei Chen, Lecturer
School of Electronic and Information Engineering,
Xi’an Technological University, Xi’an, People’s Republic of China, 710032
Feng Wei
Associate Professor
National Key Laboratory of Antennas and Microwave Technology,
Xidian University, Xi’an, People’s Republic of China, 710071
This file type includes high resolution graphics and schematics when applicable.
References
This file type includes high resolution graphics and schematics when applicable.
1. J.-T. Kuo, T.-H. Yeh, and C.-C. Yeh, “Design of microstrip bandpass filters with a dual-passband response,” IEEE Transactions on Microwave Theory & Techniques, Vol. 53, No. 4, 2005, pp. 1331-1337.
Related Articles
• QAM Is Rising: 1024QAM And Beyond
• Differential Drive Optimizes Active Mixers
• MMIC PIN-Diode Limiters Operate to 20 GHz
2. F.C. Chen, Q.X. Chu, and Z.H. Tu, “Tri-band bandpass filter using stub loaded resonators,” Electronics Letters, Vol.44, No.12, pp.747-749, 2008.
3. X.-Y. Zhang, Q. Xue, and B.-J. Hu, “Planar tri-band bandpass filter with compact size,” IEEE Microwave & Wireless Component Letters, Vol. 20, No. 5, 2010, pp. 262-264.
4. J.-C. Liu, J.-W. Wang, B.-H. Zeng, and D.-C. Chang, “CPW-fed dual-mode double-square-ring resonators for quad-band filters,” IEEE Microwave & Wireless Component Letters, Vol. 20, No. 3, 2010, pp. 142–144.
5. C.-M. Cheng and C.-F. Yang, “Develop quad-band (1.57/2.45/ 3.5/5.2 GHz) bandpass filters on ceramic substrate,” IEEE Microwave & Wireless Component Letters, Vol. 20, No. 5, 2010, pp. 268-270.
6. J.Y. Wu and W.H. Tu, “Design of quad-band bandpass filter with multiple transmission zeros,” Electronics Letters, Vol. 47, No. 8, 2011, pp. 502-503.
This file type includes high resolution graphics and schematics when applicable.