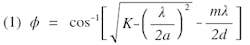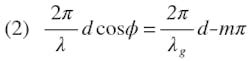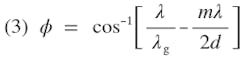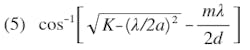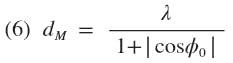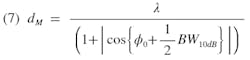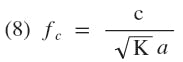Beam Pointing Direction of Traveling-Wave Arrays
June, 1969
Dielectric-filled waveguide, traveling-wave arrays can be designed for main beams pointing between broadside and forward endfire or between broadside and rear endfire. This beam pointing direction is a function of frequency, the waveguide width, the spacing and phasing of the radiating elements, and the dielectric constant of the material used in the array.
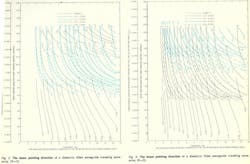
The curves in Figs. 1-11 relate these parameters. A waveguide filled with dielectric material reduces the waveguide wavelength and thereby reduces the size of the waveguide. The use of dielectric-loaded waveguide therefore provides not only a flexibility of design through several design options, but reduced fabrication costs as well.
Each curve represents a different dielectric constant, of integer value (K = 1 through 9). Graphs have been included for fused silica and Pyroceram brand glass-ceramic with dielectric constants of 3.78 and 5.55 respectively. These two ceramics have been found to be especially suited for waveguide loading applications, having a negligible dielectric constant variation over extended temperature ranges. For other specifically desired dielectric constants, parameters can be obtained by interpolation from the available graphs.
The curves show the maximum normalized interelement spacing without gain reducing grating lobes or secondary main beams appearing. Given specifications such as beam position and frequency, the antenna designer can immediately obtain parameters from the graphs provided.
The curves are intended to present all the possibilities and trade-offs available in evaluating a traveling-wave array rather than a specific design procedure.
This file type includes high resolution graphics and schematics when applicapable.
Use of curves and their relation to parameters
The dependence of the main beam pointing direction on the various parameters of a dielectric-filled waveguide array may be described as follows:
where
ϕ = the main beam pointing direction from forward endfire
K = dielectric constant of the material investigated
λ = free space wavelength
α = inside width of the rectangular waveguide
m = 1 or 3 when slots are staggered
m = 0 to 2 when slots are collinear (in line)
d = spacing between adjacent elements (slots) as measured along the waveguide axis.
Figures 1 through 11 are graphical representations of Equation 1. If forward endfire is the direction of the waveguide propagation and rear endfire is the direction of the source or feed with respect to the radiating elements (Fig. A), then the angle of the main beam pointing direction from forward endfire is the ordinate of the curves. The other ordinate is the maximum normalized interelement spacing not allowing grating lobes or secondary main beams to appear. All parameters defined in Equation 1 are presented on Figs. 1 through 11. When m is equal to zero, the beam position is independent of the interelement spacing; therefore, the dotted line representing this case is applicable to all interelement spacings that do not allow grating lobes to appear in the radiation pattern.
Antennas filled with certain types of these dielectric materials can generate either of two beams (corresponding to m equals 0 or 2 for collinear slots or to m equals 1 or 3 for staggered slots). Ambiguities do not exist since the two beams appear over non-overlapping bandwidths.
Example problem considering various dielectrics
A beam position of 60 degrees from forward endfire at a frequency of 5 GHz is desired. An interelement spacing close to 0.65λ will be investigated. Table 1 gives the possible parameters for this problem. As can be seen, many trade-offs exist. The waveguide width and frequency sensitivity vary depending on the dielectric material available. Generally, the beam position is less sensitive to waveguide tolerances for wider widths. The solution to this problem is thus dependent on the maximum waveguide width allowable, the tolerable beam shift due to the required frequency bandwidth, and the dielectric materials that are obtainable.
Example problem showing interpolation technqiues
It is required to design an array with a beam pointing 70 degrees from forward endfire at 10 GHz. If other considerations dictate usage of a material whose dielectric constant is 2.5, which is not covered by any of the curves of Figs. 1 through 11, a design could be obtained by interpolating between the curves representing the two integer dielectric constants closest to 2.5. The results in Table 2 follow from an interpolation of the curves in Figs. 2 and 3.
The second design is chosen because it is less frequency sensitive even though it is wider.
Example problem using a specific dielectric material
An antenna is assumed to be mounted on a missile parallel to the missile axis; the antenna is to be fed from the forward missile end. A beam angle of 50 degrees from the forward missile axis at a frequency of 6 GHz is desired. (ϕ = 180-50 deg.) Due to the insensitivity of the dielectric constant of Pyroceram brand glass-ceramic to temperature, it is chosen as the loading material. Table 3 presents the solution to this problem. The second design is chosen because it is less frequency sensitive.
This file type includes high resolution graphics and schematics when applicapable.
Appendix
This file type includes high resolution graphics and schematics when applicapable.
A. Derivation of the main beam-pointing equation
A linear traveling-wave array of radiating elements with a constant interelement spacing, d, is considered; see Fig. A. The change in phase from a to c is 2π/λ ∙ d cos ϕ where λ is the free space wavelength and ϕ the main beam pointing direction from forward endfire. Similarly, the phase change from a to b is 2π/λg ∙ d; λg is the waveguide wavelength. An additional phase shift of –mπ (m = 0, 1, 2, 3) is introduced with each succeeding element. The value of m depends on how the elements are fed—in or out of phase (m = 1 and m = 3 correspond to staggered slots and m = 0 and m = 2 correspond to collinear or inline slots). Points c and b are in phase yielding.
Solving Eq. 2 for ϕ gives an expression for the main beam pointing direction
For the TE10 mode of the waveguide wavelength, λg, is related to the relative dielectric constant, K, and the inside width, a, of the rectangular waveguide by
The beam pointing direction is, thus
Eq. 5 represents the beam pointing direction for the array factor of an array of omnidirectional elements.
B. Bias toward broadside
The effective bias toward broadside of the beam pointing direction of traveling-wave arrays is caused by the variation of the magnitude of the element factor from broadside to endfire. Radiation pattern beams of non-broadside arrays are asymmetrical because the magnitude of the element factor is maximum at broadside and decreases toward forward endfire and rear endfire. In particular, the forward endfire (rear endfire) portion of the main lobe of a non-broadside beam is somewhat lower than the corresponding portion of a broadside beam from an array of the same length. Lowering the portion of the main beam closest to forward endfire (rear endfire) with respect to the portion closest to broadside effectively moves the beam peak toward broadside. The wider the beam and the closer it is to forward endfire (rear endfire), the greater the relative reduction of the forward endfire (rear endfire) portion of the main beam and the greater the effective bias toward broadside.
C. Grating lobes
The maximum interelement spacing, dM, of radiating elements in a traveling-wave array (which will not allow gain reducing grating lobes to appear in the radiation pattern) is a function of the angular offset, ϕ0, of the main beam from endfire, as expressed in Eq. 6 for infinitely narrow beamwidths.
where λ is the operating wavelength. A more general expression applicable to arrays of various beamwidths is
where BW10 dB is the 10 dB beamwidth or the angular width of the main beam measured at the 10 dB down points. Figs. 1 through 11 are each plotted with interelement spacings of 0.55λ and 0.65λ which correspond to minimum angular offsets of the main beam from endfire of 34.9 degrees and 57.3 degrees, respectively, (which will not allow grating lobes to appear in the radiation pattern) for infinitely narrow beams. The appropriate portions of the curves have been eliminated due to grating lobes appearing in the radiation pattern as predicted by Eq. 6. The antenna designer should use the more general expression of Eq. 7 to check their particular array for possible grating lobes.
D. Double moding
Eq. 5 was derived for a TE10 mode of propagation in a rectangular waveguide. Under certain conditions the TE20 mode will propagate, and those conditions (waveguide widths allowing TE20 cut off frequencies below the operating frequency) have been eliminated from the curves. The expression for TE20 cut off frequency is
where
c = velocity of light
K = dielectric constant
a = inside width of the rectangular waveguide
E. Broadside beam designs
Traveling-wave arrays are not usually designed with broadside beams. Commonly used longitudinal shunt slot radiating elements staggered (non-staggered) about the waveguide broadwall centerline are spaced odd (even) multiples of a half waveguide wavelength apart along the traveling-wave array when broadside beams are desired. However, the input admittance of the array for either odd or even multiples of half waveguide wavelength interelement spacing is the sum of the admittances of the individual shunt slot radiating elements plus the characteristic admittance of the waveguide. Since the sum of the admittances of the individual shunt elements cannot equal zero, the input admittance of the array cannot equal the characteristic admittance of the waveguide; thus, the array will not be matched without a transformer. Therefore, the more efficient standing wave arrays rather than traveling-wave arrays are commonly used to generate broadside beams.
The basic design curves, Figs. 1 through 11, include the broadside beam pointing direction. However, the engineer should not design a traveling-wave array with a beam pointing direction closer than 5 degrees from a broadside at all operating frequencies because of the matching problems.
Figures
This file type includes high resolution graphics and schematics when applicapable.