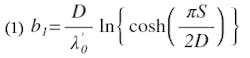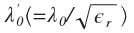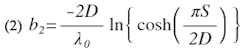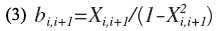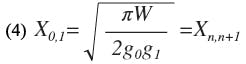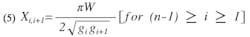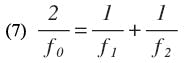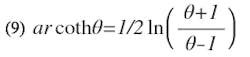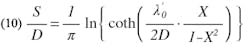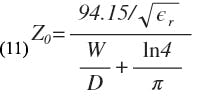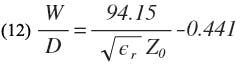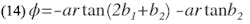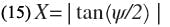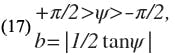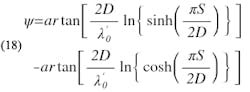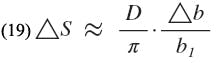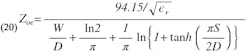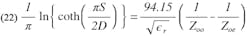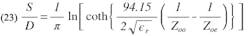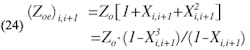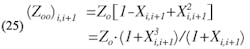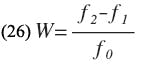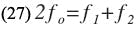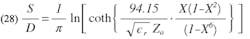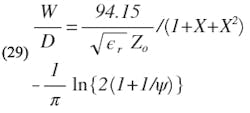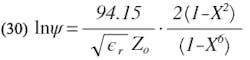June, 1968
Download this article in .PDF format
In designing these filters, first decide upon the required frequency response and the rate of attenuation beyond cut-off; then calculate the number of resonators required and the values of the equivalent low-pass prototype elements.Design procedure
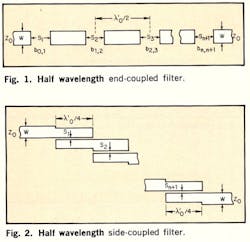
For the end-coupled filter, Fig. 1, it is necessary to determine the susceptance of the capacitative gaps between resonant elements; 1. as a function of strip-line geometry and permittivity of the dielectric between ground planes, and 2. as a function of the required frequency response and normalized bandwidth. Next, by eliminating the susceptance values from the two sets of equations, it is possible to obtain expressions which explicitly relate the rations S/D and W/D (See Figs. 1-3) in terms of bandwidth and frequency response. The spacings between strips will differ from one resonator to another, being least for the first and last sections.
For the side-coupled filter, Fig. 2, a similar procedure is adopted, except that instead of susceptances it is necessary to evaluate even- and odd-mode characteristic impedance of the coupled resonator strips. By eliminating the impedance values from two further sets of equations, the ratios S/D and W/D are obtained as a function of bandwidth and frequency response. As with end-coupled filters, the spacings between resonator strips will be smallest for the end sections, but the strip widths differ from one section to another. However, for bandwidths less than 1%, the value of W/D does not significantly differ from that obtained for the terminal strips.
A difference exists between the electrical length of the resonator strips, λʹ0/2, and the physical length for both filter types. Due to fringe fields, the electrical length is greater than the physical one, and a reduction in the latter is essential if the filter is to have an accurately positioned center frequency. Unfortunately, the formulas available to determine the necessary reduction in physical length are only approximate and have not been given in this article.
Design formulas for end-coupled filters
and
Equations (1) and (2) are accurate for W/D > 1.2. For S/D < 0.2, | b1 | > 10 | b2 |, and for S/D < 0.1, | b1 | > 75 | b2 |. For the preliminary analysis of the end-coupled filter, S/D is assumed small enough that | b2 | may be neglected.
The normalized susceptance of the (i + 1)-th gap of an end-coupled filter with n stages, bi,j+1, may be expressed as follows:
where
and
where
f1 and f2 are the lower and upper cut-off frequencies, respectively, and
where f0 is the center frequency of the filter and g is the normalized value of a low-pass prototype element.
Equation 1 can be rearranged into a form in which S/D is expressed as an explicit function of the series susceptance, b1. From (1),
and utilizing the identity
substituting for b1 from Eq. 3, and omitting the i subscripts, Eq. 8 becomes
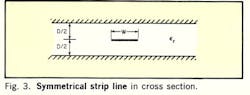
The value of W/D can be found from the equation given by Cohn for the characteristic impedance, Zo, of a symmetrical strip line (Fig. 3):
from which it follows:
Design formulas for end-coupled filters (continued)
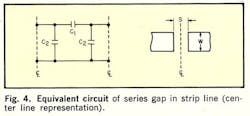
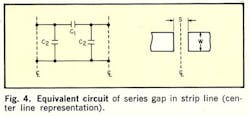
The following analysis, which accounts for b1 and b2, shows that Eq. 10 may be used for S/D as large as 0.6 accuracy of better than 1% providing λʹ0/D ≥ 6.Referring to the equivalent circuit of the series gap (Fig. 4), parameter X may be expressed as a function of both b1 and b2:
where
Therefore,
where
From Eq. 3, b = X/(1-X2).
Substituting from Eq. 15 and providing
Substituting for b1 and b2 from Eqs. 1 and 2 into Eq. 16, and simplifying, ψ may be expressed directly in terms of S/D:
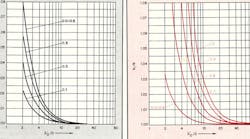
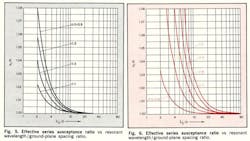
Utilizing equations 17 and 18, b can be obtained as a function of S/D and λʹ0/D and compared with b1 obtained from Eq. 1 as a function of the same parameters. Graphs have been prepared with the ratios b/b1 and b1/b plotted in Figs. 5 and 6 as functions of λʹ0/D for 1.0 ≥ S/D ≥ 0.1. Note that for S/D < 0.5, b > b1 and for S/D > 0.6, b1 < b.
The effect of the difference between b and b1 on the value of strip spacing can be determined for relatively small differences by differentiating S with respect to b1 in Eq. 10. Upon simplification, the following result is obtained:
where â b = b ~ b1. For b1 λʹ0/D ≤ 0.5, Eq. 19 has a maximum error of approximately 4%. By considering Figs. 5 and 6, in conjunction with Eq. 19, the error in gap spacing obtained by using Eq. 10 (which does not account for the shunt susceptances, b2) may be determined.
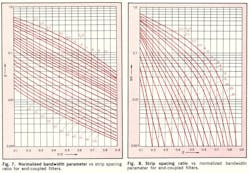
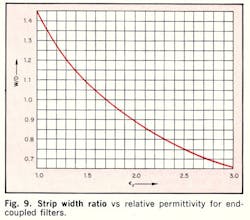
Unfortunately, it is not possible to obtain an explicit expression for S/D in terms of X, accounting for b1 and b2, because of the transcendental nature of Eq. 18. Nevertheless, utilizing Eqs. 12, 15 and 18, a set of graphs has been prepared giving X as a function of S/D for 100 ≥ λʹ0/D ≥ 2 and 1 > X > 0 (Figs. 7 and 8) and W/D as a function of ϵr for Zo = 50 Ω (Fig. 9).
Design formulas for side-coupled filters
The equations which related the even and odd mode impedance, Zoe and Zoo, respectively, to W/D, S/D and ϵr have been given by Cohn (Ref. 4) and may be expressed as follows:Design formulas for side-coupled filters
and
Equations 20 and 21 are accurate to approximately 1% for W/D = 0.35, and become increasingly accurate for W/D > 0.35, and become increasingly accurate for W/D > 0.35.
Rearranging (20) and (21), and subtracting from the other, the ratio W/D can be eliminated and the following expression obtained:
Solving for S/D using a similar procedure to that used to obtain Eq. 10 from Eq. 1, S/D can be expressed explicitly as a function of ϵr, Zoo and Zoe:
A further set of equations relating Zoe and Zoo to the bandwidth parameter, X, have also been given by Cohn (Ref. 2), and may be expressed as follows:
and
where n > i > 0 X is defined in Eqs. 4 and 5 with
Substituting for Zoe and Zoo from Eqs. 24 and 25 into Eq. 23, and eliminating the i subscripts and simplifying,
As the maximum permissible value of X is 0.5 (Ref. 3), the term X6 can usually be neglected.
Substituting for S/D from Eq. 28 into Eq. 20, and for Zoe from Eq. 24, an explicit expression for W/D is obtained:
where
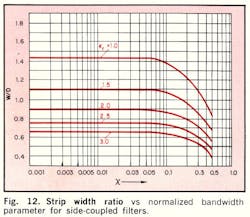
For very narrow bandwidths, corresponding to X < 0.01, W/D can be taken as equal to that of the terminating strips, as given by Eq. 15 or graphically in Fig. 9. Moreover, both the X2 and X6 terms can be neglected in Eq. 28 for narrow bandwidths.
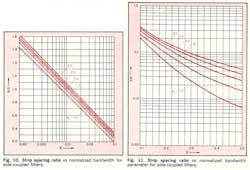
Hence, ratios S/D and W/D can be found for side-coupled filters as a function of the parameters X, ϵr, and Zo. Additional graphs have been prepared (Figs. 10-12) in which S/D and W/D are plotted as functions of X for values of ϵr and for Zo = 50Ω.
- E.G. Bradley, “Design and Development of Strip Line Filters,” IRE Trans. MTT, (April, 1956).
- S.B. Cohn, “Parallel Coupled Strip Line Resonator Filters,” L’Onde [France], (October, 1957).
- J.K. Richardson, “Gap Spacing for End Coupled and Side Coupled Band Bass Filters,” IEEE Trans. MTT. (June, 1967).
- S.B. Cohn, “Shielded Coupled Strip Transmission Line,” IRE Trans. MTT, (October, 1957).
- E.G. Bradley, op.cit.
- S.B. Cohn, “Direct Coupled Resonator Filters,” Proc. IRE, (February, 1957).
- H.M. Altschuler and A.A. Oliner, “Discontinuities in the Centre Conductor of Symmetric Strip Transmission Line,” IRE Trans. MTT, (May, 1960).
- G.L. Matthew, L. Young and E.M.I. Jones, Microwave Filters, Impedance-Matching Networks, and Coupling Structures, (McGraw-Hill Book Co., 1964).
- E. Rubins, W. Fromm and H. Keen, “New Techniques for High Q Microwave Components,” IRE Convention Record, Part 8, (1954).