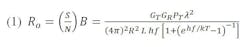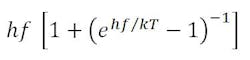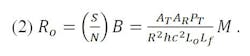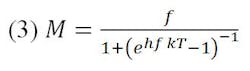Lasers vs. Microwaves for Deep-Space Communications
This file type includes high resolution graphics and schematics when applicapable.
May, 1967
The advent of lasers raises the possibility of extending coherent techniques into the optical region, particularly for deep-space communications. This article compares microwave and laser links for spacecraft-to-earth communications. Fundamental and practical limitations are discussed.
The performance of a telecommunication link can be measured by such criteria as amount of data, trustworthiness, and economy in transmission of data. In this analysis, primary emphasis is placed on increasing the amount of data while maintaining its quality. Economy of data transmission remains important but secondary; realistic cost evaluations must be related to specific candidate systems as they develop from basic systems studies and research.
The product of transmitted data quality and quantity (the information rate parameter Ro) is then taken as a performance criterion, and the one-way transmission equation is written in terms of this product:
Here the signal-to-noise ratio, S/N, represents signal quality; the bandwidth, B, represents quantity; the expression
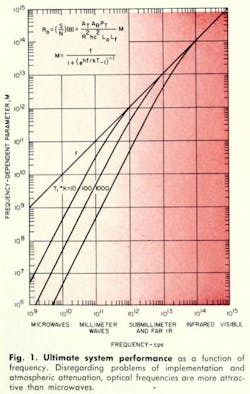
represents the ideal noise limit where T is the temperature at an ideal receiver input. In the microwave region, where kT ≫ hf, this expression converges to the familiar quantity kT; in the optical region, where kT ≪ hf, to hf. Insertion of the functional frequency dependencies of the transmitter and receiver antenna gain (G = 4π A / λ2 ) in Eq. 1 gives:
Lo represents the fixed system losses and Lf the frequency-dependent losses (greater than unity). M may be considered a measure of potential performance in the absence of practical restrictions and is given by
Eqs. 2 and 3 document the explicit functional frequency dependencies and separate them from the physical parameters of the transmission link equation. However, in practical systems, some of these physical parameters indirectly depend on frequency. Consider for example, the frequency dependence placed on a spaceborne transmitting antenna by achievable pointing accuracy. Such a limit sets a minimum allowable bandwidth (or maximum gain), thereby requiring that the effective diameter of the transmitting antenna decrease inversely with frequency. This and other such restrictions must be included when applying the transmission equation to select an optimum frequency.
The explicit functional frequency given by M is discussed next as are the implicit frequency dependences due to various practical limitations imposed on the transmitting antenna area, AT; receiving antenna area, AR; transmitted power, PT; and losses in atmospheric transmission Lf.
Functional frequency dependence
This file type includes high resolution graphics and schematics when applicapable.
Transmitting antenna area
The effective area of a spacecraft transmitting antenna is limited by one of three practical considerations:
- Weight and size limitations imposed by the vehicle,
- Antenna fabrication tolerances, and
- Transmitting beamwidth demanded by the limitation of pointing accuracy.
Although there is some interrelation among these factors (for example, an extensible antenna may be used for increased diameter at the expense of dimensional tolerances), one generally will dominate within a certain frequency range.
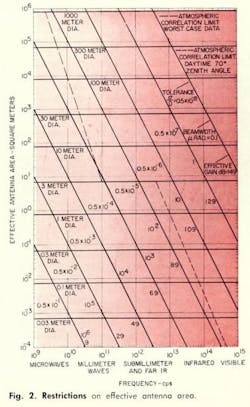
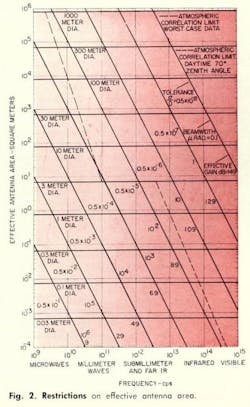
Similarly, a given pointing accuracy requires a certain beamwidth and hence represents a gain limit. Thus, the same family curves can represent the restriction on the transmitting antenna area caused by either fabrication tolerance or pointing accuracy limitations. The curves, evaluated for an approximate 3-dB loss, result in lines of constant negative slope on the log-log plot of Fig. 2 and are labeled in terms of σ/D, beamwidth, and effective gain (3-dB loss from an ideal included).
From Fig. 2 the systems engineer can determine the frequency dependence of transmitting antenna area appropriate from assumptions of vehicle constraints, practical fabrication tolerances, and achievable pointing accuracy.
Receiving antenna area
This file type includes high resolution graphics and schematics when applicapable.
The same kinds of restrictions apply to receiving antenna area as to the transmitting antenna. The useful area of a single element may be limited by allowable size, achievable tolerances, or (for coherent reception) achievable pointing accuracy. For a satellite receiving station, limiting values may not differ too much from those for a deep space vehicle. On the other hand, for a ground station, over-all aperture diameter will generally not be restricted by installation requirements; but a single aperture element will be subject to limitations from atmospheric phase distortion of the signal wavefront over the aperture.
Little quantitative information is available on such atmospheric anomalies as wavefront corrugation, tilt, or unequal illumination of the aperture. However, the nature of the restriction is suggested by available data from the NBS experiment at Maui, Hawaii (1956). The assumption is made that the wavefront distortions, corresponding to the phase deviations experimentally measured as a function of baseline, have an effect similar to dimensional deviations of the antenna surface caused by fabrication tolerances.
In the optical region of the spectrum, atmospheric phase correlation length limits the effective aperture diameter for coherent detection. This correlation length is assumed to vary as λ and typical values have been given for various environmental conditions. The aperture area corresponding to a 3-dB signal decorrelation loss for typical daytime atmospheric turbulence is plotted in Fig. 2 for a 70-deg zenith angle. This restriction applies only to coherent reception.
Amplitude fluctuations are also present in the received wavefront as a result of atmospheric disturbances. These may require physical apertures considerably larger than the effective aperture limit to average reception over several amplitude correlation lengths. In the visible region, for example, where the effective aperture diameter for coherent detection is only a few cm, the amplitude correlation length is typically 10 cm and a 30 cm aperture is required to reduce rms deviations in received signal power to about 10 percent.
Transmitted power
Frequency-dependent restrictions on transmitter power are related to the method of power generation. At microwave and mm-wave frequencies, traveling-wave tubes are most satisfactory in providing high power. In general, however, the maximum power capability of TWT amplifiers is inversely proportional to frequency.
At optical frequencies, lasers represent the only power source having the spatial coherence necessary for high-gain (essentially diffraction-limited) apertures as well as the temporal coherence to permit the advantages of coherent detection. The principal limitation on power generated is heat dissipation in the laser cavity due to low conversion efficiencies. There is no significant systematic dependence on frequency, performance being related to the different specific laser mechanisms.
In either portion of the spectrum, an increase in power can always be achieved by paralleling units, although in the optical region phase-locking the various elements will be more difficult. Hence, the effective power limitation is set by weight, size, and power supply restrictions.
Atmospheric losses
Transmission losses occur in the atmosphere by absorption of electromagnetic radiation by the constituent gases (especially water vapor), and in the optical region, because of aerosol and molecular scattering. Absorption occurs in bands rather than as a systematic variation and becomes significant at frequencies higher than 10 Gc. Transmission “Windows” between the bands exist in the millimeter-wave region, but transmission at submillimeter waves is believed to be generally blocked.
Windows appear again in the infrared, while in the visible region absorption occurs only in well-separated lines. Scattering at low altitudes from aerosols generally accounts for the predominant loss in the visible region, with the transmission decreasing for shorter wavelengths.
Rain and fog begin to seriously affect transmission in the millimeter-wave region, with the fog losses increasing prohibitively at optical frequencies. Thus, an optical communication link would be effectively blacked out by cloud cover.
System noise
This file type includes high resolution graphics and schematics when applicapable.
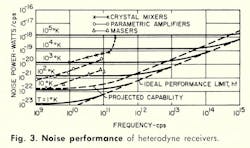
Essentially, system noise has no explicit frequency dependence other than that already included in the parameter M. It depends in practice, however, on external noise sources, on achievable receiver noise temperatures in the RF region and on detector quantum and heterodyne efficiencies in the optical region.
Fixed losses
In addition to frequency and weather-dependent transmission losses and detection losses accounted for by the effective value taken for M, there are several practical losses which apply generally to all systems. Limitations on effective transmitting and receiving apertures have been given for conditions to which a 3-dB decrease in effective gain from the ideal is expected. Thus, a 6-dB loss must be allocated to these components. A further 1 dB is taken to cover miscellaneous transmission losses in the equipment, so that a total of 7 dB is assumed for fixed system losses.
System performance
- No atmospheric losses (corresponding to a satellite receiving station),
- Atmospheric losses due to clear weather conditions and
- Atmospheric losses due to poor weather conditions.
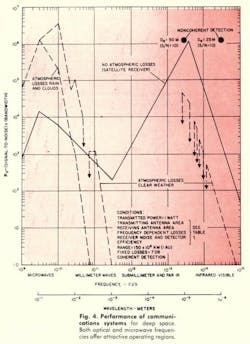
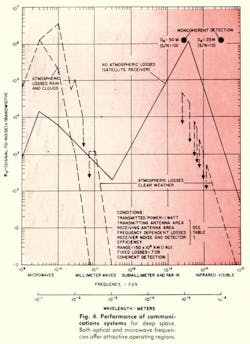
The product (S/N)B, or information-rate parameter R0, is plotted in Fig. 4 for the three cases considered. The sharp peaks and valleys result from the discontinuous nature of the parametric restrictions selected. Undue significance should not be attached to their exact positions, which depend on the particular values given in Table 1 as representative of practical limits.
It should also be noted that the curves in the optical region represent performance limitations on coherent detection. For noncoherent detection, pointing accuracy and atmospheric distortions do not impose restrictions on receiver aperture area. In general, the performance will vary inversely with frequency in the optical region (for no atmosphere or for clear weather) rather than as the inverse cube. On the other hand, receiver noise levels may be very much higher. A comparison is made between coherent and noncoherent performance at two specific wavelengths as in Fig. 4.
Satellite receiver
This file type includes high resolution graphics and schematics when applicapable.
Ground-based receiver
Similar maxima are indicated for a ground-based receiver for clear weather. Performance at microwave frequencies, however, is increasing to about 10 Gc, where atmospheric distortions tend to limit aperture size. This assumes the possibility of a single-element receiving antenna with an effective diameter of 100 meters and a fabrication tolerance of about σ/D = 2 x 10-5 or, alternatively, the employment of an equivalent antenna array. Where information rates of 106 bits per sec are considered, an array large enough to provide this effective aperture at low elevation angles will require compensation for variation not only of the carrier phase but also of the signal delay across the aperture.
The performance peak in the infrared is lowered and shifted slightly to longer wavelengths by atmospheric distortion; transmission in the submillimeter and far infrared region is effectively cancelled by atmospheric absorption. Smaller subsidiary peaks appear, however, at the 35- and 94-Gc “windows.”
The expected performance of two noncoherent optical systems is included. Because the detection mechanisms for these systems vary, it is not convenient to show a general functional dependence of performance on frequency.
When the restrictions imposed by clouds and rain are considered, the familiar single-performance maximum appears in the microwave region at about 3 Gc. Undue significance should not be given to the exact position of the peak as shown, since it is determined more by the somewhat arbitrary limits chosen for the transmitter and receiver antenna dimensions than by the more fundamental restrictions of antenna noise temperature and atmospheric transmission.
System configurations
The curves of Fig. 4 indicate the relative performance of deep-space communication links operating in the various regions of the frequency spectrum. It is evident that a major hindrance to the improvement promised at higher frequencies is presented by the attenuation and distortion of the atmosphere.
Space missions likely to require the wide signal bandwidths are those involving real-time transmission of data and hence an essentially continuous capability. (Such a requirement can be expected for a fly-by mission, a landing mission, or a mission requiring voice communication.) At microwave frequencies, continuous coverage can be achieved under all weather conditions, and a direct spacecraft-to-earth link is appropriate. However, at optical frequencies, clouds may completely disable a ground site. Thus, if a continuous link is to be established between a spacecraft and earth within an acceptable atmospheric loss, alternative transmission configurations must be considered for wavelengths shorter than microwave.
There seems little reason to consider seriously a millimeter-wave system except possibly for a space vehicle-to-satellite link if a breakthrough in receiver technology should occur. For a ground receiver, performance at 30 Gc comparable to that at 3 Gc would require an equivalent antenna area with means to correlate atmospheric phase distortions over the aperture, or an order of magnitude increase in other system parameters. At 94 Gc, ground receiver performance is down by another two orders of magnitude from 30 Gc.
Potential microwave and optical systems are discussed briefly below and appropriate parameters are then given for the most promising cases.
Direct microwave link
This file type includes high resolution graphics and schematics when applicapable.
Direct microwave link
Near 3 Gc, atmospheric losses and restrictions on potential performance are small. At the same time, much larger apertures can reasonably be contemplated for ground-based than for satellite-borne receivers. Thus, a direct spacecraft-to-earth link is the obvious choice for a microwave system.
Suitable components for such a system have been under progressive development and only modest advancement in the state of the art should be required to permit information rates on the order of 106 bits per sec. Note that for the extrapolated antenna gains considered, a 10-W space vehicle transmitter would be sufficient. Indeed, the penalty paid for a microwave system is in the size of transmitting and receiving antennas needed to achieve the desired performance at moderate transmitted-power levels.
Direct optical link
To provide an essentially continuous direct optical link between a spacecraft and earth, multiple ground stations evidently would be necessary (i.e., several times the number needed to provide the requisite angular coverage). The number of additional stations required will depend on the statistical weather conditions at the specific sites available. The availability of enough good sites could, in principle, result in an over-all cost saving because of the smaller installation cost of an optical receiver.
Coherent 10-μ system. For coherent reception, the CO2 laser wavelength at 10.6 μ lies very near the performance peak of Fig. 4. Coupled with the high efficiency of the CO2 laser, this wavelength is an obvious choice for a coherent optical system. It is evident at this wavelength that multi-element apertures may be required in very high data rate systems. However, at 10.6 μ the (S/N)B product for each element is more than sufficient to phase-lock the local oscillator to follow the low-frequency signal-phase distortions imparted by the atmosphere. The elementary signals then can be correlated at the heterodyne difference frequency to provide a useful signal-to-noise ratio at the information bandwidth.
A total effective aperture diameter of about 2 meters, consisting of say 33 elements, would equal the performance of the 3-Gc system considered (100-meter receiving antenna diameter). The number of elements could be reduced somewhat by using larger, but less efficient, elemental apertures. However, implementation of such a system would not be trivial and substantial increases in other parameter values would need to be considered for high data-rate links.
Noncoherent 10.6-μ system. Noncoherent detection of 10.6 μ is thermal-noise limited. The sensitivity of the detector in this mode is about three orders of magnitude less than in the coherent mode. (Because the limiting noise is independent of the signal, the actual degradation factor depends on the square root of the signal-to-noise ratio, which is taken here to be 10.) In as much as atmospheric phase correlation lengths, do not restrict the elemental aperture area, a single large “photon bucket” may be used. But practical fabrication tolerances and detector dimensions will set an upper limit on noncoherent aperture diameters.
If a σ/D ratio comparable to that postulated for the 100-meter microwave antenna could be achieved for an optical reflector, diameters as large as 50 meters, sufficient to match the performance of the microwave link, might be feasible. (Because the limiting noise level is determined to a large extent by stray capacitance at the detector output, division of the aperture into elements with separate detectors could degrade performance severely.) In spite of the reduced complexity, the much greater aperture area required for noncoherent as opposed to coherent reception at 10. 6 μ makes this system unattractive.
Noncoherent 0.5-μ system. The communication link performance indicated in Fig. 4 discourages wide-band coherent detection in the visible region of the spectrum for a ground-based system in view of the short-phase correlation distances.
However, the situation is somewhat improved for noncoherent detection. For a system operating at approximately 0.5 μ a photomultiplier detector can provide essentially noise-free quantum detection. As compared with coherent detection at 10.6 μ, detection sensitivity will be down by a factor of two due to the higher quantum noise limit for noncoherent detection; another factor of about 2.5 is needed to account for the lower quantum efficiency of the photoemissive detector surface; a further loss factor of 20 is due to the increase in quantum noise level with frequency.
Sky background illumination will cause additional degradation depending on receiver field of view and aperture size. For an optimized system this might be as low as 3 dB. The total sensitivity indicated is about two orders of magnitude worse than that of a coherent 10.6-μ receiver but an order of magnitude better than a noncoherent 10.6-μ system.
However, a 0.5-μ system suffers from a major disadvantage: present lasers in this region of the spectrum are only 0.1 percent efficient. Barring discovery of a new laser material, over-all system performance would be over an order of magnitude below the low level anticipated for a noncoherent CO2 (10.6-μ) system. While direct solar pumping of the laser might give a small improvement in over-all efficiency, the improvement would not overcome the basic deficiency of the laser.
Higher laser efficiencies are available in the near and intermediate infrared at 0.84 and 2.1 μ. But over-all system performance at these wavelengths is currently lower than at 0.5 percent when refrigeration requirements and poorer detection sensitivities are taken into account.
Satellite optical link
This file type includes high resolution graphics and schematics when applicapable.
Another way to exploit the increased aperture gains at optical wavelengths, while avoiding blackout caused by poor weather conditions, is to use a satellite relay station. The spacecraft-to-satellite link would take advantage of the higher aperture gains available at optical wavelengths while a microwave relay link to earth would circumvent atmospheric losses. Except for a few limited geometries, a single synchronous satellite could provide a continuous link with the spacecraft so that a single satellite receiver and ground station might suffice for the full system.
The cost of a satellite receiver must therefore be weighed against the cost (including maintenance) of three or four large-aperture ground-based microwave receivers, or of a greater number of relatively small-aperture, ground-based optical receivers.
Because of the CO2 laser’s much higher over-all efficiency, 10.6 μ is the only wavelength worth serious consideration at this time for an optical spacecraft-to-satellite link. Fig. 4 shows that performance of a coherent system with one-meter transmitting and receiving apertures is slightly poorer than that of the 3-Gc spacecraft-to-earth microwave link. If effective transmitting and receiving aperture diameters are increased from 1 to 1.2 meters (still within the pointing error limitation assumed), comparable performance is obtained. Except by increased transmitted power, performance can be substantially improved only by an improvement in pointing and tracking accuracy, coupled with either larger aperture dimensions or a higher transmitting frequency.
For comparable performance, the aperture diameter of a noncoherent receiver would be about 30 times that of the coherent receiver and therefore unsuitable for a satellite relay station.
Comparison of systems
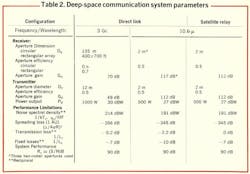
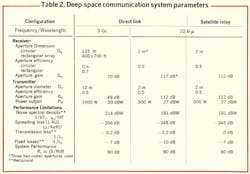
Based on a performance goal of 108 bits per second, three specific systems are compared in Table 2. A signal-to-noise ratio of 10 is adequate for an acceptably low error rate with a suitable modulation code. This goal corresponds to a signal-to-noise bandwidth product of 90 dB.
Parameter values are chosen generally within the practical limitations previously described, and with system and spreading losses as discussed before. The increase in performance over present and planned systems as required to meet the goal is distributed among the two aperture areas and the transmitted power. Equivalent noise performance has already been extrapolated close to the fundamental quantum limit or to a reasonable temperature limit. The specific apportionment of these improvement factors is based on estimates of both development and engineering effort and costs required for their achievement.
Two optical systems are shown in the table: a direct communication link between spacecraft and earth, and a link using a satellite relay station. An eventual choice between the two or between microwave and optical links must depend on realistic systems and cost analyses, which will necessarily be influenced by the results of current and future research programs.
Direct microwave link at 3 Gc
A 90-dB information-rate parameter, R0, = (S/N)B, for the direct microwave link operating at a nominal frequency of 3 Gc is achieved by postulating improved performance of receiving antenna, transmitting antenna, and spacecraft transmitter.
The proposed receiver antenna gain of 70 dB requires an aperture equivalent to a circular antenna diameter of 440 ft (55 percent efficiency) at 3 Gc. (At 2.3 Gc the required diameter would increase to about 580 ft.) The difficulties of implementing such an antenna as a single dish lead to consideration of a distributed array. If a 70-percent aperture efficiency is assumed, a rectangular array for effective operation at zenith angles up to 30 deg latitude and 60 deg longitude would have dimensions of about 400 x 700 ft at 3 Gc (or about 500 x 900 ft at 2.3 Gc). These dimensions are within expected atmospheric correlation lengths so that compensation for atmospheric distortions is unnecessary.
Operation is limited to a maximum zenith angle of 60 deg to avoid excessive, inefficient aperture dimensions; however, this would increase the minimum number of receiver sites for continuous angular coverage from three to four. Note that at the reduced zenith angle, atmospheric background noise will be decreased so that an operating frequency closer to 5 Gc may be favored for the microwave link.
A gain of 49 dB for the spacecraft transmitting antenna corresponds to a diameter of about 12 meters. Since weight added to the spacecraft entails a more than proportionate increase in booster weight, a considerably low performance increase normally would be required of the spacecraft antenna. Nevertheless, techniques being developed for the deployment of antennas after the boost phase of flight permit consideration of larger apertures at high performance-to-weight ratios. Thus, an improvement approaching that of the ground antenna is postulated for the spacecraft antenna.
Transmitter power is taken as 1 kW. An increase in transmitter power to this value involves a related increase in spacecraft power supply and heat dissipation capabilities and, therefore, substantially affects over-all vehicle weight and booster requirements. This output power corresponds to a raw power requirement of about 3 kW, which is not incompatible with spacecraft capabilities estimated for 1980.
Direct optical link at 10.6 μ
This file type includes high resolution graphics and schematics when applicapable.
For coherent reception of a signal arriving at a zenith angle of 70 deg, a receiver aperture of only a half meter (50 percent aperture illumination efficiency) would be expected to suffer a 3-dB loss in aperture gain with typical atmosphere distortions of the signal wavefront. Careful selection of the site and perhaps tower-mounting of the receiver should permit doubling of the aperture diameter for the same over-all aperture efficiency, giving a 60-dB enhancement.
A further 3 dB can be gained by increasing the aperture diameter at the expense of a 50 percent loss in efficiency. For greater diameters, overall aperture efficiency drops rapidly and there is little advantage to further increases. A single-element receiver aperture is therefore limited to about a 2-meter diameter corresponding to a nominal gain of 112 dB but with a 6-dB loss (included among the fixed losses in Table 2) due to atmospheric turbulence.
The gain of the transmitter aperture is limited by the accuracy with which the transmitter can be pointed at the earth station. For an effective pointing accuracy of five μrad, or a minimum allowable beamwidth of ten μrad, the gain is limited to 112 dB, corresponding again to a 2-meter aperture diameter (50 percent efficient).
A transmitter power of 500 W is assumed corresponding at the lower laser efficiency to the same raw power requirement set for the microwave case. On this basis, over-all performance in terms of the information-rate parameter for a single-element ground-based receiver amounts to 85 dB. An additional 5 dB is required to meet the 90-dB goal.
The deficit could be made up in principle by improving spacecraft pointing accuracy from five to three μrad, allowing an appropriate increase in transmitting aperture gain; but in practice, this would require a corresponding increase of aperture diameter to just over 3 meters. More practically, a three-element ground-receiver aperture could be used. Individual aperture elements would be phase-locked to the incoming signal to compensate for the atmospheric phase distortion and the signals would be correlated at the IF frequency. This alternative is given in Table 2.
Satellite relay link at 10.6 μ
Aperture diameter of a satellite receiver is limited by achievable pointing accuracies. However, the pointing problem reduces to a simple closed-loop angle-tracking problem internal to the receiver. Considerably smaller pointing errors can be anticipated for the receiver than for the transmitter, where the detected error angle must be translated to a predicted pointing angle for the transmitter to overcome such problems as bore-sight misalignment and lead angle.
If an achievable rms error of 1.5 μrad is assumed for the receiver tracking angle, a gain of 122 dB should be allowable for the receiver aperture. This corresponds, however, to a diameter of about six meters and requires optical-quality fabrication tolerance of σ/D = 10-7. The fact that such an aperture exceeds the dimensions of the Mt. Palomar telescope should not be used to discount entirely the possibility since, for a monochromatic radiation, focusing techniques such as the use of Fresnel-zone plates might be developed to permit light-weight, space-deployable apertures.
A more predictable solution to the problem, however, would be a receiver aperture of two meters, equal to the spacecraft transmitter aperture, and having a gain of 112 dB.
A transmitted power of 500 W, similar to that for the direct spacecraft-to-earth link, is then required to meet the desired performance goal of 90 dB.
The choice between a satellite-relay and a direct optical communication link reduces essentially to an evaluation of the costs of a satellite receiver (one or at most two required) as opposed to multiple ground-based receivers in widely dispersed locations.
Summary and conclusions
This file type includes high resolution graphics and schematics when applicapable.
Signal coding techniques are available which permit a close approach to the theoretical data-rate limit. Similarly, receiver noise and detection efficiency are approaching reasonable or ultimate limits within the spectral regions of interest except at millimeter and submillimeter wavelengths. Efficient, narrow-band radiative sources of suitable cw power are available in both radio and optical regions of the spectrum except at submillimeter, near-infrared, and visible wavelengths. (Two years ago the entire optical region would have been excluded.) The significant restrictions on system performance are therefore due to external noise sources and atmospheric effects which identify certain favorable regions of the spectrum, and to engineering and technological limitations on aperture gain which determine the achievable levels of performance within these favorable regions.
Galactic noise and atmospheric background tend to define a low noise region between 1 and 10 Gc in good weather, which is narrowed to about 1 to 5 Gc during rain. Above 50 Gc, atmospheric absorption becomes prohibitive to about 12 μ except for a partial window at 94 Gc. Cloud cover extends the blackout through the optical region. Thus, for a ground-based receiver, good performance is limited to the 1-to-10-Gc region and to optical wavelengths. With rain and clouds, the useful frequency band is restricted to 1 to 5 Gc.
Distortions of the incident wavefront caused by atmospheric turbulence limit the effective dimensions, and hence again, of single-element receiver apertures. In the microwave region, gains are limited to about 80 dB; and in the optical region, to about 100 dB. Fabrication tolerances set gain limits on both receiver and transmitter apertures. A given ration of rms deviation in effective path length to aperture diameter yields a gain limit constant with frequency.
In practice, similar tolerance ratios are achievable for smaller diameters so that as aperture dimensions decrease with increasing frequency, an improvement in gain can result. Gain is finally limited at the high-frequency end of the spectrum by need for a beamwidth comparable to expected pointing errors.
The basic limitations on system performance define two spectral regions of interest for a ground-based receiver: one in the microwave region near 3 Gc, another in the optical region near 10 μ. However, since poor weather conditions can effectively black out the entire optical region, the requirement for essentially continuous link operation would require several ground stations at diverse locations to assure good weather for at least one link.
Atmospheric distortions of the wavefront restrict single-aperture receiver diameters in an approximately inverse relationship to frequency. Multi-element apertures are required to provide equivalent performance at higher frequencies. Although for a given performance, over-all receiver aperture area can be reduced in proportion to the increase in gain available from the transmitter aperture, receiver simplicity tends to favor the longer optical wavelengths. The unique availability of an efficient transmitting source at 10.6 μ provides an overriding argument which directs interest to the 10-μ region for an optical communication link employing coherent reception.
For noncoherent reception, receiver sensitivities as limited by thermal or quantum noise are sufficiently below coherent levels to require excessively large aperture areas. Although these “photon buckets” need not be of optical quality, practical limitations on detector size would require fabrication tolerances comparable to those microwave apertures with the additional requirement of a specular surface. Therefore, unless an efficient laser becomes available in the visible region, noncoherent reception is not recommended for wideband communication links.
For a satellite receiver, atmospheric restrictions do not apply. However, the large aperture dimensions appropriate to microwave frequencies, with no appreciable compensating advantages in terms of reduced atmospheric losses and background noise, eliminate consideration of a microwave spacecraft-to-satellite relay link. At the same time, millimeter- and submillimeter-wave regions offer little advantage over the optical region with respect to the state of the art of radiative power sources and detectors. Moreover, the larger apertures required put this region at a comparative disadvantage. The optical region is therefore favored. Gain limitations due to pointing accuracies and the present availability of an efficient transmitting source at 10.6 μ once more direct attention to the 10-μ region.
Three basic system configurations are therefore considered worthy of further investigations. These are:
- Direct microwave, spacecraft-to-earth communication link in the region of 1 to 5 Gc;
- Direct optical link at 10.6 μ employing additional ground stations to assure the necessary weather diversity;
- Satellite relay (one or at most two required) using a 10.6-μ optical link from spacecraft to satellite with a noncritical microwave link for the short link from satellite to earth.
Further research and development are required before detailed analysis can be made to determine the relative costs appropriate to these configurations.
This file type includes high resolution graphics and schematics when applicapable.