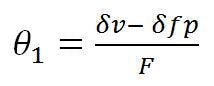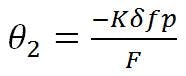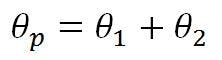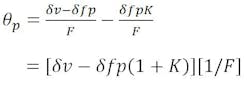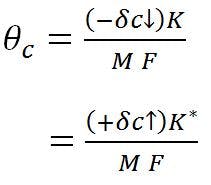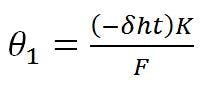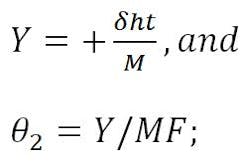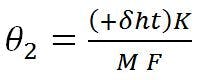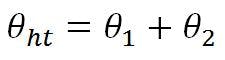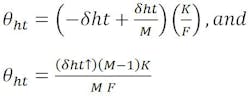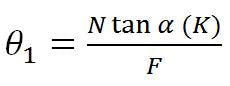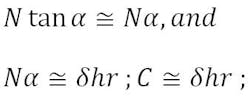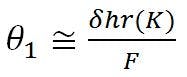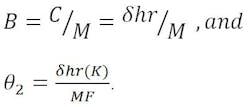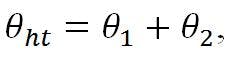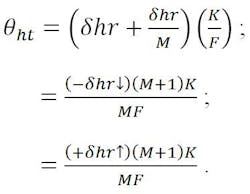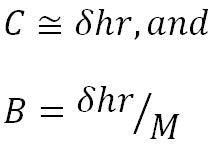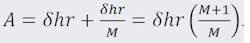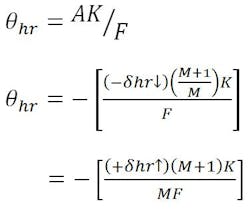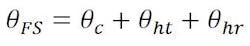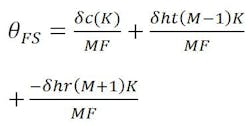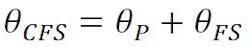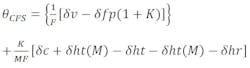Obtaining Beam-Pointing Accuracy with Cassegrain Antennas
August, 1967
Cassegrain antenna specifications never seem to define the specific relationship between reflector deflection characteristics and those of the feed system components. Yet, such relationships seriously affect antenna pointing accuracy. This article defines and develops from a system standpoint these pointing-accuracy interrelations.
Pointing-accuracy factors
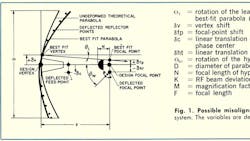
The Cassegrain system geometry is shown in Fig. 1. All possible misalignments (not restricted to the plane of the paper) are indicated. The variables that affect pointing accuracy are: 1. The rotation of the reflector; 2. The translation or lateral displacement of the feed phase center; and 3. The translation and rotation of the subreflector.
Reflector beam deviation analysis
This file type includes high resolution graphics and schematics when applicapable.
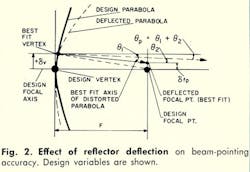
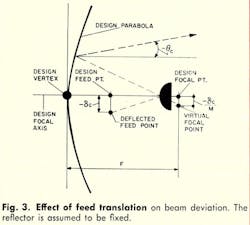
Referring to Fig. 2, the reflector pointing error, θp, results from the anti-symmetrical deflection characteristic of the parabolic reflector. Best fitting of the anti-symmetric deflections of the reflector causes beam shift and beam deviation. Consequently, both vertex translation (δv) and focal point translation (δfp) from the original focal axis occur.
Since the radius of the curvature of the upper half of the reflector for gravity deflections (at the horizon position and in the deflected shape) is less than that of the lower half, the best-fit axis of the entire reflector shifts from the original design focal axis is shown. This effect is also produced by differential wind and thermal loadings and from surface manufacturing and alignment tolerance deviations.
The best-fit rotation of the reflector axis, θ1, is:
Relating the best-fit reflector axis to the design focal axis is accomplished by “translating” the focal point of the best-fit parabola an amount –δfp, which results in a counter-clockwise beam deviation angle (θ2) of:
where K = RF beam-deviation factor. This is the equation normally associated with beam deviation in a focal-point feed system with feed motion.
The resultant beam deviation, θp, is:
Substituting,
This is the equivalent to the best fit or average rotation of the reflector aperture plane from its initial undeflected position.
Feed displacement effects
This file type includes high resolution graphics and schematics when applicapable.
where e is the eccentricity of the hyperboloid.
The displaced (virtual) focal point, due to feed translation, is –δc/M, and the corresponding beam deviation or pointing error equation for feed displacement is:
*Sign Convention: Clockwise beam rotation (upward focal point motion) is positive.
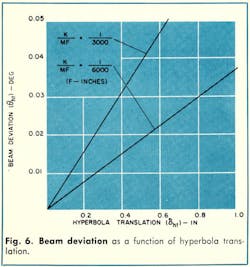
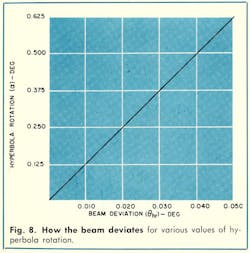
The effect of feed translation on pointing error is shown in Fig. 4. The beam deviation angle, θc, is only slightly affected by displacement of the feed phase center. θc is approximately one-fifth the feed displacement angle or δc/F.
Effects of hyperbola displacement
Like feed displacement, hyperbola-vertex displacement along the focal axis of the design parabola does not affect pointing error or beam deviation, because whatever happens is symmetrical about the RF axis.
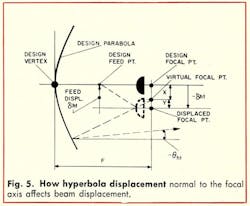
Displacement of the hyperbola vertex normal to the focal axis is reflected as displacement of the source image from the focus of the design parabola (Fig. 5). The beam deviation angle, θht, resulting from this displacement, depends on and is reduced slightly by M, the magnification factor.
The beam-deviation or pointing-error equation is determined by computing the location of the virtual focal point, X, as follows:
With the feed displaced an amount equal to the displacement (-δht) of the hyperbola, the displaced focal and feed points become coincident. The pointing error becomes simply:
A correction must be applied to this equation to relate the displaced feed point to the design focal axis. As before, this is accomplished by “translating” the displaced focal point an amount equal to +δht back to the original design focal axis. This effect is identical to beam deviation due to feed translation. Therefore:
Substituting,
Since
the resultant beam deviation or pointing error equation for hyperbola translation becomes:
From the virtual focal point, (X), the same equation can be derived as follows:
X = -δht + Y.
Substituting,
X = -δht + δht/M
= -δht (M – 1)/M
Since,
Pointing errors from hyperbola rotation
This file type includes high resolution graphics and schematics when applicapable.
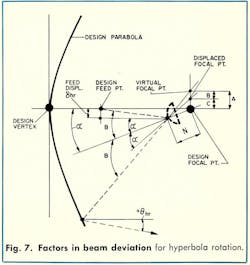
The beam-deviation or pointing-error equation is dependent on the location of the virtual focal point, A. This can be found as follows:
First, displace the feed an amount equal to the displacement of the hyperbola vertex (-δhr).
The initial displaced focal point, C, = N tan α, and the beam deviation angle is:
For small angles,
Therefore,
A correction must be applied to relate the displaced feed point to the design focal axis. This is accomplished by “translating” the displaced focal point an amount equal to +δhr back to the design focal axis. This latter effect is also identical to beam deviation due to feed translation. Therefore:
Since,
the resultant beam-deviation or pointing-error equation for hyperbola rotation becomes:
From the virtual focal point, A, the same equation can be developed as follows:
A = B + C.
Since,
then,
Since,
System analysis
This file type includes high resolution graphics and schematics when applicapable.
The beam-deviation formula for the feed system, θFS, obtained from the combined effects of feed translation (θc), hyperbola translation (θht), and rotation (θhr), is:
Substituting,
where δc and δht, and δhr are positive displacements in the + Y direction (Cartesian coordinate system).
The beam deviation formula for the Cassegrain system as an assembly is:
Substituting,
Once a reflector structure has been designed for minimum weight commensurate with its stress and surface accuracy requirements, its pointing error can be minimized. This can be achieved by the proper selection of deflection characteristics for the feed cone and hyperbola components. This becomes clear once it is realized that feed-cone and hyperbola motions are nothing more than different forms of focal-point motion identical to feed motion for a primary-feed system. Consequently, component weights, surface accuracy, and pointing accuracy can each be optimized individually utilizing the system equations here developed.
Pointing-accuracy criteria for each Cassegrain-system component have been developed. The individual effects can be isolated and the most significant parameters detected.
The most significant parameters that affect beam pointing are the rotation of the parabola and translation of the hyperbola. Feed-cone translation has an approximate 20 percent effect on beam pointing; hyperbola rotation, approximately a 10 percent effect. The magnification factor also has a significant effect.
This file type includes high resolution graphics and schematics when applicapable.