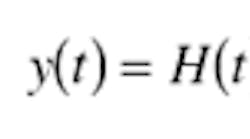Antenna elements arranged in a multiple-input-multiple-output configuration can impact the capacity of a wireless-communications system and combat multipath effects. But one of the keys to improved performance is finding the optimum MIMO layout for a given system scenario, and when it makes sense to stop adding antenna elements and simply optimizing the existing antennas. Last month, this two-part article introduced basic MIMO concepts; this conclusion explains how to calculate the envelope correlation of a MIMO system for a given number of antenna elements.
Thaysen et al.26 related the mutual orientations, the location, and the mutual coupling to the envelope correlation between two identical antennas on an infinite ground plane. They investigated symmetrical as well as asymmetrical coupling scenarios using two identical PIFAs located close to each other on the same ground plane, in order to determine the envelope correlation versus distance for fixed orientations, and the mutual coupling versus rotation of the antennas for fixed distance. The results (simulated using IE3D simulation software37) illustrate how to orientate and locate the antennas in order to minimize the envelope correlation. Two different cases were investigated: one with parallel PIFAs and another with orthogonal orientation as shown in Fig. 3 (the horizontal distance, d, is defined such that d is positive in the case illustrated in Fig. 3(a). For the parallel case with a 10-mm separation, it was found that the envelope correlation is ρe = 0.8 and simply by rotation of one the antennas 180 deg., the envelope correlation decreases to ρe = 0.4. Similar results were seen for the orthogonal antennas setup Fig. 3(b)> where the envelope correlation decreases from ρe = 0.5 to ρe = 0.25. For the orthogonal setups, the highest envelope correlation is obtained when the open end and the feed line are vertically on line.
Those researchers found that the deviation in the center frequency (min. |S11|) was most affected in the case of parallel antennas, each having the feed point in the same end, where a change of 12 percent was observed. In the other scenarios (the two orthogonal cases), the change was less than 2 percent compared to a single PIFA element. The maximum envelope correlation of ρe = 0.8 was obtained for the parallel setup, when the antennas are vertically overlapping each other, and highest value was obtained for the setup having the feed line in same ends.26
Also, an almost exponential relation between the mutual coupling and the envelope correlation was found.26 A mutual coupling limit of –10 dB was found in these studies. Below that limit, the envelope correlation was almost constant, being ρe = 0.15, and therefore any effort in decreasing the mutual coupling could be limited to this level.
Placing the antennas on a finite ground plane affects their performance.6 For the designs illustrated in Fig. 4, the antennas were optimized in terms of the input impedance and bandwidth of the planar inverted-F antenna (PIFA) (e.g., by changing the distance between the feed and the ground contact) dependent on the location of the PIFA on the ground plane. The best antenna configurations were chosen from some performance metrics (correlation and bandwidth). However, the proximity effects of a mobile telephone's cover, the artificial hand, and the head should be included in the analysis.8 Hence, the results concerning the optimal configurations might differ somewhat when such effects as the cover, hand, and head are taken into account.
For MIMO application, where low envelope correlation is essential, the location and orientation of the antennas should be optimized not only with respect to envelope correlation but also with respect to bandwidth. It has been found that for the two-antenna configuration, optimal locations and orientation with respect to the MIMO performance, i.e., bandwidth and envelope correlation between the antennas, are not necessarily the ones with the lowest envelope correlation.6 A certain bandwidth is required as well. Taking both the envelope correlation and bandwidth into account, it was found that configuration B4 yielded the best performance. Here, the bandwidth is 12.2 percent centered around 1.79 GHz; the envelope correlation is below 0.1, and the strongest mutual coupling is –7.7 dB.
From the 15 different two-antenna configurations investigated by Thaysen et al.,6 the relation between the envelope correlation and the mutual coupling indicated that low mutual coupling leads to low envelope correlation. However, low envelope correlation does not necessarily come from low mutual coupling. Also, it was observed that low mutual coupling results in low bandwidth, primarily caused by the poor impedance match (high reflection coefficient) of the antennas in these configurations. High bandwidth occurs in the configurations that also yield high mutual coupling. Thaysen et al.16 concluded that high mutual coupling reduces the freedom in choosing an optimal configuration.
Taking the increased complexity into account, it is possible that careful optimization of a given number of antenna elements is preferred compared to a scenario where an extra antenna element has been added.38 In\ ref. 6, evaluation of the MIMO system was based solely on the antenna performance, such as the envelope correlation, mutual coupling, resonance frequency, bandwidth, and radiation efficiency of the antenna elements, especially with a focus on the envelope correlation and the bandwidth. However, the real advantage of a MIMO should be the improvement in capacity. Thus, the capacity should be evaluated. To determine the full advantage, capacity should be evaluated in a multipath environment.8
To calculate the capacity of a MIMO system, information is needed for both the propagation environment and the antenna configurations. Realistic evaluation of MIMO antenna structures requires multielement propagation measurements with MIMO antenna configurations. One way to obtain these multielement propagation measurements is to characterize an actual prototype in real scattering environment. This, however, is a very time-consuming process. Moreover, the entire measurement must be repeated for all MIMO antenna proposals.
Thaysen et al.8 presented measurement-based results for evaluating MIMO antenna performance. The results were produced by merging the complex radiation pattern of the antennas under test with a MIMO coupling matrix. The MIMO coupling matrix represents a small macrocell MIMO environment measured in downtown Helsinki (see for example, ref. 39 for maps). The MIMO coupling matrix was measured by Dr. Vainikainen's group at Helsinki University of Technology.39, 40
These multielement propagation measurements enable a combination of measured propagation paths with the radiation pattern of the antenna elements.39, 41 However, this requires the extraction of the full double-directional propagation channel parameters. The measurement setups consisted of a channel sounder for measuring the spatial and temporal characteristics of the radio channel, a linear transmitting antenna array, and a spherical receiving antenna array, both employing dual-polarized patch antennas.42, 43
Page Title
The transmit antenna array consisted of eight directive and dual-polarized antenna elements separated by one-half wavelength (0.5 λ) from which different numbers of elements were selected in the post processing of the measurement data. The transmitted power is limited to +26 dBm.41, 44 The spherical receiving antenna array was formed by 32 elements, each similar to the elements in the transmit array. The elements that are located on the sphere were used at the receiving mobile station. One dual-polarized element consists of two orthogonal channels, i.e., and -polarized feeds41, 44 The rootmean-square (RMS) error of the incident-angle measurement is approximately 1 deg.45 Originally, this measurement system were developed for a SIMO system, but was extended to MIMO measurements.46
The signal at the base station is related to the signal at the receiving signal mobile station through the matrix H representing the transmission at a certain time and spatial location of the antennas in the multipath environment via:
where:
y(t) = the transmit signal at the base station given by the expression:
and
s(t) = the signal at the receive signal at the mobile station.
Matrix H is found from:
where:
αi,j = the complex transmission coefficient from antenna i to antenna j.
These results are restricted to frequency flat fading channels, and therefore the corresponding input–output relation can be simplified to B=H(t)A, where H is the narrowband matrix that describes the complex channel from the mth transmit antenna to the nth receive antenna in a (m, n) MIMO antenna system, at a time t and the spatial location of the antennas in the multipath environment. The capacity of the MIMO system can then be calculated with a combination of the measured radiation patterns of the antennas and the measured MIMO channel. In order to calculate the capacity, measurements must be of the radiation pattern of a single element when all the other elements are present (but terminated with loads representing the source impedance on their ports). In ref. 8, the complex radiation patterns are measured in an anechoic chamber. Measurements were made both in free space and in more realistic environments, i.e., where the antennas are mounted next to an artificial hand and head to determine proximity effects. In order to obtain as realistic results as possible for the MIMO evaluation, results included the measured macrocell MIMO environment combined with the radiation pattern from the proposed MIMO system antennas.
The Shannon capacity for a traditional channel with only one transmission channel used for data transmission in a SISO system is:47
where:
SNR = the signal to noise ratio. Without any knowledge of the channel characteristics, the only feasible way to distribute the transmit power is to share it equally on all the transmit antenna elements.3 The capacity of such a MIMO system with unknown channel and equal power distribution is defined as:2-4
where:
I = the identity matrix,
(*) = transpose conjugate, and
H = the MIMO system channel matrix.
It has been demonstrated that the capacity in Eq. 9 grows linearly with m = min(M, N), rather than logarithmically as in the diversity case.3,4
This capacity formula is valid under narrowband assumptions, i.e., with a frequency-flat fading MIMO channel.3 If the channel is frequency-selective, matrices H depend on the frequency as well. In such a case, one should integrate over the transmitted bandwidth, for calculating the capacity in such case.27
Assuming that the channel is known at the transmitter, the signal transmission is divided over the transmit antennas in such a way as to optimize the channel capacity. The total transmit power is divided such that a greater portion goes to the channels with higher gain, and lesser or even none to the channels with smaller gains.3 This technique is known as water filling.3
Page Title
For a transmitter where there is full knowledge of the MIMO channel, the maximum achievable capacity corresponds to the water-filling solution. In practice, the available knowledge may only be partial, due to the time selectivity of the channel, and delay or absence of feedback from the receiver. However, exploiting even this partial knowledge leads to a significant improvement when compared to the capacity without any channel knowledge.5 Water filling has a significant advantage over equal power schemes at low SNR. At low SNR, the water-filling technique finds the largest eigenvalues for H and sends the entire power trough one single mode (channel). At an intermediate value of SNR, the water filling still improves the capacity over the equal power schemes. However, this advantage decreases with increasing SNR. At intermediate SNR the water-filling technique uses L antennas where 1 < L < min(N, M). At high values of SNR, the water-filling schemes functions almost as equal power schemes and the advantage over the equal power scheme decreases.5
Reference 8 shows experimental results of the capacity and the diversity gain for three simple yet realistic two- and three-antenna configurations as illustrated in Fig. 5. The channel data were measured in a small macrocell environment in downtown Helsinki. The results are for both the free-space radiation pattern as well as the talk position radiation pattern, i.e., beside an artificial hand and head. In ref. 8, the channel was unknown at the transmitter, and hence the capacity is calculated using equal power allocation, i.e., using Eq. 9.
The proposed two-antenna configuration (see Fig. 5a) yielded a 50-percent outage channel capacity C0.5 in the (2, 2) system of 5.0 b/s/Hz calculated using the free-space radiation patterns. A slight decrease of 0.1 b/s/Hz for the radiation patterns obtained in talk position beside an artificial hand and head is seen. This discrepancy comes from the ratio between the peak total efficiency for Antenna 1 and Antenna 2 that is somewhat lower compared to the free-space results. The average received SNR was chosen to be 10 dB in both cases.
The gain from using more than one antenna is calculated as the difference between the power after maximum ratio combining (MRC) and the stronger branch power (Br1 are related to Antenna 1 and Br2 are related to Antenna 2) at the level that 90 percent of the signals exceed.40 This result is strongly affected by branch power difference. As shown in Fig. 6(b), the MRC is 4.8 dB higher than Br1. At a probability level, p, of 50 percent, the difference between Br1 and Br2, (ΔBr2-Br1) is 2.8 dB. The fact that the branch power of Antenna 1 is the highest seems reasonable when taking the measured total efficiency into account; since Antenna 1 has the highest total efficiency.8
The three-antenna configuration, (3, 3) MIMO system, has a 50-percent outage channel capacity, C0.5, of 7.1 b/s/Hz using the free-space radiation patterns Fig. 5(b)>. Even though the branch power of antenna 2 is 16.8 dB below the MRC, it improves the capacity by 1.5 b/s/Hz compared to the (2, 2) MIMO configuration. The capacity can be further optimized by designing multiantenna systems such that the efficiencies of the different antennas are somewhat comparable. The same trends are observed when cramming the antennas into a mobile telephone Fig. 5(c)>. The fact that the measured free-space radiation efficiency is approximately 20 percent lower when incorporating the antennas into a mobile telephone does not affect the free-space capacity, which is unchanged 7.1 b/s/Hz.8 This stems from the rather unchanged ratio between the peak total efficiencies measured in free space.
When the three antennas are incorporated into a telephone, the measured radiation efficiency, when placed next to an artificial hand and head, was between 4 and 14 percent from 1.7 to 1.9 GHz. On average, this is lower than the three-antenna configuration mounted on a ground plane. But the efficiency ratios between the antenna elements are diminished by the extremely low radiation efficiency of antenna 2 (below 2 percent). Thus, the capacity is 0.5 b/s/Hz above the three-antenna configuration, which is not mounted in a mobile telephone.
The theoretical linear relationship between capacity and the number of antenna elements as forecasted in the early work related on MIMO2-4 was verified experimentally by Thaysen et al.8 It was shown that the capacity increases with increased SNR (Fig. 7). At low SNR (i.e., below 5 dB), the difference in using three antennas instead of two is low. At SNR = 0 dB, the difference is 0.5 b/s/Hz, the talk-position capacity of 1.6 b/s/Hz being the lowest. The gain by using an extra antenna having a SNR of 50 dB is a talk-position capacity of 43 b/s/Hz, being 14 b/s/Hz higher than the capacity obtained using the two-antenna configuration. The Shannon limit of the capacity of the SISO system at an SNR of 50 dB is 16.6 b/s/Hz. This is approximately one-half the (2, 2) capacity and a third of that obtained using a (3, 3) MIMO system. Similar trends could be found in refs. 3, 5, and 9.
The MIMO system is based on two or more subchannels transferring data simultaneously at the same bandwidth. The effect of increasing the number of transmit elements on the average capacity for the three different configuration used here are discussed by Thaysen et al.8 Simply by adding more elements at the transmit antenna configuration the capacity could be increased. For the two-antenna configuration proposed by Thaysen et al.,8 the talk position capacity is increased from 4.1 b/s/Hz for the simple diversity setup (1, 2) to 4.9 b/s/Hz for the full (2, 2) MIMO system. The capacity reaches 5.2 b/s/Hz in the case of three transmit elements and two receive elements (3, 2). This means that the extra transmit antenna yields an extra 0.3 b/s/Hz. For the three-antenna configuration mounted inside a mobile telephone, the talk position capacity increases from 4.7 to 8.2 b/s/Hz, when increasing the numbers of transmit elements from one to seven. Above four transmit elements, the capacity increase is less per transmit element as the capacity increase per transmit element below three. From one to four transmit antenna elements, the talk position capacity increases from 4.7 to 7.4 b/s/Hz, as compared to an increase of0.8 b/s/Hz for the last three antennas. The most significant improvement is for an increase from one to two transmit elements, i.e., from a (1, 3) to a (2, 3) MIMO system. Bearing in mind that capacity grows linearly with m = min(M, N) and logarithmically in the diversity case, this is in accordance with theory.3,4 Sulonen et al. have obtained similar trends.44
Recently, Molisch et al.38 have shown a MIMO system that takes simple diversity into account, i.e., in either one or both of the link ends. This setup uses L antenna elements from the (N, N) MIMO system, in this way yielding a reduced MIMO system which has a reduced complexity compared to a full (N, N) MIMO system. Among others, Vaughan has shown that transmit or receive diversity can improve link quality.48
Lebrun et al.49 suggested two methods for complexity reduction; one based on the SNR and another based on signal strength. The results presented by Lebrun et al.49 are based on a known channel with water filling. In ref. 8, capacity results are calculated under the assumption that the channel is unknown at the transmitter, and that the power is distributed equally among the antenna elements. Adding an extra antenna increases the capacity8, 44; however, this decreases element performance due to reduced space between antenna elements.6 Thus, the benefit of the extra antenna element might be reduced compared to the theoretical capacity increase. Therefore, a trade-off exists between capacity and increased MIMO system complexity when an antenna element is added. Taking the increased complexity into account, careful optimization of a given number of antenna elements may be preferred to the addition of an antenna element. Figure 8 shows the capacity for different numbers of transmit elements for the two- and three-antenna configurations.
Thaysen et al.8 also studied the effects of a reduced MIMO system with an unequal number of antennas in the receiver and transmitter. They concluded that, from a capacity standpoint, it is better to have a full (2, 2) MIMO system (C0.5 of 4.9 b/s/Hz) than a transmit diversity system of (1, 3) (C0.5 of 4.7 b/s/Hz). They learned that it is better to have an extra receive antenna, i.e., (TX, RX) = (2, 3), rather than an extra transmit antenna (3, 2). The receive diversity setup has a capacity of 5.8 b/s/Hz which is 0.6 b/s/Hz higher than the transmit diversity setup. This is in accordance with the results described by Foschini et al.3 For a known channel, the receive diversity setup yields the same capacity as the transmit diversity setup.5 Bearing in mind that the hardware complexity of a MIMO system increases with the number of antennas, antenna selection could be used as a simple method to increase the capacity of a MIMO antenna configuration with minimal added hardware complexity.
Page Title
ACKNOWLEDGMENTS
This work was supported by Nokia Denmark. The authors wish to thank Elna Sørensen from Technical University of Denmark for proofreading the article. Thanks are also due for valuable comments from Kimmo Kalliola from Nokia Research Centre, Helsinki, Pasi Suvikunnen and Dr. Petri Vainikainen from Helsinki University of Technology, Dr. Jørgen Bach Andersen from Aalborg University, and Dr. Erik Bruun from Technical University of Denmark.
REFERENCES
For references 1-36, see p. 78 of May 2007 issue of Microwaves & RF or go to www.mwrf.com/Articles/Index.cfm?ArticleID=15565&pg =3
37. Internet: www.zeland.com.
38. A.F. Molisch and M.Z. Win, "MIMO systems with antenna selection," Microwave Magazine, IEEE, Vol. 5, No. 1, pp. 46-56, 2004.
39. K. Sulonen, P. Suvikunnas, J. Kivinen, L. Vuokko, and P. Vainikainen, "Study of different mechanisms providing gain in MIMO systems," Proceedings of the IEEE 58th Vehicular Technology Conference, 2003.
40. P. Suvikunnas, K. Sulonen, J. Villanen, C. Icheln, J. Ollikainen, and P. Vainikainen, "Evaluation of performance of multi-antenna terminals using two approaches," Proc. IEEE Instrumentation and Measurement Technology, IMTC 2004, pp. 6, Italy, 2004.
41. K. Kalliola, H. Laitinen, K. Sulonen, L. Vuokko, and P. Vainikainen, "Directional Radio Channel Measurements as Mobile Station in Different Radio Environments at 2.15 GHz," 4th European Personal Mobile Communications 2001 -Conference, Austria, 2001.
42. J. Kivinen, P. Suvikunnas, D. Perez, C. Herrero, K. Kalliola, and P. Vainikainen, "Characterization system for MIMO channels," Proceedings of the 4th International Symposium on Wireless Personal Multimedia Communications, 2001, pp. 159-162.
43. K. Kalliola, H. Laitinen, L. Vaskelainen, and P. Vainikainen, "Real-time 3-D spatial-temporal dualpolarised measurement of wideband radio channel at mobile station," IEEE Transactions on Instruments and Measurements, Vol. 49, pp. 439-448, 2000.
44. K. Sulonen, P. Suvikunnas, L. Vuokko, J. Kivinen, and P. Vainikainen, "Comparison of MIMO antenna configurations in picocell and microcell environments," IEEE Journal on Selected Areas in Communications, Special issue on MIMO systems and Applications, Vol. 21, No. 5, pp. 703712, 2003.
45. K. Kalliola, H. Laitinen, L. Vaskelainen, and P. Vainikainen, "Real-time 3-D spatial-temporal dual-polarized measurement of wideband radio channel at mobile channel," IEEE Transactions on Instruments and Measurements, Vol. 49, pp. 439-446, April 2000.
46. J. Kivinen, P. Suvikunnas, D. Perez, C. Herrero, K. Kalliola, P. Vainikainen, "Characterization system for MIMO channels," in Proceedings of the 4th International Symposium on Wireless Personal Multimedia Communications, Aalborg, Denmark, 2001, pp. 159-162.
47. C.E. Shannon, "A mathematical theory of communications: Parts I and II," Bell System Technical Journal, Vol. 27, pp. 379–423, 623–656, 1948.
48. R.G. Vaughan, "Signals in Mobile Communications: A Review," IEEE Transactions on Vehicular Technology, Vol. 35, pp. 133–145, 1986.
49. G. Lebrun; S. Spiteri, and M. Falkner, "MIMO complexity reduction through antenna selection," Proceedings of the Australian Telecommunication Cooperative Research Center, ANNAC ‘03, pp. 5, 2003.