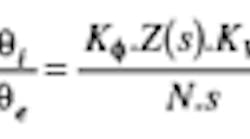Dr. Mohammed Feham and Dr. Mohamed Kameche also contributed to this article.
Frequency synthesizers are critical components in modern mobile-communications systems, powering both transmitters and receivers. Typically, they are designed with a phase-locked-loop (PLL) approach.1 To demonstrate the effectiveness of this synthesizer architecture for one of the more challenging mobile wireless-communications formats, DCS1800, the authors designed and simulated a PLL frequency synthesizer for use in a DCS1800 base station. The base station operates in the receive band of 1805 to 1880 MHz and the transmit band of 1710 to 1785 MHz. The simulation considers the noise effects on each component in the frequency-synthesizer design and the impact of phase margin on system performance.
The frequency-synthesizer design consists of a phase-frequency comparator followed by a charge pump, a loop filter, a voltage-controlled oscillator (VCO), and frequency dividers (Fig. 1). The charge pump converts the logic states of the detector into analog signals appropriate for controlling the VCO. In its off state, the charge pump and the input section of the synthesizer must exhibit extremely low leakage, otherwise voltage integration will occur at the loop filter between phase comparator events.
PLLs are most commonly used in frequency synthesizers, where a range of output frequencies is generated from a single stable reference frequency. This is done my means of a variable ratio divider in the feedback path. The frequency or channel to be synthesized is performed while acting on the ratio of division N (Fig. 1). Because its phase detector is nonlinear, a PLL is primarily considered a nonlinear device.
Figure 2 shows a linear mathematical model representing the phase of the PLL in its locked state,2 where KØ is the phase detector/charge pump gain, Z(s) is the transfer function of the loop filter, N is the main divider ratio, and KVCO is the gain of the VCO. The phase of the oscillator, θ0, is compared with the reference, θr, and adjusted until the difference is zero. Parameters θi and θe are the opposite and the error phases, respectively.
The PLL phase-transfer functions are shown in Eqs. 1 and 2. The open-loop gain is:
The closed-loop gain is:
Since the design of the loop filter is the most critical part of the synthesizer, it will be the primary focus of this article.
The phase detector's outputs are associated with different signals by the charge pump. Each signal is applied to a lowpass filter so that the output voltage of the phase detector does not vary too quickly. Figure 3 shows the standard passive third-order charge-pump loop filter used in PLL frequency synthesizers. The lowpass filter effectively suppresses spurious signals produced by the phase detector so they do not cause unwanted frequency modulation in the VCO. The delay time of the filter, however, can result in degraded transient response and a limit in the switching speed of the frequency synthesizer.3
The transfer function of the third-order loop filter in Fig. 3 is given by:
where Zfil2(s) describes the transfer function of the second-order loop filter given by:
If a temperature-compensated crystal oscillator (TCXO) is used in the PLL synthesizer design, the manufacturer's phase-noise data should be obtained so that reference values can be used with the models. Reference oscillator noise, Ntcxo(f), can be expressed by4:
The VCO noise can be modeled as a simple approximation inversely proportional to the offset frequency from the carrier. The noise of the VCO is effectively highpass filtered by the PLL, providing rejection of phase noise or phase error within the loop bandwidth, although VCO noise well outside of the loop bandwidth is unaffected. The VCO noise is given by5:
It should be noted that the noise generated by the lowpass filter's resistances can affect the input of the VCO even if the PLL is not connected (closed). Active devices, such as opamps, and resistors produce noise voltages. In the case of an operational amplifier, the noise should be specified. In the case of a resistance, this noise voltage is defined by the thermal noise produced by the resistance. The thermal noise produced by a resistance is:
where:
T0 = the ambient temperature (equal to 300 K),
K = Boltzman's constant, and
R = resistance.
Figures 4 and 5 show, respectively, noise models for resistances R2 and R3 as being equivalent sources of noise voltage appearing in series with each resistance. Since the noise sources are not correlated, each resistance must be analyzed separately and the effects added afterward. The derivation of the real voltage of noise versus the input frequency at the VCO's tuning port is based on the basic circuit using models of Figs. 4 and 5.
The phase noise added to the output of the PLL by each resistance is given by the following equations:
where:
mR2(f) = the modulation index according to the frequency for resistance R2 and
mR3(f) = the modulation index according to the frequency for resistance R3.
Page Title
The author's PLL frequency synthesizer was designed for use in a DCS1800 base station. One of the essential components in the PLL design was a model LMX2326 programmable frequency synthesizer from National Semiconductor (www.national.com). The VCO used with the design was capable of generating +7 dBm output power with a 50-W load; it exhibited tuning sensitivity of 30 to 60 MHz/V. The VCO's tuning sensitivity is very important for determining the loop filter parameters. For the reference oscillator, a TCXO was used. It provided a stable output at 10 MHz and phase noise of –110 dBc/Hz offset 10 kHz from the carrier. The LMX2326 provides the feedback tuning voltage for the VCO, ultimately generating a stabilized output signal for use as a local-oscillator (LO) signal in a DCS1800 base station.
The PLL's serial control data travel by means of a three-wire interface (with data, enable, and clock signals) connected to a laptop computer controller and parallel port cable. For the simulated synthesizer in a DCS1800 application, the RF output is locked at 1810 MHz (fVCO) with 200-kHz channel spacing. The reference oscillator is 10 MHz (fTCXO) and the prescaler value (P) is 32. When programming the LMX2326, the desired frequencies and mode of operation should first be determined. The serial data input can then be set to control the 14-b resolution of the R counter and the 18-b resolution of the N counter.
For this DCS1800 base-station application, the values of the R and N counters, respectively, were set as R = fTCXO/ fcomparison = 50 = 00000000110010b and N = fvco / fcomparison = 9050. The calculated value of N, and the value of P, can be used to determine the values of A and B where A and B are both integer values:
N = P X B + A
where:
B = the divisor, and A = the remainder.
Therefore:
B = div (N/P) = div(9050/32) = 282= 0000100011010b
and
A = N – (B X P) = 26 = 11010b
Figure 6 shows the Bode plot for the PLL's open-loop transfer function, where the unity-gain frequency is 10 kHz and the phase margin is 56.8 deg.
Figure 7 represents the response of the closed-loop transfer function. The flat 0-dB region is defined as the loop bandwidth. The input phase variation within the loop bandwidth is reproduced at the output, and the input phase variation outside the loop bandwidth is suppressed because of the negative gain.
Figure 8 illustrates filter transfer functions. Compared to a second-order filter, it is apparent that the gain of the third-order loop filter is increased and the phase margin is reduced. Increasing the loop bandwidth will reduce the lock time, but the filter bandwidth should not be important to avoid significantly increasing the risk of instability. In practice, the most commonly used filter used is the second-order type.
Figure 9 shows the resistor noise contributions at the output after PLL's highpass error is included. These results confirm that the resistor noise contributions to the synthesizer's output are relatively small. Figure 10 shows the phase noise for each component (TCXO, phase detector and VCO), and the total noise. These results show that, inside the loop bandwidth, the noise level of the reference oscillator is more significant owing to the fact that the gain of the closed-loop transfer function is high inside the loop bandwidth, falling quickly outside the loop bandwidth.
For a stable loop filter with realvalued (positive) components, it was necessary to design the synthesizer with a phase margin greater than 0 deg. and less than 90 deg. So far, it has been assumed that the goal has been to minimize the spurious responses and the lockup time. Figure 11 shows the PLL transient response versus phase margin with a third-order filter and frequency switching in 50-MHz steps.
Because the PLL may be modulated with information in an actual application, it is critical to make the loop filter response as flat as possible. Alternately, a design objective is to minimize the amount of peaking in the filter response and minimize the root-mean-square (RMS) phase error. For these purposes, it makes sense to design for as high a phase margin as possible. Figure 12 shows the results of using a third-order loop filter with a loop bandwidth of 10 kHz.
Regarding higher phase margins, the peaking seen on a spectrum analyzer with some PLL synthesizers is generally due to the peaking when the VCO is highly filtered by the PLL's loop filter, causing the rejection of phase noise or phase errors in the filtered bandwidth. Designing for higher phase margins helps to suppress the VCO noise at the loop bandwidth (Fig. 13). In order to ensure the precision of the PLL synthesizer design, an accurate estimation of the loop filter should be used. Figure 14 shows the output spectrum of the PLL synthesizer with an optimal loop filter design.
The synthesizer design yielded an output spectrum with noise density of –69.5 dBc/Hz at multiples of the comparison frequency. The frequency switching speed for a change of 50 MHz was about 250 µs. The root-mean-square (RMS) phase noise was 0.037 rad and the signal-to-noise ratio was about 31.23 dB, making the basic design suitable for a wide range of modern communications systems.
REFERENCES
- S-J. Lee, B. Kim and K. Lee. "A Fully Integrated LowNoise 1-GHz Frequency Synthesizer Design for Mobile Communication Application," IEEE Journal of Solid-State Circuits, Vol. 32, No. 5, May 1997, pp 760-765.
- David Vye, "Performing Transient Analysis on PLL Frequency Synthesizers," Microwave Journal, Vol. 45, No. 1, January 2002, pp. 62-79.
- Akihiro Kajiwara and Masao Nakagawa, "A New PLL Frequency Synthesizer with High Switching Speed," IEEE Transactions on Vehicular Technology, Vol. 41, No. 4, November 1992, pp. 407-413.
- L. Lascari, "Accurate Phase Noise Prediction in PLL Synthesizers," Applied Microwave and Wireless, Vol. 12, No. 2, 2000, pp. 30-38.
- Eric Drucker, "Model PLL Dynamics And Phase-Noise Performance," Microwaves & RF, Vol. 39, No. 2, February 2000, pp. 73-82.