Measurements of electromagnetic (EM) emissions, such as spurious and spectrum emission mask (SEM) measurements, are essential to the effective management of the limited communications frequency spectrum. Wireless standards specifically call out acceptable levels and require the use of emissions measurements to quantify the undesirable signals and potential interference. Unfortunately, these measurements can be slow and are prone to error due to incorrect assumptions about different interference types and analyzer behavior. By understanding instrument limitations, more meaningful emissions measurements are possible. Some methods will be presented to perform these measurements faster and/or with more accurate results than generally accepted techniques.
Interference can come in many forms, characterized by their statistical distribution. One form of this is whether or not they are bursted (intermittently in-place when the transmitter is keyed on). When measuring burst-type signals by means of gated spectrum analysis, the effect of bursting becomes irrelevant to the measurement. The other characterization of their statistics is whether or not the probability density function (PDF) of the amplitude envelope is constant (like a CW signal). Although signals can exist with any PDF shape, this article will only consider the two most likely PDFs: CW-like and noise- like signals.
Single-carrier digital communications signals are noise-like when observed in a bandwidth that is narrow compared to the symbol rate. Orthogonal-frequency-division-multiplex (OFDM) digital communications signals are noise-like when observed with a bandwidth that is large compared to the subcarrier spacing. In both of these cases, the signal is noise-like because the total signal analyzer resolution-bandwidth (RBW) filter response includes the sum of many random responses.
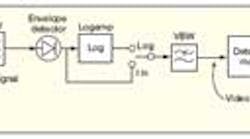
The standards for spurious emissions for all common radio formats are based on ITU recommendation ITU-R SM.329. This document calls for "RMS detection" in measuring signals. This requirement is meant to describe how the signal is to be measured using a measuring device (such as a signal analyzer). However, a significant disparity between the definitions of "detection" used by RF engineers and signal-analyzer users must first be addressed. Figure 1 can be useful in resolving these misunderstandings.
In Fig. 1, an envelope detector block and a detector mode block are featured. The first is one with which most RF engineers are familiar. It converts an intermediate-frequency (IF) signal to a video signal that is proportional to the voltage of the envelope of the signal at the input port. The envelope detector has no user controls, so the user interface never needs to refer to it. There is, then, no ambiguity in the user interface over the use of the word "detector" to refer only to the "detector mode" block. The detector mode block is used to convert a continuous amplitude-versus-time signal into discrete array elements (often called "buckets" or "pixels") of a digital-display spectrum-analyzer trace. This detector may be set to any of many choices, such as peak (the highest level within the duration of a display point) and sample (the level at a single instant in that duration).
One form of detector available in most modern signal analyzers is variously called the "average" or "RMS" detector. This detector measures the root-mean-square of the envelope voltage during the bucket. The root mean square measurement means that we find the square of the signal voltage, take its mean (average it for the duration of one bucket) and take the square root of the result to put it back into voltage form again. Note that the "mean" part of RMS is why some manufacturers call this an "average" detector. It would be natural for the user to assume a standards requirement for "RMS detection" would be calling for the use of the "RMS detector," but this can be a dangerous oversimplification.
Page Title
It can be useful to understand how a signal analyzer responds to noise-like and CW-like signals, subject to three controllable signal-analyzer parameters: averaging scale, noise bandwidth, and sweep rate (defined as span divided by sweep time). When a CW-like signal is envelope-detected in a system such as that shown in Fig. 1, the input to the video-bandwidth (VBW) filter is constant, and the VBW filter has no effect. In contrast, when the input signal is noise-like, the VBW filter averages the signal, reducing its variance.
If a noise-like signal is measured and observed on a linear scale (linear in terms of its voltage, not its power; note that the envelope detector produces a signal proportional to the voltage), the PDF of the noise is the well-known Rayleigh distribution (Fig. 2). On a logarithmic (decibel) scale, the PDF is a less-well-known function usually called the "log-Rayleigh distribution." On a power scale (or proportionally, a voltage-squared scale), the PDF is also known.
In Fig. 1, the choices for setting the scale on which the noise is filtered by the VBW filter are logarithmic (in dB) and linear (in V); power (in RMS V) is not shown. Some analyzers offer "average type" or "average and VBW" type keys that control the averaging scale for the VBW filter. A technique to be described can only be used in these analyzers. In such analyzers, the envelope detector, log/lin switch, and VBW filter are reconfigured as shown in Fig. 3.
When a CW signal is filtered, the result will be independent of the scale on which the filtering occurs; the output signal will be the same whether voltage, power, or log filtering is used. When filtering any signal that varies, such as a noise-like signal, the scale will affect the result. The average of the voltage of a noise-like signal (in other words, a signal with a Rayleigh distribution) is well-known to be 1.05 dB lower than the average of its power; the average of its log is 2.51 dB lower. The only way to accurately measure the average power of a signal with unknown statistics is to average its power on a power scale.1 (Additional resources on spectrum analysis can be found in refs. 2-5.) When a standard for emissions calls for "RMS detection," it means the results should be averaged on an RMS voltage scalei.e., power scaleas performed by the system in Fig. 3.
When a CW signal is measured, the peak response on a signal analyzer display is independent of the RBW filter. But when a noise-like signal is measured, the power is proportional to the bandwidth. The "noise bandwidth" of a filter is defined such that the output power is given by the product of the noise bandwidth and the spectral density of the noise.
The noise bandwidth of filters is usually not the same as their "name." Common signal analyzer practice has been to name the RBW filters by their -3-dB (half-power) bandwidth. For the most popular spectrum analyzers of the 1990s, the filters were four-pole synchronous-tuned designs, with a noise bandwidth 1.128 times (+0.52 dB) their -3-dB bandwidth. The most popular signal analyzers at present use close-to-Gaussian digital RBW filters with a ratio of noise-bandwidth to -3-dB bandwidth of 1.056 (+0.24 dB). Many standards for emissions are based on "RBW filters" and thus are ambiguous to the level of the difference between these two alignments (0.29 dB). These standards are not ambiguous for CW-like interference signals. (This ambiguity is mentioned here, but will not be resolved in this article.)
Page Title
When a CW signal is measured with a sweeping local oscillator (LO) and finite RBW and VBW filter bandwidths, the sweep rate of the LO affects how close to full response the filter response is allowed to approach. In practice, given the likelihood of noise-like signals needing smoothing, the sweep-rate limitations for CW-like signals do not constrain the sweep time.
The other type of analyzer detector might be called a "display detector" or "bucketizing detector," but the user interface simply calls it "the detector." This detector must be present in the analyzer because the sample density of the analyzer trace might be much lower than the density of data from the measurement chain, violating the Nyquist criterion for sampling data. This type of detector may exist as a peak detector or root-mean-square (RMS) or average detector.
The peak detector simply reports the highest result during the bucket. This detector is an excellent choice for conformance-to-standards measurements, of course, because it will unfailingly report any signal that is higher than a limit, whether that emission is CW-like or noise-like. Since it will report the peak of any noise-like signal, it requires considerable averaging (such as VBW filtering) to reduce the risk of reporting an instantaneous above-limit emission which is actually within limits on average. For example, the top of Fig. 2 shows that the peak of the Rayleigh PDF is much higher than the mean. If the analyzer reports the peak of the signal, it is likely that the reported emission will be exaggerated, leading to false failures.
The RMS or average detector averages the power of the signal envelope during the bucket interval. If the bucket duration is set long enough, it can provide significant averaging, and thus be an excellent detector for reducing the risk of reporting an above-limit emission which is actually within limits. This detector is not as good for CW-like signals as a peak detector, because the spacing of the buckets must be made narrow compared to the RBW in order to reduce the errors that occur from not averaging only at the peak frequency of the signal. These errors are typically called "scalloping errors." The combination of a need for buckets of long duration for averaging and narrow width in frequency (thus, large numbers in a given span) can make for very long measurement times.
In this report, three major error sources will be considered as impacting spectral emissions measurements. One is the variance of the measurement of noise-like emissions. The second is the "scalloping error" from using a detector other than a peak detector to measure CW-like signals. The third is the sweep rate issue discussed previously.
When the noise-like signals are being measured, the measurement distribution is close to Gaussian. The standard deviation of this Gaussian distribution depends on the amount of filtering (VBW filtering) or averaging (average detector bucket duration). Consider the PDF in the middle section (for log averaging) of Fig. 2. This shape looks close to Gaussian. If the RMS deviation of this curve is computed from its mean, the PDF can be modeled as a Gaussian distribution with a standard deviation of 5.57 dB. If N independent samples of this noise are averaged on a log scale, the standard deviation would be 5.57 dB/(N)0.5.
However, averaging is not performed on a log scale, but on a power scale. Even though the PDF at the bottom of Fig. 2 does not look the least bit Gaussian, if it is averaged long enough, it will approach a Gaussian form, as expected from the central limit theorem. The standard deviation of the result is better than that of log averaging, when expressed in decibels: It is 4.35 dB/(N)0.5.
Page Title
Consider what happens when averaging with a VBW filter instead of averaging independent samples. The noisiness of the result depends on the amount of averaging, and that depends on the ratio of the spectral width of the video signal before filtering to the width after filtering. The spectral width before VBW filtering is one-half the noise bandwidth of the RBW filter, because converting the bandpass RBW output into a lowpass video signal halves its bandwidth. The noise bandwidth of the filters is 1.056 times the RBW. So the spectral width is one-half times 1.056 times RBW for near-Gaussian RBW filters. The VBW filter is a single-pole filter. The noise bandwidth of a single-pole filter is p/2 times its -3-dB width, thus p/2 times VBW. To compute the predicted standard deviation for a VBW-filtered noise signal, start with the 4.35-dB standard deviation of a power-scale noise signal, and divide it by the square root of the bandwidth-reduction ratio. The bandwidth-reduction ratio is the ratio of the RBW-controlled spectral width to the VBW-controlled post-filtered noise bandwidth. The result is a predicted standard deviation, as shown by Eq. 1:
σVBW = (7.50 dB)(VBW/RBW)0.5 (1)
Next, consider the case of variance reduction achieved by using an RMS detector instead of a VBW filter. It can be shown that the standard deviation is computed by Eq. 2, where tau is the duration of the bucket, and RBW uses a near-Gaussian alignment:
σPWR = (4.06 dB)/0.5 (2)
The amplitude of a CW signal is displayed to full accuracy with the peak detector, but is subject to what is sometimes called "scalloping error" when using other detectors. Figure 4 shows a video signal (see Fig. 1 for its location within the block diagram) with four different relationships between the time of the peak of the video signal and the time of the samples. Signal 1 reaches its peak exactly at the sample instant. In this case, the largest sampled amplitude is the same one that would be read by a peak detector. But as the signal moves to the right (signals 2 and 3), the highest bucket result becomes lower in amplitude. The worst case of the enumerated relationships is signal 3, with its peak close to midway between samples. As the signal moves further to the right, the highest bucket result correspondingly moves to the next bucket and starts to rise in amplitude.
Figure 5 is a graph of the highest sample amplitude versus the signal frequency. It repeats with a period of the frequency width of a bucket and has a scallop shape. Scalloping error is the difference between the highest sample result and the peak result. With a peak detector, the detector always reports the peak of the signal in the bucket, so scalloping error does not occur.
The RBW filters in modern analyzers are very close to Gaussian. Those in older analyzers are close enough to Gaussian to make for a useful approximation. Gaussian shapes in both the time domain and frequency domain are of the form exp(-x2). When expressed on a logarithmic (decibel) scale, they are of the form -x2, thus inverted parabolas.
Page Title
By definition, the response of the RBW filter is -3 dB at its one-RBW width points. The scalloping error will be 3 dB maximum when the bucket spacing is equal to the RBW, and will behave parabolically with bucket width as shown in Eq. 3:
ScallopErrorMaxSampleDet =
(3 dB)(BucketWidth/RBW)2(3)
When the average detector is used, it averages the signal amplitude across a bucket. The result still approaches a 0-dB error when the bucket width approaches zero, but the minimum error for finite bucket widths is not zero. It can be shown that the scalloping error varies between 1/3 and 4/3 of that for the average detector. The maximum error, then, for the average detector is shown by Eq. 4:
ScallopErrorMaxAvgDet =
(4 dB)(BucketWidth/RBW)2(4)
To evaluate two different spectral emissions measurement approaches, a search for unwanted 3GPP Long Term Evolution (LTE) cellular base-station operating-band emissions can serve as an example. Measurements will be made between 5.05 and 10.05 MHz offset from the edge of the carrier channel with a 100-kHz RBW. The goal is to maintain errors due to the measurement algorithm than to 0.2 dB.
Consider first the RMS-scale VBW filter technique that can be used with certain analyzers that have an "average type" or "avg&VBW" type keys that control the averaging scale for their VBW filters. This technique is subject to variance errors and sweep rate errors; because it uses a peak detector, it is not subject to scalloping errors. The spectrum of interest is swept using a narrow VBW filter working on the power scale (to achieve "RMS detection"), with a peak detector (to remove any scalloping error).
The goal of limiting errors at any frequency to 0.2 dB or less can be interpreted as a "3-sigma" goal. Thus, the standard deviation must be established as one-third of that value, or 0.067 dB, which will yield an error within the goal with 99.7% probability. Referring to Eq. 1, this implies that the VBW should be set to 7.9 Hz. The analyzer can be set to 7.5 Hz, the largest available bandwidth that is narrower. The analyzer automatically switches to a sweep time to minimize sweep rate errors (autocoupled sweep time); that sweep time for this span/RBW/VBW combination is 5.2 s.
The second technique to consider, the RMS detector technique, is subject to scalloping errors and variance errors. It is also subject to sweep rate errors, but these are small compared to the variance errors at all sweep rates and can be neglected. In using this approach for the LTE example, the RBW is set to the required 100 kHz and the VBW is set wide as a matter of good practice. To keep the scalloping error below the 0.2-dB goal, the width of each measurement point (also known as "pixel" or "bucket") must be kept below 0.224 times the RBW, or thus 22.4 kHz (Eq. 4). In analyzers with a continuously settable number of points in a sweep, the 5-MHz range can be covered with 224 points. To keep the variance down, the standard deviation of the measurement should again be 0.067 dB. This requires 37 ms (Eq. 2) per point sweep time, or 8.3 s total.
Page Title
The speed advantage of the RMS-scale VBW filter technique declines with increasing allowed errors, reaching parity at about a 0.45-dB error level. Figure 6 shows the relationship. When optimizing for speed and accepting an error rate greater than 0.45 dB, the RMS detector method should be used.
This comparison is sometimes unfair to the VBW method. It is fair in the case where the two methods are both being used to measure noise-like interferers. When measuring CW interferers, there are no additional errors for the RMS-scale VBW method, while the RMS detector method has a maximum error shown in the graph. If the RMS detector method were set up to keep the RMS errors the same for CW-like and noise-like interferers, instead of being set up so that the 3σ level for noise is equal to the worst-case level for CW errors, the RMS detector method would be slower than shown in the graph by 16%, and the VBW technique would be the faster one for error budgets up to 3σ = 0.6 dB.
In actual emissions measurements, the errors due to scalloping and variance can usually only be made simultaneously very small through the use of very long measurements. Therefore, a technique that would allow the identification of potentially out-of-tolerance emissions with a faster first-pass look and a closer study of candidate emissions with a second pass is desirable. This technique was suggested by Darcy Poulin of Microsemi Corp. Also, the use of RMS-based video filtering is not possible in many analyzers. Even though that technique has advantages in speed, we will also describe a technique that can make the measurement without the use of that unique capability.
The ITU-R SM.329 standard will be used in describing the measurement techniques, with requirements to measure spurious emissions between 30 and 1000 MHz with a 100 kHz RBW. For first-pass measurements, testing will allow for larger errors than the final goal. The ideal error budget for the first pass depends on the density of close-to-the-limit spectral components in the DUT. There is no ideal point for this, but 5 dB will be used in this example.
To keep the scalloping error below 5 dB requires that the width of each measurement point be kept to 1.12 times the RBW (Eq. 4), thus 112 kHz for this case. For a span of 970 MHz, this would require 8676 points. To keep the 3s performance within 5 dB requires a standard deviation of 1.67 dB, which requires that the measurement point have duration of 59 s (Eq. 2). The total sweep time would be 0.51 s.
For the second-pass measurements for out-of-tolerance emissions, slower sweep rates and narrow spans would be used. For example, with an analyzer having 0.1%-of-span (970 kHz) accuracy of its frequency readout, and an additional error from the limited (8676) points count, the sweep would go through 2.05 MHz to look for each candidate emission. To do this with the aforementioned RMS-scale VBW filter technique to a 0.2-dB level would require 2.1 s; with the RMS detector technique, it would require 3.4 s. By comparison, a 970-MHz single-pass sweep to the 0.2-dB level would require over 1000 s.
In summary, the two detection/averaging techniques for spectral emissions that have been reviewed here work for measurements where the emissions can be CW or noise like but still be measured to tight tolerances. Both techniques allow the use of single- and dual-pass approaches. The user can choose the measure-ment technique and single-/dual-pass approach in order to trade off measurement time while keeping three kinds of errors under control: variance, scalloping errors, and sweep rate errors.
References
1. Agilent Spectrum Analysis Measurements and Noise, Application Note 1303, Agilent literature number 5966-4008E, Agilent Technologies, www.agilent.com.
2. Agilent Spectrum Analysis Basics, Application Note 150, Agilent literature number 5952-0292, Agilent Technologies, www.agilent.com.
3. Joe Gorin, "Detector Selection for Spectrum Analyzer Measurements," RF Design, February 2003, pp 32-38, www.rfdesign.com.
4. Ben Zarlingo, "Signal Analyzer Detectors and Averaging for Today's Digital Communications Standards," Agilent Technologies,
http://www.agilent.com/cm/wireless/pdf/detector_averaging.pdf.
5. Spectrum Analysis (AN 63), Appendix B, Agilent literature number 5989-6251EN, July 1964, Agilent Technologies, www.agilent.com.