Optimize Settings For Improved Analyzer Sensitivity
Spectrum analyzers are often used to measure low-level signals. They may be known signals that must be characterized or unknown signals that must be found. In either case, knowing how to enhance the sensitivity of a spectrum analyzer can greatly aid the process. Certain spectrum-analyzer settings are optimum for measuring low-level signals, and these will be reviewed, along with how to use noise corrections and noise floor extensions to maximize a spectrum analyzer’s sensitivity.
A spectrum analyzer’s sensitivity can be found in the listing of specifications for a given instrument, usually as the parameter displayed average noise level (DANL) or as noise figure (NF). The DANL specification is the amplitude of the noise floor of the spectrum analyzer over a given frequency range with the input terminated in a 50-Ω load and with 0-dB input attenuation. The specification is normally given in units of dBm/Hz. In most cases, any averaging is performed on a logarithmic scale. Averaging causes a reduction in the noise floor by 2.51 dB. This reduction essentially differentiates DANL from NF. For example, for a -151 dBm/Hz DANL specification in a 1-Hz resolution bandwidth (RBW), it should be possible to lower the analyzer’s noise floor to at least this level using the settings provided in the specification. It should be noted that a continuous-wave (CW) signal with the same amplitude as the analyzer’s noise floor will measure 2.1 dB above the noise floor due to the summation of the noise and the CW signal. Similarly, a noise-like signal will appear 3 dB above the noise floor.
A spectrum analyzer’s noise floor has two components: the noise figure, denoted NFSA, and the thermal noise energy. The amplitude of the thermal noise energy is given by the product of three parameters, kTB, where:
k = Boltmann’s constant (1.38 x 10-23 J/°K;
T = temperature (in degrees Kelvin); and
B = bandwidth in which the noise is measured (in Hz).
This is the amount of thermal noise energy present at the input of the spectrum analyzer when the input port is terminated in a 50-Ω load. In most cases, the bandwidth is normalized to a 1-Hz bandwidth and, at room temperature, 10log(kTB) is calculated as -174 dBm/Hz. The DANL specification in a 1-Hz RBW is then given by:
DANL = -174 dBm/Hz + NFSA - 2.51 dB (1)
where:
NFSA = DANL + 174 dBm/Hz + 2.51 (2)
[Note: for cases where root-mean-square (RMS) averaging is used in the DANL specification, the 2.51 dB can be omitted from the calculations.]
For example, a -151 dBm/Hz DANL specification equates to a NFSA value of 25.5 dB.
Settings That Affect Sensitivity
A properly calibrated spectrum analyzer, where the display accurately reflects what is being applied at the input port, will exhibit unity gain, showing signals at their actual amplitudes. If a 0-dBm signal is applied to the input port, the measured/displayed signal should be 0 dBm plus or minus the accuracy of the analyzer. Adding attenuation or gain to the spectrum analyzer will change this relationship. Increasing input attenuation causes the spectrum analyzer to increase equivalent gain in the instrument’s intermediate-frequency (IF) stage to maintain a calibrated level on the display. This in turn raises the noise floor by an equivalent amount on the display, thereby maintaining the same signal-to-noise ratio. This applies to external attenuation as well. In the calculations, an RBW greater than 1 Hz is compensated by adding 10log(RBW/1 Hz). Through simple calculations (Eq. 3), it is possible to determine the spectrum analyzer noise floor at different settings of attenuation and RBW:
Noise Floor = DANL + Atten + 10log(RBW) (3)
An internal or external preamplifier can be used to improve the noise floor of a spectrum analyzer. Typically, there will be a second DANL specification that covers the internal preamplifier case and the previous equations will apply as well. If an external preamplifier is used, the new DANL can be found by using the cascaded noise-figure equations, with unity gain for the spectrum analyzer. Considering the system as the combination of a preamplifier and a spectrum analyzer, it can be represented by Eq. 4:
NFSYS = NFPREAMP + [(NFSA - 1)/(GPREAMP)] (4)
Using the previous example with NFSA = 25.5 dB and a preamplifier with gain of 20 dB and noise figure of 5 dB, the overall noise figure for this system of analyzer and amplifier can be found. The values must be first converted to power ratios and those results recorded:
NFSYS = 10log[3.16 + (355/100)] = 8.27 dB (5)
Equation 1 can then be used to determine the new DANL with an external preamplifier connected by simply replacing NFSA with the NFSYS calculated using Eq. 5. The preamplifier reduced the DANL significantly in the example, from -151 dBm/Hz to -168 dBm/Hz. The external preamplifier brings tradeoffs, however. Preamplifiers bring their own nonlinear distortion behavior to the system which can limit the capability to measure large signals. This is where an internal preamplifier is more useful because it can be simply switched in and out as the measurement needs change. This is especially true in an automated test environment.
So far, the sensitivity of a spectrum analyzer has been improved by modifications to the RBW, attenuation, and preamplifier gain/noise. Most modern spectrum analyzers offer methods for measuring the noise floor of the spectrum analyzer and then correcting for this in the measurement results—methods which have been available for some time.
Making Corrections For Noise
When a device under test (DUT) is measured with a spectrum analyzer, the resulting spectrum shown on the analyzer’s screen is actually a combination of the DUT’s input signal, the kTB noise, and the spectrum analyzer’s noise figure, NFSA. If the DUT’s input signal was disconnected, and the analyzer’s input port terminated in 50 Ω, the new spectrum would then be the combination of kTB and NFSA, or a trace on the screen of the spectrum analyzer’s noise floor.
Noise correction is a process by which the noise floor of the spectrum analyzer is measured, with the help of considerable averaging, and the noise floor trace is stored to a file called the Correction Trace. The DUT input signal is then connected to the spectrum analyzer and measured, with the results saved into a file called the Measurement Trace. Correction is applied when the Correction Trace is subtracted from the Measurement Trace and the results displayed in the Resultant Trace. The Resultant Trace is the spectrum of the DUT input signal with the excess noise removed, as shown by Eq. 6:
Resultant Trace = Measured Trace - Correction Trace = (DUT Input Signal + kTB + NFSA) - (kTB + NFSA) = DUT Input Signal (6)
It should be noted that all values are converted from dBm (logarithmic) to mW (linear) before subtraction is performed, although the resulting trace is displayed in dBm. This process makes it easier to view low-level signals as well as make more accurate amplitude measurements, since errors from the contribution of the spectrum analyzer noise floor have been removed.
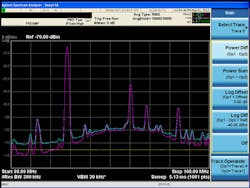
Figure 1 shows a relatively easy method for performing noise corrections with trace math. The noise floor of the spectrum analyzer is first averaged with the input terminated, with these results saved to trace 1. Then the DUT is connected and its signal captured and saved to trace 2. Trace math is then used for a power subtraction of the two traces, with the results saved to trace 3. The noise correction shows the most benefit when the input signal is close to the noise floor of the spectrum analyzer. Corrections have little or no effect on larger signals, which have a much lower contribution to noise.
1. These noise corrections were performed with the help of trace math.
The main issue with this approach is that the DUT must be disconnected and a 50-Ω load connected whenever a setting is changed. A method for measuring the Correction Trace without removing the DUT is to increase the input attenuation (say to 70 dB) to raise the spectrum analyzer noise floor far above the DUT input signal and then save this to the Correction Trace. The Correction Trace will now contain the components shown in Eq. 7:
Correction Trace = DUT Input Signal + kTB + NFSA + Atten (7)
If kTB + NFSA + Atten >> DUT Input Signal, it is possible to omit the DUT input level and state the Correction Trace according to Eq. 8:
Correction Trace = kTB + NFSA + Atten (8)
By subtracting the known attenuation from Eq. 8, it is possible to get back the original Correction Trace used in the manual method:
Correction Trace = kTB + NFSA (9)
The issue with this process is that the Correction Trace is valid only for the current settings of the spectrum analyzer. Changing settings such as center frequency, span, and RBW will invalidate the values stored in the Correction Trace. A better approach is to know the specific NFSA at all frequency points and then apply the Correction Trace for any setting.
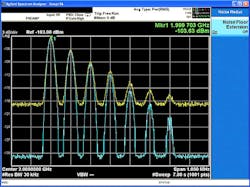
The N9030A PXA signal analyzer from Agilent Technologies is calibrated during manufacturing to better understand its noise behavior, as part of its Noise Floor Extension feature (NFE; Fig. 2). At the time of manufacturing and calibration, the analyzer’s noise figure is measured across the entire frequency range of the instrument. This data is then stored within the memory of the instrument. When a user turns on the NFE feature on the analyzer, the analyzer calculates a Correction Trace based on the current setting of the instrument and the stored noise figure values. This eliminates any need for measuring the noise floor of the PXA, as was done in the manual procedure. This greatly simplifies the use of noise corrections and eliminates the excess time needed for measuring the noise floor of the instrument whenever a setting has changed.
2. The Noise Floor Extension (NFE) feature in the Agilent N9030A PXA signal analyzer helps improve low-level signal sensitivity.
Conclusions And Resources
In these different methods, the thermal noise, kTB, is subtracted from the measured trace as well as the NFSA so that results below kTB can be displayed. These results can be valid in many, but not all, cases. Problems occur when the measured values are close or equal to the noise floor of the instrument. In fact, if they are equal, the result would be -infinity dB. Practical implementations of noise corrections normally includes a threshold or a graduated level of subtraction close to the noise floor of the instrument.
This report has examined some of the techniques for measuring low-level signals with a spectrum analyzer. It has pointed out that sensitivity is affected by RBW, attenuation, and use of a preamplifier. Noise reduction methods, such as noise corrections and noise floor extension, can be applied to further enhance the sensitivity of the instrument. In practice, ensuring that external path losses to the spectrum analyzer are reduced can aid tremendously.
Additional Information
More information about spectrum analyzer measurements and analysis can be found in the following application notes:
Agilent Spectrum and Signal Analyzer Measurements and Noise, Application Note 1303.
About the Author
Bob Nelson
MXA (N9020A) Product Support Engineer
Bob Nelson is Agilent Technologies’ MXA (N9020A) Product Support Engineer. He has spent the last 14 years with the company, supporting the Agilent field organization and customers with application-focused measurement requirements. Nelson holds a degree in Electrical and Electronic Engineering from California State University, Chico.