Optimize Spectrum-Analyzer Settings For TOI Measurements
One of the more common measurements made with an RF/microwave spectrum analyzer is determination of third-order-intercept (TOI) point for a device under test (DUT), which is often an amplifier. TOI point is a parameter used to evaluate the linearity of components that are utilized in applications where nonlinear effects can cause distortion—for example, in digitally modulated signals. This measurement can be challenging, as uncertainties vary significantly based on the spectrum analyzer’s settings. To optimize these settings using traditional, manual measurement techniques, the engineer often has to make difficult tradeoffs between dynamic range, measurement time, repeatability, and uncertainties. Is there a better way? Let’s take a closer look.
Manual Measurement Optimization
The TOI measurement is made by combining two fundamental tones at frequencies ω1 and ω2 and measuring the relative level of the two third-order distortion products at frequencies 2ω1 - ω2 and 2ω2 - ω1. As the amplitude of the fundamentals is increased by 1 dB, the absolute level of the third-order distortion products increases by 3 dB. For the same 1-dB increase to the fundamental amplitude, the relative (dBc) change of the distortion products increases by 2 dB (Fig. 1).
1. Shown are both fundamental and distortion products.
By measuring a single relative-distortion level for a given DUT output level, it is possible to calculate the theoretical level at which the distortion products are equal to the fundamental. This is the TOI point. Mathematically, this is given by:
TOI = Afund – d/2 Equation 1
where Afund = the level of the fundamental in dBm and d = the difference in dB between fundamental and distortion.
In addition, the line can be plotted with a slope of 2, representing the relative distortion based on the DUT output level. Figure 2 shows an example of a TOI plot for a DUT with –64-dBc distortion products relative to a fundamental output level of –10 dBm. It yields a DUT TOI of +22 dBm.
2. This dynamic-range plot yields a DUT third-order intercept of +22 dBm.
The spectrum analyzer also produces internally generated, third-order distortion products at exactly the same frequencies as those generated by the DUT. These distortion products are relative to the mixer level, rather than the output level of the DUT. This distinction enables the measurement of a DUT with a significantly higher TOI than that of the spectrum analyzer. An example plot of the relative distortion-to-mixer level for a spectrum analyzer with a TOI of +15 dBm is shown in Figure 2.
The mixer level, which is given by Equation 2, can be set by increasing or decreasing the input attenuation in the spectrum analyzer. Ideally, the internally generated distortion products should be much less than those generated by the DUT. If the internally generated distortion products are equal to the DUT distortion products, for example, the uncertainty is between +6 dB and –infinity (based on the phase relationship of the two signals). The optimum mixer level is the level at which the spectrum analyzer’s internally generated distortion products are equal to its noise floor for a given resolution bandwidth (RBW). A plot of the mixer level versus displayed average noise level (at 1 kHz RBW) shows the signal-to-noise-ratio (SNR) improvement as the mixer level is increased. In this example, a –30-dBm mixer level provides a –90-dB SNR.
Mixer level = Input level – External attenuation – Input attenuation Equation 2
A DUT output level of –10 dBm with 20-dB attenuation provides a mixer level of –30 dBm (as shown in Figure 2). The TOI plot for the spectrum analyzer shows that the internally generated distortion products are –90 dBc relative to this mixer level. This allows for a 26-dB margin between the DUT and internally generated distortion products. If additional dynamic range is needed, the mixer level will need to be reduced by increasing the attenuation. The RBW also will need to be decreased to compensate for the spectrum analyzer’s increased noise floor. Reducing the RBW adversely effects measurement time, as given by:
Sweep time = K*SPAN/RBW2 Equation 3
or
Sweep time = K*SPAN/(RBW*VBW) for VBW < RBW Equation 4
where K is a constant that is unique to the spectrum-analyzer model and settings.
In practice, the best approach is to increase the internal attenuation until the displayed distortion products no longer change in amplitude. At that point, the internally generated distortion no longer contributes to the results.
The variance in measurement results is primarily caused by a low SNR of the distortion products to the spectrum analyzer’s noise floor. Measurement repeatability can be improved by narrowing the RBW and/or applying averaging. Normally, such variance can be reduced through trace averaging or by reducing the video bandwidth (VBW) to a value less than the RBW. Log-video averaging is another option. It causes an under-respond to the noise trace, thereby improving the SNR of the distortion products.
Regardless of the method employed, additional measurement time will be needed. Spectrum and signal analyzers that are capable of noise-floor extensions (NFEs), such as Agilent’s N9030A PXA, use this capability—along with root-mean-square (RMS) power averaging—to achieve optimal variance with respect to measurement time.
An Alternative Approach
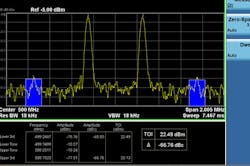
An automated, one-button TOI measurement (like that available in Agilent’s X-Series signal analyzers) allows the user to quickly set up the measurement for optimum accuracy and dynamic range—without many of the tradeoffs associated with the traditional manual-optimization method. With this measurement, the user automatically sets the center frequency and span by pressing the Auto Tune soft key. The optimum attenuation level is then quickly set by pressing the Adjust Attenuation for Minimum Clip key. Next, the two fundamental signals are measured and the relative level (dBc) of the distortion products is measured and displayed. Finally, TOI results are calculated and displayed (Fig. 3).
A zero-span measurement method allows the user to make high-dynamic-range measurements while optimizing for measurement speed. The measurement sweeps the entire trace in a wide RBW and measures the amplitude level of the two fundamental signals. The instrument then measures the two distortion products in a user-selectable narrow RBW. The distortion products are measured in zero span in a user-defined dwell time. Raising this dwell time increases the number of samples that are averaged, improving the variance.
3. With an automated, one-button TOI measurement, the user can quickly set up the measurement for optimum accuracy and dynamic range.
The measurement-time tradeoff of traditional averaging methods is much more severe than the zero-span method. This is because the sweep time between products, which is wasted time, increases square-law operation by reducing the RBW.
Summary
Traditionally, TOI measurements have been optimized using manual techniques. Yet this same task can now be accomplished with an automated, one-button, TOI-measurement solution and optimization techniques. For the user, the benefits of such an approach are clear: faster, better-optimized TOI measurements without many of the unfavorable tradeoffs associated with the more traditional measurement approach.
Bob Nelson is Agilent Technologies’ MXA (N9020A) Product Support Engineer. He has spent the last 14 years with the company, supporting the Agilent field organization and customers with application-focused measurement requirements. Nelson holds a degree in Electrical and Electronic Engineering from California State University, Chico.
About the Author
Bob Nelson
MXA (N9020A) Product Support Engineer
Bob Nelson is Agilent Technologies’ MXA (N9020A) Product Support Engineer. He has spent the last 14 years with the company, supporting the Agilent field organization and customers with application-focused measurement requirements. Nelson holds a degree in Electrical and Electronic Engineering from California State University, Chico.