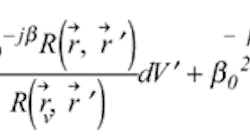Long-term effects of electromagnetic (EM) radiation from cellular and Personal Communications Services (PCS) handsets are still unknown. Prudent practices include the use of measurement tools to detect unusually high levels of EM radiation from, for example, broken gaskets in a cellular handset package. Another safety measure is to measure the radiation levels from wireless handsets using a low-cost radiation checker as proposed in this article. This report will present the design, review its principles of operation, and demonstrate its effectiveness in measuring cellular-handset radiation.
The radiation checker consists of an antenna (two identical elements), a plane small reflector, a detector including a matching circuit, a moving-magnet meter, and a plastic cover. The antenna is placed about one-tenth of a wavelength away from the reflector to receive maximum energy from EM radiation source. The received radiated energy by the antenna passes through a detector and a matching circuit to provide appropriate current for the movement of the magnet. The deflection of moving magnet is proportional to the received current. A substitution method has been used to verify the calibration of the radiation checker in mW/cm2.
The biological effects of UHF and microwave frequencies have been a concern for years. Recently, Lai et al.1-3 and Phillips et al.4 have reported that the EM radiation emitted from a cellular/PCS phone is dangerous for animal/human cells. Their results show that there is DNA damage in rats due to electromagnetic radiation below l mW/cm2. Another group of scientists 5-8 have reported that the EM radiation did not increase the number of single-strand DNA breaks in rats. Recently, Kumar9 provided a review on the biological effects of low power radiation on human and animals and why groups differ on DNA damage.
There are many large and expensive commercial radiation monitors. This new radiation checker should not be confused with those larger radiation monitors. A radiation checker is used for a quick read of EM radiation and not for precision measurements of EM radiation. Still, the radiation checker does provide full-scale sensitivity of 0.001mW/cm2 for detection of low-level radiation.
The radiation checker measures the total EM radiation incident on the human head in the near-field. Kumar 10,11 and Chung12 have reported that, due to body absorption effect, only about 29 to 72 percent of the antenna input power is radiated into free space for various-head distances (1 to 5 cm). The closer the distance, the less the antenna input power is radiated into free space. Thus, strong EM coupling at close distances increases the body absorption effect. It has also been reported that the head absorbs more than 80 percent of the whole-body absorbed power since the antenna is located in front of the head. Since it is compact, a radiation checker can provide a good indication of absorbed power into the head.
The radiation checker's antenna works on the principle of the cavity resonator.13 One end of the dipole is connected to the structure's positive terminal and other end is connected to the negative terminal (Fig. 1). Figure 2 shows a simplified version of a backfire antenna model, which consists of a large reflector,13 a small reflector, and a dipole antenna. The large and the small reflectors are parallel to each other, at a distance c. The planes of both reflectors are transverse to the longitudinal axis. The dipole radiator is placed closed to the small reflector. The dipole antenna is placed at a distance d from the small reflector. According to the diagram of Fig. 1, two surface-wave-modulated structures lie between the two reflectors. The first is connected to the positive end and the second to the negative end, with a diode connected between the positive and negative terminals.
When an EM wave is incident upon the large reflector, it travels directly from the large reflector to the small reflector, through the modulated-surface-wave structure, and a resonant cavity is formed. The dipole structure picks up the EM wave, which passes through a diode detector. The diode detector converts the alternating-current (AC) EM wave to direct current (DC), which passes through the positive and negative ends of the dipole to the coil. The coil and magnet are placed in the back of the large reflector. There are no electrical contacts between the large reflector and the modulated-surface-wave structure.
In Figure 2, the center of the large reflector is placed at the origin of a Cartesian coordinate system with its y-axis lying along the cavity antenna axis. The dipole primary radiator is parallel to the z-axis with half-length h and radius a, and its center is located at y = d along the positive y-axis. The small reflector is parallel to the x-z plane with its center along the positive and negative y-axis at y = c.
Integral equations for the induced current excited in the dipole and on the surface of the small reflector were formulated based on the boundary condition that the tangential electric field vanishes at all conducting surfaces. In calculating the received radiation field on the antenna, the large reflector currents are truncated by using the actual size of the reflector. Image techniques determine the currents induced in the primary dipole antenna and on the surface of the small reflector.
The radiated field emitted by the source is captured by the combination of the plane reflector (λ/6) and the curve surface (λ/8). The extension of the curve surface supports the assumption that the large reflector is infinite in extent in theoretical calculations of the E-field. The EM field E(r) at any point in space, maintained by all the currents in the antenna system is:
where:
βo = 2π/λo, the free-space wave number,
ξo = (εo /µo)1/2, the free-space wave number,
R(r, r′) = |r –r′| is the distance between the field point at r and a source point at r′, and
V = the volume including all the currents in the antenna system.
The term J(r′)dV′, in this case, consists of the current z Iz(z′)dz′ in the dipole, the surface current Kr(r′)ds′ = rx (x′, z′) + xKrz (x′, z′)>ds′ on the small reflector as well as the effects of their images. Currents xIz and Kr are imaged into the y = 0 plane to replace the effects of K′s on the large reflector and concurrently satisfy the boundaries conditions at its surface. The surface current is excited on the conducting plane, which is determined from the electromagnetic field maintained by the currents in the dipole and on the small reflector, and their images (Figs. 2 and 3). The large reflector has diameter of 6 cm while the small reflector has diameter of 1.8 cm, with 3.5-cm distance between the two.
Page Title
In order to determine the induced current numerically, the dipole is partitioned into a number of subsections, and the small reflector is partitioned into a number of rectangular subareas. Within the subsections or subareas, the induced current is assumed to be approximately constant, and equal to its value at the center of the partition. In order to calculate the received radiation field in terms of the various current distributions, the dipole is again partitioned into a number of subsections, and the two reflectors are partitioned into a number of rectangular subareas. The induced current is assumed approximately constant over each partition, and equal to its value at the center partition. Figure 3 shows the geometry for the received radiation field calculation. The EM radiated field received by the large reflector of the antenna system is given by:
The EM radiated field received by the small reflector of the antenna system is given by:
The EM direct radiated field received by the dipole antenna from the external source is calculated by:
The total EM radiated field maintained the antenna system (the large reflector, the small reflector, and the dipole) is the superposition of the EM fields described by Eqs. 2, 3, and 4, and it is expressed as:
The total received EM field of Eq. 5 is radiated in the vertical-plane polarization and passes through the diode in the detecting circuit. The detecting circuit converts AC to DC. The DC is given by:
i = k1 k2E (6)
where:
E = |Er (r, θ, φ)|,
k1 = the radiation field constant, and
k2 = the detector circuit constant.
DC flows from the positive (+Ve) to the negative (–Ve) end of the circuit, which passes through a coil in the back of the large reflector. The coil of thin wire is wrapped on a plastic frame and two moving magnet wheels pass through the coil frame. One end of the magnetic wheel is connected to a needle and the other end is connected to a frictionless bearing.
Due to DC in the coil, a torque (T) is generated on the axis of the magnetic wheel. The torque is proportional to the DC(i), flux (φ), number of turns (n) in the coil, and the size of the coil (A):
T ∝ (i,φ, n, A) (7)
In Eq. 7, n , φ , and A are constant as denoted by k. Equation 7 can be rewritten as
T = ki (8)
Deflection of the needle on the dial is proportional to the torque, which is calculated from Eq. 8. The dial of the radiation checker is calibrated to read mW/cm2, which is proportional to the torque, i.e.,
mW/cm2 ∝ T (9)
Figure 4 shows a photograph of the front view of the radiation checker with a plastic cover. Behind the transparent plastic cover (on the top), there is a deflection needle and a calibrated dial which can be seen from outside. In the bottom part of the front cover (behind the non-transparent part of the plastic cover), the checker contains a plastic frame with a coil. A magnetic wheel passes through the coil, which is connected to the needle. The plastic frame is fixed on a plastic hub with glue and a metal screw. The metal screw is connected to the large reflector (metallic body). One end of the coil is soldered to a positive stud, which is denoted as positive terminal rod and other end of the coil is soldered to a stud, which is called negative terminal of the radiation checker. When, the antenna of the checker is placed near the radiating EM field, it receives the radiation E-field. This E-field is detected and converted from AC to DC via the detecting circuit. The output of the detecting circuit generates an electric current, which is applied to the coil. The magnetic wheel moves according to the Ampere's law, which is calculated from Eq. 8. The movement of the magnetic wheel is read on the dial through a needle.
Figure 5 shows a plot of the radiation in mW/cm2 versus angle of rotation from Eq. 9 at UHF. The maximum value of radiation is 0.65 mW/cm2. Figure 6 shows a plot of the radiation versus angle of rotation at 1900 MHz. In both cases, the radiation checker is irradiated from its back in the right angle with the electric field vector parallel to the axis of the detector circuit (which is received in the vertical polarization). When the radiated electric field vector is perpendicular to the axis of the detector circuit, the electric current becomes very small/negligible in the coil and therefore, there is no deflection in the meter. Heavy dots denote measured values of the radiation. The maximum value of radiation is 1.1 mW/cm2.
Figure 7 shows measured values of radiation in the frequency range 800 to 920 MHz. The frequency response is flat from 820 to 900 MHz. Radiated power decreases from 0.65 to 0.35 in both lower (below 820 MHz) and higher (above 900 MHz) frequency ranges at UHF. The main reason for decrease in power is that the antenna bandwidth is very narrow. It is not possible to increase the bandwidth of the antenna in the frequency range of 800 to 1990 MHz and therefore, we have matched the antenna in two separate frequency bands: 1) 820 to 900 MHz and 2) 1850 to 1955 MHz. Figure 8 shows the frequency response of the radiated power picked up by the checker. Measured values of the radiation are shown by heavy dots in the figure. The radiated power is constant in the frequency range of 1850 to 1955 MHz. The return loss is below –10 dB in both frequency bands. Both frequency bands are matched by tuning the matching circuit separately. Since the antenna is narrowband, two separate units have been developed for the two frequency bands.
A radiation monitor from Narda Microwave (Hauppauge, NY) was used to calibrate the radiation checker by a substitution method. The radiation checker has been developed as a reliable, low-cost means of measuring the radiation emitted by cellular/PCS telephones. The checker operates without batteries, powered by the strength of radiated EM field that it is measuring (see table). An operator simply turns on the cellular/PCS phone, holds the radiation checker near the source under test, and moves the checker around the operating area for maximum deflection. The back of the radiation checker should face the expected source of radiation, and results will be shown in mW/cm 2.
REFERENCES
- H. Lai and N.P. Singh, "Acute low-intensity microwave exposure increases DNA single-strand breaks in rat brain cells," Bioelectromagnetics, Vol. 16, 1995, pp. 207-210.
- H. Lai and N.P. Singh, "Single-and double-strand DNA breaks in rat brain cells offer acute exposure to radiofrequency electromagnetic radiation," International Journal of Radiation Biology, Vol. 69, No. 4, 1996, pp. 513-521.
- H. Lai and N.P. Singh, "Melatonin and spin-trap compound block radiofrequency electromagnetic radiation-induced DNA strand breaks in rat brain cells," Bioelectromagnetics, Vol. 18, 1997, pp. 446-454.
- J.L. Phillips, O. Ivaschuk, T. Ishida-Jones, R.A. Jones, M.Campbell-Beachler, and W. Haggren, "DNA damage in Molt-4T-lymphoblastoid cells exposed to cellular telephone radiofrequency fields in vitro," Bioelectrochemistry and Bioenergetics, Vol. 45, pp. 103-110, 1998.
- R.S. Malyapa, E.W. Ahem, W.L. Straube, E.G. Moros, W.F. Pickard, and J.L. Roti-Roti, "Measurement of DNA damage after exposure to 2450 MHz Electromagnetic radiation," Radiation Research, Vol. 148, 1997, pp. 608-617.
- R. S. Malyapa, E.W. Ahem, W.L. Straube, E.G. Moros, W.F. Pickard, and J.L. Roti-Roti, "Measurement of DNA damage after exposure to electromagnetic radiation in the cellular phone communication frequency band (835.62 and 847.74 MHz)," Radiation Research, Vol. 148, 1997, pp. 618-627.
- N.P. Singh, R.E. Stephens, and E.L. Schneider, "Modifications of alkaline microgel electrophoresis for sensitive detection of DNA damage," International Journal of Radiation Biology, Vol. 66, 1994, pp. 23-28.
- P.L. Olive, D. Wlodek, R.E. Durand, and I.P. Banath, "Factors influencing DNA migration from individual cells subjected to gel electrophoresis," Experimental Cellular Research, Vol. 198, 1992, pp. 259-267.
- A. Kumar, "Electromagnetic radiation and biological effects," Proceedings of the 2001 IEEE EMC Symposium, Vol. 2, August 2001, pp.1048-1053.
- A. Kumar, "Microwave radiation, calculations and shielding," Proceedings of the Canadian Conference on Electrical and Computer Engineering, Montreal, Canada, September 1989, pp. 922-925.
- A. Kumar, "RF radiation and radiation checker for cellular phone," Proceedings of the Third Annual Wireless Symposium, Penton Media, February 1995, pp. 80-87.
- H.R. Chung, "Human operator coupling effects on radiation characteristics of a portable communication dipole antenna," IEEE Transactions on Antennas & Propagation, Vol. AP-41, pp. 556-560, 1994.
- A. Kumar and H.D. Hristov, Microwave cavity antennas, Artech House, Norwood, MA, 1989.