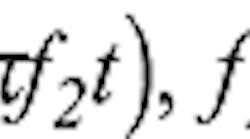This file type includes high resolution graphics and schematics when applicable.
Power meters are often considered for mobile-telephone production testing, because they can quickly measure peak power, average power, and peak-to-average ratio. But an RF power meter has certain deficiencies that hinder accurate wireless handset testing. For example, an RF power meter cannot identify where in the frequency spectrum a device is transmitting its power. Because of this, a handset may pass a power test with a power meter, but transmit at the wrong frequency or suffer excessive spurious transmissions. Fortunately, frequency-domain analysis performed on spectrum analyzers and RF power analyzers can overcome these limitations. An RF power analyzer provides both power and transmission frequency information, and can also overcome false readings associated with an RF power meters limited video bandwidth.
In production, every mobile telephone is checked for carrier frequency, primary-channel power, adjacent-channel power, and alternate-channel power. Typically, such instruments as RF power meters, spectrum analyzers, and RF power analyzers are used for such testing, but the capabilities of and results from these tools can vary widely. To maximize measurement throughput and accuracy, the trade-offs of these measurement instruments should be considered.
RF power meters are used not only for measuring power levels in two-way radio systems, broadcast systems, and radar/satellite systems, but for calibrating other measurement instruments and probes. Unfortunately, an RF power meter is designed for broadband frequency coverage and cannot determine the carrier frequency associated with a power reading or whether the measured power is within the proper bandwidth. Normally, a spectrum analyzer is also needed to make these determinations.
An RF power meter is basically an untuned RF sensor or detector followed by signal-processing circuitry consisting of DC or AC-DC amplification stages and analog-to-digital-conversion (ADC) stages (Fig. 1).
It is designed to measure RF power, including peak power, average power, and peak-to-average power ratio. It does not measure frequency, since all frequency information is lost before signal processing begins. While this is a drawback in some ways, no tuning is required for a measurement. If the input signal is anywhere in the frequency range of the detector, the meter will make a valid power measurement.
An RF power meter measures input signals in the time domain. An incoming carrier of constant amplitude will produce a DC output, while any amplitude variation will be reproduced in the output, as the instrument responds to the envelope of the incoming signal. Because of this, the instrument's video bandwidth is an important characteristic when peak detection measurements are required.
The video bandwidth of a test instrument, in simplest terms, is an indication of how fast it can track signal variations for peak power envelope measurement, and can be considered the range of frequencies occupied by all the modulating signals. For example, a wideband-code-division-multiple-access (WCDMA) signal consists of a 1950-MHz carrier modulated by a 3.84-MHz modulating signal; after detection, the signal that remains extends from 0 to 3.84 MHz. For an instrument to process that signal correctly, all circuits downstream of the detector must have a bandwidth greater than 3.84 MHz (and preferably 5 MHz). An instrument with a narrower bandwidth cannot follow or capture the peaks of the 3.84-MHz WCDMA signal envelope. Video bandwidth is not the frequency range over which the instrument itself can accept signals; it is an indication of how well the power meter can capture the peaks of a modulated waveform.
Time variations in the detected signal can come from several sources. The obvious source is pulse or amplitude modulation. For example, if the incoming signal is pulse-modulated at 1 MHz, the bandwidth of the circuits following the sensor/detector would have to be greater than 1 MHz to accurately measure the peak value, although average value measurement would still be accurate with a smaller video bandwidth.
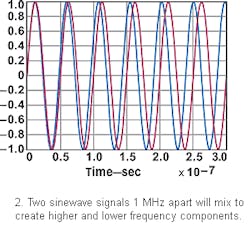
How video bandwidth affects peak power measurements and time-gated average power measurementsa but not average power is illustrated in the following example. Two RF sinewave signals (in the 800-MHz range) whose frequencies differ by 1 MHz and have magnitudes equal to one are represented in Fig. 2:
Assuming the impedance is 1 for the convenience of power calculations, the power versus time (real-time power) of these two signals is represented as Eq. 1:
Substituting v1 and v2 by their sinewave equivalents, power versus time, P(t), is derived in Eq. 2, which indicates that P(t) consists of the power of two individual signals (v1, v2) and twice the amplitude product of the two signals:
Equation 3 is inferred by applying trigonometric identitiesb into Eq. 2. Equivalently, P(t) consists of one DC signal and four frequency components, which are 2f1, 2f2, f1 + f2, and f1 − f2, respectively:
The average power is defined by and calculated from
which is the DC component of Eq. 3.
From Eqs. 3 and 4, the peak power depends on all components while the average power depends on the DC component only. If a power meter and power sensor has a 1-MHz video bandwidth, it will act as a typical low pass filter with a 3-dB rolloff point at 1 MHz. With regard to the power envelope, components 2f1, 2f2, f1 + f2 are filtered, leaving the DC offset and the |f1 − f2| = 1 MHz, periodic signal as seen in Eq. 3. If the video bandwidth is greater than 1 MHz, the peak value is 2. However, the |f1 − f2| term is attenuated in half (3 dB) due to the 3-dB rolloff at 1 MHz. This causes a 1.24-dB error for peak-to-average ratio.c Video bandwidth affects the measurement of the peak of the power envelope but has no effect on average power measurement.
This might lead to the impression that a wider video bandwidth is always preferable to a narrower one, but that is not the case. For one thing, the greater the instrument's video bandwidth, the smaller its dynamic range and the greater the variation in linearity. For example, a video bandwidth of 5 MHz will give a dynamic range of −32 to +20 dBm, while a 300-kHz bandwidth will give a dynamic range of −42 to +20 dBm.
Page Title
In general, the instrument's video bandwidth should be equal tod or greater than the input signal's modulation bandwidth. Table 1 lists recommended video bandwidths for different wireless standards. For example, a cdmaOne signal has a 1.23-MHz modulation bandwidth, and the recommended video bandwidth is 1.5 MHz. For multiple signal types, it may be necessary to consider multiple sensors.
An RF power meter has one major drawback: it cannot measure frequency, so it may give an "approved" rating to a defective mobile telephone, as in the following two examples.
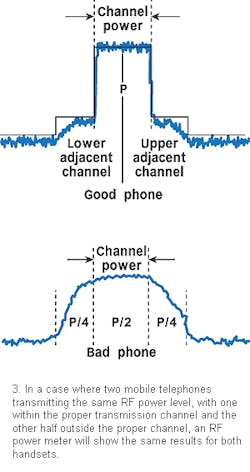
In the first example, two mobile phones are transmitting the same RF power, with the spectrums shown in Fig. 3.
The good telephone has its power within the transmission channel, while the output of the defective telephone is half in the transmission channel and half outside, probably because of a bad modulator or power amplifier. A power meter will give the same reading for both telephones.
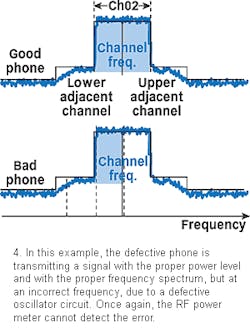
In the second example (Fig. 4), the defective phone is transmitting a signal with the proper power level and with the proper frequency spectrum but at an incorrect frequency, due to a defective oscillator circuit. Once again, the RF power meter cannot detect the error.
No matter where the RF signal is centered, the power meter reads the same total average power value (Table 2). The RF power analyzer is programmed to read the power only in the channel in which the mobile device is supposed to be transmitting. As the signal is shifted from the original center frequency, the RF power analyzer reads lower and lower power levels as more and more of the signal shifts out of the intended transmission channel.
Both an RF power analyzer and a spectrum analyzer are essentially specialized superheterodyne receivers. They have mixers, local oscillators, and IF chains. The essential difference is that the spectrum analyzer, being designed for laboratory use, is designed to cover an extremely wide frequency range with widely adjustable tuning range, bandwidth, etc. It uses one or more sweeping local oscillators (Fig. 5), while the RF power analyzer uses one or more fixed-frequency local oscillators (LOs), an analog-to-digital converter (ADC), and a digital signal processor (DSP) to extract information on the primary channel, the upper and lower adjacent channels, and the upper and lower alternate channels (Fig. 6).
Unlike a spectrum analyzer, an RF power analyzer is optimized for high-volume production testing and features a wide dynamic power measurement range. As a production test instrument, it is intended for one job: mobile-telephone testing during production.
The ability of the RF power analyzer to measure power within specified frequency bands enables it to spot defects that an RF power meter cannot. In Fig. 3, the RF power analyzer would give a reading one-half as great as that of the RF power meter, because it would measure only the power within the intended channel. In Fig. 4, the RF power analyzer would again give a reading one-half that of the RF power meter, because one-half of the transmitted power is outside the designated band. In addition, the RF power analyzer has a carrier-frequency-measurement function, and would immediately detect the off-frequency situation in Fig. 4.
A high-end spectrum analyzer can make the measurements of an RF power analyzer, with similar accuracy. Unfortunately, the spectrum analyzer costs more than the RF power analyzer (as much as $43,000 versus about $16,000 for an RF power analyzer). The spectrum analyzer is also more complicated to set up, is physically larger, and takes much more time to make a measurement. For development work, a spectrum analyzer is indispensable. But for production testing, it offers more measurement power (and expense) than needed.
When total RF power transmitted is the key parameter—in a two-way radio system or an antenna system, for example—an RF power meter is an excellent solution. But when information is also needed about the transmit frequency, as in mobile-telephone production testing, the RF power analyzer is a better choice.
FOOTNOTES
aAlthough time-gated average power is a type of average power measurement, it requires quick response from a power sensor. How fast the response will be is limited by the video bandwidth of a power sensor.
bNote that sinA · sinB = 0.5, with cos2A = 1 − 2sin2A implying that sin2A = (1 − cos2A)/2.
cThere is no attenuation at 1 MHz, since peak power = 10log(Ppeak/Paverage) = 2/1 = 3.0 dB. However, there is a 3-dB rolloff at 1 MHz, with peak power = log(Ppeak/Paverage) = 1.5/1 = 1.76 dB.
dThe video bandwidth of some power sensors is not the traditional 3-dB bandwidth.
This file type includes high resolution graphics and schematics when applicable.