Transmit jitter is not always the most effective method of predicting bit error rate (BER). For a more productive BER evaluation, timing and voltage variations can be used. Additionally, proper analysis of an eye diagram could provide detailed knowledge on how receive and transmit jitter affect the eye diagram. These factors can be analyzed using a statistical approach, which Mentor Graphics examines in the application note, “The Jitter-Noise Duality And Anatomy of an Eye Diagram.”
One method for capturing BER is to use normalized positive and negative eye-density branches, which can then be integrated in the vertical direction. The product of these probability densities can then be added to form a combined BER plot. This method may produce results that are only minimally affected by timing jitter and noise.
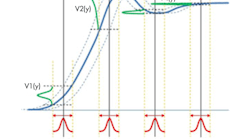
Another method is to horizontally integrate the eye-density branches. However, this approach may allow for errors when an eye is closed. It also may miss certain trajectories that are above or below the line of integration. As a result, horizontal integration may only be accurate in monotonic cases. As a product of the integration function, horizontal integration may provide less insight into channel behavior.
When considering jitter, the vertical probability density function (PDF) derived from the horizontal PDF could more accurately determine receive jitter. Using the vertical PDF over the convolution of a sample of step responses with the horizontal PDF lends robustness toward phase variation in the responses. While the horizontal convolution approach can still be used to find the slow, or correlated, portion of the transmit jitter power, the vertical PDF approach can be used to find the fast, or uncorrelated, portion. Another benefit of the vertical approach is the ability to derive the eye density from the vertical PDF added with the receive jitter.
The note covers generating the discrete PDF, or probability mass function (PMF), by fitting an arbitrary probability density into PMF using the mean value as the first moment. This process produces a PMF, which is a vertical cross-section of the eye density. Care must be taken with this approach to prevent an increased additional standard deviation value.
Mentor Graphics, 8005 SW Boeckman Rd., Wilsonville, OR 97070; (800) 547-3000