This file type includes high resolution graphics and schematics when applicable.
Direct-digital synthesis (DDS) is a mature digital-signal-processing (DSP) technology that offers great flexibility and power for generating complex waveforms. One of the advanced waveforms within the realm of DDS creation (given a dual-accumulator architecture) is chirp or linear frequency-modulation (FM) signals. In contrast to larger and more expensive arbitrary waveform generators, DDS chirp sources can save power, size, and cost in critical designs.
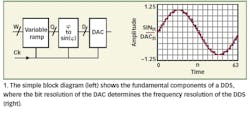
The principles of DDS technology were formulated in the late 1960s. In almost the reverse of sampling theory, a DDS source produces digital samples of a sinewave by means of an accumulator and sine lookup table; these digital samples are converted to analog waveforms via a digital-to-analog converter (DAC) and filter (Fig. 1, left) . The number of digital bits in the process determines the ultimate resolution of the output waveform (Fig. 1, right) .
A variable phase ramp is achieved by means of an accumulator with W digital bits. The accumulator is a phase generator in which 2W states represent 2π phase conditions. Of the accumulator's W bits, Q (most significant) of these bits ( usually Q
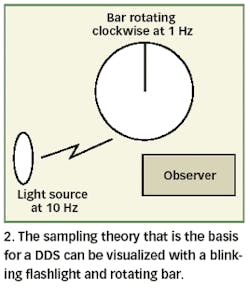
A simple example may serve to demonstrate the properties of the sampled data as well as the concept of positive and negative frequencies. In this example, a bar is rotating at a rate of 1 Hz and illuminated by a flashlight (sampled) blinking at a rate of 10 Hz (Fig. 2).
Each time the light flashes, the bar appears to rotate 36 deg. forward in a clockwise motion, although this interpretation is not conclusive. The bar can rotate at 1 Hz, or 11 Hz, or 21 Hz, or any frequency that is 10N + 1 Hz and be interpreted in a similar fashion under the strobe light. In addition, there is another set of infinite frequencies that are given by 10N - 1 Hz, rotating counter clockwise, that yield same results. Because they rotate counterclockwise, they are called negative frequencies, 180 deg. relative to the main set of frequencies. Generally, the set NFs + Ff or NFs- Ff (where Fs is the sampling frequency, Ff is the fundamental frequency, and N is the multiplication factor), generate the same sampled data response.
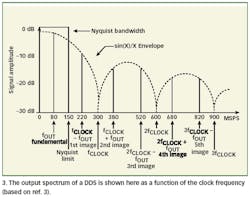
The set Ff and Fs - Ff is therefore a " couple" in sampled data (Fig. 3).
Their amplitude decreases because the DAC generates a sample-and-hold (S/H) waveform and not a sampled "delta function," so the amplitude is scaled by the S/H transfer function given by sin(x)/x, where x is 1/Fs (and therefore goes to zero at integer multiples of the sampling frequency Fs = Fclock in Fig. 3).
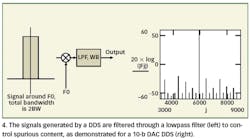
Negative frequencies are real physical phenomena and not just a mathematical outcome of the Fourier transform. When a signal in the vicinity of F0 is mixed with F0 itself (Fig. 4, left), the noise bandwidth of the lowpass filter is twice its bandwidth (BW) because all sidebands around F0 (BW) will pass into the filter. Signals above F0 will generate a positive output while frequencies below F0 will generate a negative output (Fig. 4, right).
Since the electrical signal in a DDS is a vector, positive and negative phases are possible, and positive and negative frequencies. If F0 + 1 or F0- 1 are mixed with F0, and the mixer output at 1 Hz displayed on an oscilloscope, it would be impossible to tell the difference between the two outputs. What is known is that the two signals are offset-by 180 deg. To identify them, two components of the vector must be displayed, hence the in-phase (I) and quadrature (Q) components.
The basic equations for a DDS, to generate sinewave outputs and change frequencies by changing the control input word based on a W-bit accumulator and a D-bit DAC (assuming Q > D + 1) include
the following:
Fout = W1 (Fclock/2W)
where:
W1 = the control input.
For example, a 48-b accumulator DDS, running at a clock frequency of 1000 MHz, has a frequency resolution of 109/248 ~ 3.5 Hz.
Spurious signals, which traditionally have been a limitation of DDS technology, are approximately given by -6D (dBc), or about -70 dBc for the 12-b DAC. (This is true mainly for clock frequencies below Fclock/4; above this clock rate, DAC errors begin to dominate.) A DDS source's switching speed is given by approximately 3/BW, where B is the output bandwidth of the lowpass filter.
The output frequency of a DDS is practically limited to 40 to 45 percent of the clock frequency, since the source generates both Fout and Fclock - Fout and there are limitations on how to filter Fclock - Fout as Fout gets closer to Fclock/2. This is a natural outcome of the sampling theorem that states that sampling rate must be at least two samples per cycle.
The frequency command words W1 and 2W- W1 will generate the same output frequency, although the two output signals will be offset by 180 deg. For an input command of W1, the accumulator increments W1, 2W1, 3W1...until it reaches 2W which is a complete cycle and 2W will then be subtracted from the sum (modulus 2π).
When controlling 2W - W1, the accumulator will almost always exceed its full state so the residue will be 2W - W1, 2(2W - W1), 3(2W - W1), etc...therefore: 2W - W1, 2W - 2W1, 2W - 3W1, etc. The absolute value of the phase increment (slope) is similar, but with opposite phase sign.
Page Title
If a second accumulator is added in front of the first accumulator, the phase generator is now a double accumulator, or a double integrator, and has a parabolic output. In the analog domain, this translates to sin(αt2) and since the instantaneous frequency of a signal is given by the derivative of the phase, it becomes 2αt, or a (linear FM) chirp signal. In the digital domain, this is of course the same, and linear FM signals have significant applications in the market; from imaging radars, test signals, optical imaging to instrumentation and silicon yield enhancement. The chirp DDS allows setting accurate and repeatable start, stop, and chirp-rate frequencies, not possible from analog voltage-controlled-oscillator (VCO) designs.
The overall principles of digitally generating chirp signals are very similar to DDS sinewave signal generation, with two distinct additional fundamental equations. The sweep rate is given by:
Sweep rate = W1× Fclock2/2W.
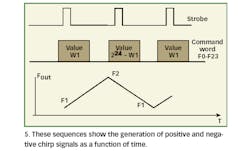
For example, for a chirp DDS with a 24-b accumulator (a model DCP-1 from Meret Optical Systems, for example) and 500 MHz clock rate, the minimum chirp rate, W1 = 1, is ~ 14.9 kHz/µs. Rather than negative frequency, a chirp generator can create chirps with negative slopes. Again, the pair W1 and 2W? W1 is a positive/negative slope pair. In the above example, the command 224 ? 1, which is FFFFFFF hex, will generate a negative chirp with a rate of ~ ?14.9 kHz/µs. The calculation of 224 ? W1 (to create a negative slope chirp) can be done by at least two ways: Subtract W1 from 224 or invert all digits of W1 and add 1. For example, for W1 = 1, which is 0000001 Hex, invert all digits (FFFFFFE) and add 1, for a total of FFFFFFF Hex. For W1 = 15, or 00000F, invert all digits (FFFFFF0) and add 1, for a total of FFFFFF1 Hex. Figure 5 shows a functional run of positive and negative chirps.
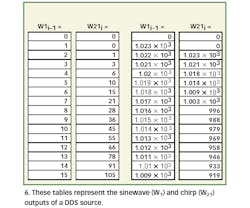
Figure 6 provides short tables of DDS and chirp accumulators for a 10-b accumulator and W1 = 001 hex and its pair FF3 (for 10-b digit arithmetic). In the tables, W1 is the DDS output while W21 is the chirper output.
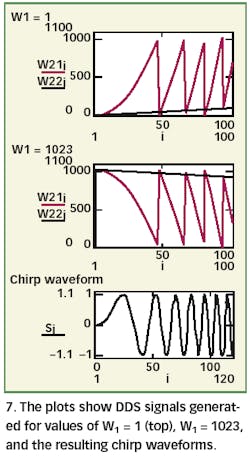
The phase ramps (where phase is modulus 2π, or 1024 in this case) are shown in Fig. 7 (where phase is denoted in red and frequency in blue color).
Quantization effects cause noise and spurious content in DDS signals. It is well known from DSP basics that the quantization signal-to-noise ratio (SNR) of a digitally generated signal is ~6D dBc, or ~?72 dBc for a 12-b DDS. This can be easily translated to phase noise since quantization noise is uniformly distributed across ~ Fclock. Generally, incremental DDS phase noise, caused by quantization errors, can be approximated by ?6D ? 10log(Fclock). For example, a 10-b DDS clocked at 320 MHz generates a phase-noise floor on the order of ?60 ? 85 = ?145 dBc/Hz. Some analog noise might be added due to DAC circuitry and a typical real number for such a DDS is closer to a still respectable ?135 dBc/Hz.
For all practical purposes, a DDS chirp source generates very accurate and repeatable chirps, and its linearity is as good as the quantization error, which is minimal. However, the lowpass filter that follows a DDS has phase characteristics that can affect chirp linearity. As the frequency changes, the output signal passes the lowpass filter, and as the filter's group delay deviates from linear phase, it will affect the frequency slope accuracy. Hence, filters with linear phase characteristics are highly recommended for the best chirp linearity.
This is usually not a problem up to about 20 percent of the output bandwidth or in cases that the chirp is generated across a small percentage bandwidth. But as the output frequency increases, the phase error and deviation from linear phase (filter dispersion) may require the use of a phase equalization network.
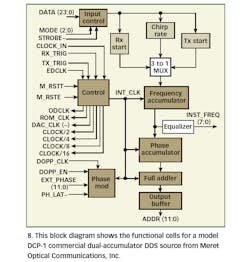
Certain utility functions in a DDS are convenient for many applications (Fig. 8) .
For example, the ability to shift phase (achieved by placing an adder after the phase accumulator) allows very precisely controlled phase modulation. It is also possible to set start and stop frequencies in chirp mode, and by control of instantaneous frequency, to allow setting thresholds or trigger certain events when these frequencies are reached (see INST_FREQ in Fig. 8). The ability to control the phase reset function of a DDS makes it possible to start the chirp at the same point in every run.
DDS and DDS chirp are mature technologies that enable fast switching, fine resolution, and excellent linearity in frequency sweeping requirements. While arbitrary waveform generation has advanced mightily in the last 15 years, allowing arbitrary signals stored in memory, the large size and expensive cost of such generators can be prohibitive for some applications compared to the small size of DDS and chirp DDS sources. The capability of a DDS source to change frequency while maintaining phase continuity, and the application of chirps for generating accurate positive and negative chirp slopes, has earned the technology a central and growing position in the signal-generation and frequency-synthesis space. Advanced CMOS DDS devices can now clock at 1 GHz (for output signals to 400 MHz), with GaAs devices offering more than double this speed.
REFERENCES
- Bar-Giora Goldberg, Digital Frequency Synthesis Demystified, LLH publishing, 1999.
- Analog Devices, Norwood, MA, data sheets for DDS product line.
- Meret Optical Communications, San Diego, CA, data sheet for DCP-1 Chirp Synthesizer.
- J. Tierney, C. Rader, and B. Gold, "A Digital Frequency Synthesizer," IEEE Transactions on Audio Electronics, pp. 48-57, 1971.5.
- B.G. Goldberg, Seminar notes for Besser Associates, www.bessercourse.com or www.cei.com.
This file type includes high resolution graphics and schematics when applicable.