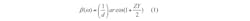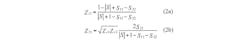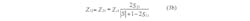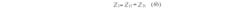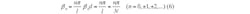This file type includes high resolution graphics and schematics.
Dual-frequency antennas play strong roles in many wireless products. These antennas can reduce the number of antennas needed in a portable wireless design, such as for personal communications systems (PCS) and wireless-local-area-network (WLAN) systems, while reducing the size and weight of a handheld device. A number of approaches have already been developed for producing dual-frequency antennas for such applications.1-3 For example, fractal antennas ave shown promise as compact multiband planar antennas.4 Based on conventional transmission lines (TLs), they typically include a single branch dispersion curve to form multiple paths with different resonant lengths at one-half or one-quarter-wavelength modes to obtain the multiple resonances needed for multiple-frequency operation. Other design approaches are also being explored, as the use of metamaterials based on periodic unit-cell structures for high-frequency antennas application has grown rapidly with the verification of left-handed (LH) metamaterials.5-11
Related Articles
• Antenna Aims At Dual Bands
• Dual-Band Coupler Links With CRLH Lines
• UWB Antenna Blocks Interference
Antennas fed by means of coplanar waveguide (CPW) can be easily incorporated with microwave integrated circuits (MICs) and monolithic microwave integrated circuits ((MMICs).12 In addition to the design freedoms they offer, CPW TLs suffer lower radiation loss and less dispersion than microstrip TLs. The use of a viahole-free structure and signal-layer process can yield a simpler fabrication process compared to many approaches used for producing metamaterial-based resonant antennas.6,7 By creating a structure with CPW feed and composite left/right hand transmission lines (CRLH TLs), it is possible to form compact antennas capable of dual-frequency operation. The design approach will be analyzed by means of computer-aided-engineering (CAE) software and verified by means of high-frequency measurements of key parameters, such as gain, impedance, and radiation pattern.
Figure 1 shows a CPW unit cell for a CRLH TL. To realize the left-handed inductance and capacitance, the meander lines are connected between the top patch and the CPW ground plane as the shorted stub and an interdigital line between the two top patches. The meander lines of the dual-frequency antenna are symmetrically aligned on both sides of the CPW ground. The CPW-fed dual-frequency antenna was designed as one unit cell and fabricated on low-cost P4BM-2 substrate material, available from a number of suppliers including Altechna. The P4BM-2 material, with circuit-board thickness of 1 mm, exhibits a dielectric constant of 2.2.
1. This diagram shows the basic structure of the CPW CRLH TL unit cell.
By applying the periodic boundary condition related with the Bloch-Floquet theorem to the unit cell, the dispersion can be obtained by means of Eq. 1:
In practice, the dispersion curves cannot be calculated directly; the Z-parameters must be transformed from the S-parameters by using relationships such as Eqs. 2(a)-(d):
Since the CRLH TL unit cell is a symmetrical structure, the circuit model for a lossless (R = 0 and G = 0) symetrical structure can be based on the structure of Fig. 1. The characteristic resistance of the structure, Zc1, is equal to Zc2, while the S-parameters, S11 is equal to S22 and S12 is equal to forward transmission, S21. As a result, simplified equations for the relationships of Eq. 2 can be expressed as Eqs. 3(a) and 3(b):
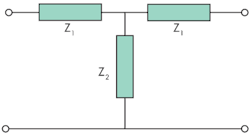
2. The CPW CRLH TL unit cell can be shown as a T-shaped equivalent network.
The structure can then be fashioned in the form of a T-shaped network (Fig. 2), using Eqs. 4(a) and 4(b):
Therefore, the relationship of Eq. 5 can be applied:
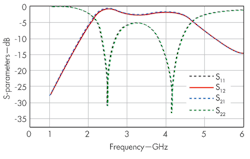
3. These are the simulated S-parameters of the CPW CRLH TL unit cell.
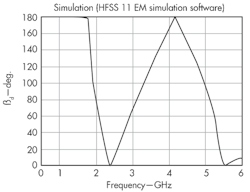
4. These are the dispersion curves of the CPW CRLH TL.
Figure 3 shows the full-wave S-parameters for the CPW CRLH TL unit, while Fig. 4 depicts the dispersion relationships calculated by Eqs. 3 through 5. For a balanced condition, where ωse = ωsh, the dispersion takes place in the LH and RH regions. When the length of the resonator is equivalent to a negative, zero, and positive resonant number times one-half wavelength, the resonances of an open-ended artificial CRLH TL resonator are achieved. This means that the propagation constants for an artificial CRLH TL for resonant mode (n) should be satisfied by Eq. 6:
where:
l = the physical length of the resonator;
n = the mode number of the resonator; and
N = the number of unit cells.
This file type includes high resolution graphics and schematics.
Putting It All Together
This file type includes high resolution graphics and schematics.
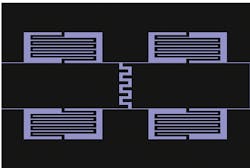
Figure 5 shows the designed and fabricated dual-frequency antennas. The CPW dual-frequency metamaterial antenna is composed of top metal patches, shorted meander lines, and a CPW ground plane. The feed line for impedance matching between the 50-Ω ports and the antenna circuitry is designed by impedance transition line and coupling capacitance. The antenna’s dimensions are as follows: antenna length, L = 28.6 mm; antenna width, W = 22.4 mm. The widths of the CPW feed lines are W1 = 3 mm, W2 = 0.4 mm, and W3 = 6 mm. The CPW trace length is L1 = 1 mm. The line lengths are L1 = 1 mm, L2 = 5.8 mm, L3 = 24.8 mm, and L4 = 0.6 mm. The gap between the CPW trace and the resonant antennas, g1, is 0.4 mm. The widths of the left-hand interdigital capacitors are g2 = 0.4 mm and g3 = 1 mm. The width of the left-hand shorted meander lines is g4 = 0.2 mm. Finally, the width of the left-hand gap between the CPW ground and the top patch is g5 = 0.2 mm.
5. The top diagram shows the basic layout for a dual-frequency antenna based on a CPW CRLH TL unit resonator, while the photograph on the bottom is a fabricated CPW CRLH TL dual-frequency antenna.
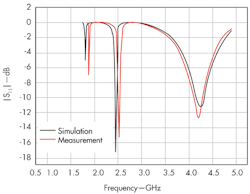
The fabricated antenna measures 22.4 x 28.6 mm. Its performance was modeled using the High-Frequency Structure Simulator (HFSS 11) electromagnetic (EM) simulation software from Ansoft/Ansys. Figure 6 shows the simulated and measured return losses of the antenna for a one-cell CPW CRLH TL. Variations found between the simulations and measurements stem from fabrication errors and dimensional tolerances. The resonant frequencies of the zero- and first-order modes were simulated (measured) at 2.45 GHz (2.50 GHz) and 4.25 GHz (4.20 GHz), respectively.
6. These plots show the simulated and measured return loss for the CPW CRLH TL dual-frequency antennas.
These measured and simulated results show good agreement with the theoretical results from the dispersion curves in Fig. 4. The reflection cofficient is lower than the lower and upper 10-dB bandwidths of 2.485 to 2.515 GHz and 4.16 to 4.34 GHz ; as a result, 10-dB bandwidths of 1.2 and 4.2%, respectively, were achieved for the fabricated antenna. The electrical size of the CRLH TL’s unit cell is 0.254λ0 x 0.258λ0 at 2.54 GHz. The overall size of the antenna is approximately 0.331λ0 x 0.258λ0 x 0.011λ0.
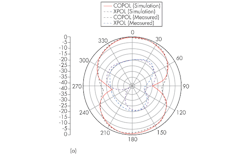
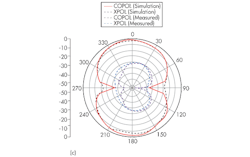
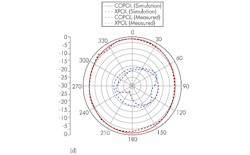
Figure 7 shows the simulated and measured radition patterns of the antenna at in its zero- and first-order resonant modes, which are the E-plane (y-z plane) and H-plane (x-z plane) modes at 2.5 and 4.2 GHz. The measured and simulated results agree closely. Maximum gains for the dual-frequency antenna in the E-plane (y-z plane) were simulated as 2.31 dBi at 2.5 GHz and 3.52 dBi at 4.2 GHz, compared to measured maximum gains of 1.85 dBi at 2.5 GHz and 3.05 dBi at 4.2 GHz. The radiation patterns show that the antenna’s measured cross-polarization levels are higher than the simulated cross-polarization levels. These differences are also due to the fabrication limitation resulting from the fine meander lines, as well as the measurement error resulting from the much smaller size of the aperture, compared with that of the RF cable in the test environment.
7. These simulated and measured responses show the antenna’s zero- and first-order mode responses for its E- and H-plane patterns: (a) zero-order in E-plane, (b) zero order in H-plane, (c) first order in E-plane, and first-order in H-plane.
This file type includes high resolution graphics and schematics.
Conclusions And References
This file type includes high resolution graphics and schematics.
Related Articles
• Antenna Aims At Dual Bands
• Dual-Band Coupler Links With CRLH Lines
• UWB Antenna Blocks Interference
By analyzing and simulating the dual-frequency antenna based on CPW CRLH TLs, it was found that the antenna could be reduced further in size. By designing such resonant antennas with CPW technology, a great deal of design freedom is provided in relation to the shunt parameters in the equivalent-circuit model. This novel antenna design can help reduce the size of different wireless products, including those normally requiring separate antennas—such as products with PCS and WLAN capabilities.
Acknowledgement
This work was supported by the National Natural Science Foundation of China (Grant No. 60971118).
Zheng Long, Engineer
Wang Guangming, Engineer
Geng Lin, Engineer
Microwave Lab, Air Defence and Anti Missile Institution of Air Force Engineering University, Xi’an Shaanxi Province 710051, People’s Republic of China.
References
1. Shun-Lai Ma and Jeen-SheenRow, “Design of Single-Feed Dual-Frequency Patch Antenna for GPS and WLAN Applications, IEEE Transactions on Antennas & Propagation, Vol. 59, No. 9, September 2011, pp. 3433-3436.
2. Mrinal Kanti Mandal and Zhi Ning Chen, “Compact Dual-Band and Ultrawideband Loop Antennas,” IEEE Transactions on Antennas & Propagation, Vol. 59, No. 8, August 2011, pp. 2774-2779.
3. Óscar Quevedo-Teruel, Elena Pucci, and EvaRajo-Iglesias, “Compact Loaded PIFA for Multifrequency Applications,” IEEE Transactions on Antennas & Propagation, Vol. 58, No. 3, March 2010, pp. 656-664.
4. Jianhua Zhou, Yong Luo, Baiqiang You, and BinLin, “Three to two curve fractal folded dipole antenna for RFID application,”Microwave and Optical Technology Letters, Vol. 52, No. 8, August 2010, pp. 1827-1830.
5. C. Caloz and T. Itoh, Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications, Wiley, NewYork, December 2005.
6. S. Otto, A. Rennings, C. Caloz, P. Waldow, and T. Itoh,“Composite Right/Left-Handed7. Anthony Lai, Kevin M.K.H. Leong, and Tatsuo Itoh,“Infinite Wavelength Resonant Antennas With Monopolar Radiation Pattern Based on Periodic Structures,” IEEE Transactions on Antennas & Propagation, Vol. 55, No. 3, March 2007, pp. 868-876.
8. Jae-Hyun Park, Young-Ho Ryu, Jae-Gon Lee, and Jeong-Hae Lee,“Epsilon Negative Zeroth-Order Resonator Antenna,” IEEE Transactions on Antennas & Propagation, Vol. 55, No. 12, December 2007, pp. 3710-3712.
9. Young-Ho Ryu, Jae-Hyun Park, Jeong-Hae Lee, and Heung-Sik Tae,“Multiband Antenna Using +1,-1,and 0 Resonant Mode of DGS Dual Composite Right/Left Handed Transmission Line,”Microwave and Optical Technology Letters, Vol. 51, No. 10, October 2009, pp. 2485-2488.
10. Taehee Jang, Aehyurk Choi, and Sungjoon Lim,“Compact Coplanar Waveguide (CPW)-Fed Zeroth-Order Resonant Antennas With Extended Bandwidth and High Efficiency on Vialess Single Layer,” IEEE Transactions on Antennas & Propagation, Vol. 59, No.2, February 2011, pp.363-372.
11. Chien-Pai Lai, Shih-Chia Chiu, Hsueh-Jyh Li, and Shih-Yuan Chen,“Zeroth-Order Resonator Antennas Using Inductor-Loaded and Capacitor-Loaded CPWs,” IEEE Transactions on Antennas & Propagation, Vol. 59 , No. 9, September 2011, pp. 3448-3453.
12. Bratin Ghosh, S.K. Moinul Haque, and Debasis Mitra, “Miniaturization of Slot Antennas Using Slit and Strip Loading,” IEEE Transactions on Antennas & Propagation, Vol. 59, No. 10, October 2011, pp. 3922-3927.
This file type includes high resolution graphics and schematics.