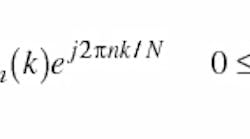Establish Test Procedures For WiMAX Transceivers

Data-intensive wireless applications have sped the development of multicarrier modulation techniques, such as orthogonal frequency-division multiplexing (OFDM). OFDM can overcome many problems that arise with high-bit-rate communications, such as time dispersion.^1-4

Because OFDM is becoming so widespread, with applications in European Hiperlan, US wireless local-area networks (WLANs, such as IEEE 802.11a/g standards), in wireless metropolitan-area networks (WMANs), and especially in emerging WiMAX applications, it would be useful to understand the workings of a WiMAX transceiver design and how to test it. What follows is the first part of a three-part series on WiMAX transceiver design and performance evaluation strategies.

In OFDM-based WiMAX systems, carrier frequencies are chosen to avoid interference with and from other carrier frequencies. The data-bearing symbol stream is split into several lower-rate streams and these are transmitted on different carriers. Since this increases the symbol period by the number of nonoverlapping carriers (subcarriers), multipath will only affect a small portion of the neighboring symbols. The remaining intersymbol interference (ISI) can be removed by cyclically extending the OFDM symbol.⁵The length of the cyclic extension should be at least the maximum excess delay of the channel. In this way, OFDM reduces the effect of multipath channels encountered with high data rates and avoids the use of complex equalization schemes.

Recently, OFDM has been applied to WMAN systems for fixed wireless access. The IEEE 802.16-2004 WMAN standard,⁶which operates in bands between 2 and 11 GHz and higher, specifies a metropolitan-area networking protocol that will enable a wireless alternative to cable, DSL, and T1 services for last-mile broadband access as well as providing backhaul for IEEE 802.11 WLAN hotspots. In addition, efforts are underway to adopt OFDM for mobile WMAN,⁷fourth-generation (4G) cellular systems, and wireless personal-area networks (WPANs).

While OFDM is an effective modulation method, it has its deficiencies. Several impairments can degrade the performance of OFDM if the system and its transceivers are not properly designed. Practical integration of RF and baseband circuitry in these systems requires realistic testing and verification procedures and equipment. This involves incorporation of testing and measurement capabilities of the standard based WiMAX signals into the measurement receivers (such as vector signal analyzers). Representative test signals, including standards-based in-phase (I) and quadrature (Q) baseband samples, must be generated for use with test equipment such as the Signature signal analyzer from Anritsu Co. (www.us.anritsu.com).

More effective WiMAX transceivers can be designed by incorporating test mechanisms into the transceiver integrated circuits (ICs). For the purpose of this investigation, digital baseband transceivers for IEEE 802.16-2004 WMAN system will be studied. By examining the block diagram of a standard transmitter and a receiver proposed by the authors, measurement points can be identified and evaluated for their impact on performance. This study will review transceiver performance under various noise and impairment scenarios, and various measurement techniques for identifying different sources of noise and impairments.

The IEEE 802.16-2004 standard defines the physical-layer (PHY) and media-access-control (MAC) protocols for broadband wireless access (BWA). The standard introduces three major air-interface formats for frequencies below 11 GHz, namely: WirelessMAN-SC PHY (single carrier modulation), WirelessMAN-OFDM PHY (OFDM-256), and WirelessMAN-OFDMA PHY (OFDMA-2048). Among these three options, the WiMAX Forum has selected OFDM-256, which will be the focus of this study.

The standard defines different duplexing options, including time-division duplex (TDD), frequency-division duplex (FDD), or half-duplex frequency-division duplex FDD (H-FDD) formats. In licensed bands, the duplexing method shall be either TDD or FDD, while unlicensed operation is limited to the TDD format.

The OFDM-256 air interface offers many adaptive features as well as optional features. The adaptive features include the adaptation of modulation/coding format and adaptation of the cyclic prefix. A receiver should be able to demodulate a signal with different modulation formats as well as a signal with various transmission parameters. The standard includes some optional PHY features, such as space-time-coding (STC), adaptive antenna arrays, and subchannelization. It is unlikely that these optional features will be implemented in early products, and were not high in priority when developing a measurement strategy for OFDM-256. Therefore, this study includes only the required transceiver specifications, with optional features left for future study.

Page Title

In terms of operating carrier frequency and transmission bandwidth, IEEE 802.16-2004 provides a wide variety of options. However, the proposed baseline PHY receiver algorithm design is not affected by variation in carrier frequency and bandwidth. However, advanced receiver algorithms might take advantage of these variations and employ better baseband algorithms depending on the operating frequency and bandwidth. In this work, a generic baseline receiver algorithm design is proposed that works fairly well over different operation frequencies. Improvements on the receiver algorithms, which can take a priori information into account, are left for a future study.

The WiMAX Forum (www.wimaxforum.org) has the mission of ensuring the interoperability, promoting the IEEE 802.16 standard, and helping grow the overall market acceptance for IEEE 802.16 as a BWA standard. However, one of the Forum's first deliverables is to establish specific conformance procedures and testing labs to administer the testing. This process will result in "WiMAX certified" products that have guaranteed interoperability with other WiMAX certified solutions.

In developing a WiMAX system model, the transmitter's signal format must be adequately described, including frame formats (downlink and uplink subframes), OFDM symbol formats (for preamble and data symbols), standards based baseband transmitter blocks, and basic model of the transmitted signal itself. The frame format is like a traditional packet-based structure that uses a preamble and header followed by data bursts. In a standard downlink frame

(Fig. 1), the base-station transmits a preamble (long preamble that has a two OFDM symbol length), header, and multiple downlink bursts that are assigned to different users. Optionally, midambles (not shown in Fig. 1) can also be inserted before some bursts. In the uplink (UL), a preamble (short preamble which has only one OFDM symbol length) is used for each uplink burst transmitted by a user. Each uplink transmitter is assigned a time slot to transmit its burst in a time-division-multiplexing (TDM) manner. Similarly, in the downlink, a TDM type approach is employed (Fig 1). As mentioned previously, the uplink and downlink subframes can be configured as TDD, FDD, or H-FDD. In TDD mode, a short gap is placed between the DL and UL subframes (transmit-receive-transition-gap or TTG). After completion of the UL subframes, another short gap is added between this subframe and the next DL subframe (receiver-transmit-transition-gap or RTG).

Each preamble, header, and burst is made up of one or more OFDM symbols. Modulation on the OFDM carriers is binary phase-shift keying (BPSK), quadrature phase-shift keying (QPSK), 16-state quadrature amplitude modulation (16QAM), or 64QAM. Depending on the link quality between the transmitter and receiver, an appropriate modulation is selected for individual data bursts. Particularly interesting is the ability of using different modulation formats on each data burst. The information bits are mapped into data symbols depending on the used modulation type. The serial data symbols are then demultiplexed into parallel blocks and inverse-fast-Fourier-transform (IFFT) is applied to these parallel blocks to obtain the time-domain OFDM symbols. In OFDM-256, the number of subcarriers is 256. There are three types of subcarrier assignments: data, pilot, and null. In a regular OFDM symbol, 200 subcarriers are used for data and pilot, and the remaining 56 carriers are nulled for providing guard bands and dealing with carrier leakage which renders the DC carrier unusable. Of the 200 subcarriers, eight of these are used as pilot subcarriers, and these pilots are inserted at regular interval among the other data subcarriers which make up the remaining 192 active carriers. Figure 2 shows the carriers in the frequency domain.

Figure 3 shows the block diagram of a basic digital baseband transmitter. The information bits from the upper layers of the protocol stacks are first passed through a channel coding which consists of three blocks: randomizer, forward-error-correction (FEC) block, and interleaver. Data randomization is performed on each burst of data on the downlink and uplink. A FEC block, consisting of the concatenation of a Reed-Solomon (RS) outer code and a rate-compatible convolutional inner code, must be supported on both uplink and downlink. On the other hand, support of block-turbo coding (BTC) and convolutional-turbo-coding (CTC) are optional.

Page Title

In this study, only the mandatory coding schemes are employed, and the optional coding schemes are left for a future study. The encoding is performed by first passing the data in block format through the RS encoder and then passing it through a zero-terminating convolutional encoder. All encoded data bits are interleaved by a block interleaver with a block size corresponding to the number of coded bits per the allocated subchannels per OFDM symbol. The interleaver is defined by a two step permutation. The first ensures that adjacent coded bits are mapped onto nonadjacent subcarriers. The second permutation ensures that adjacent coded bits are mapped alternately onto less or more significant bits of the constellation, thus avoiding long runs of less reliable bits.

The bits after the channel coding are mapped to symbols, depending on the type of modulation used. As mentioned above, four different modulation options are available; BPSK, QPSK, 16QAM, or 64QAM. The constellationmapped data symbols are then mapped onto all allocated data subcarriers (the 192 data carriers in Fig. 2) in order of increasing frequency offset index. The first symbol out of the data constellation mapping is mapped onto the allocated subcarrier with the lowest frequency offset index. The pilot subcarriers (the 8 carriers in Fig. 2) are multiplexed into these data carriers in order to constitute the symbol. Note that BPSK modulation is used for the modulation of pilot carriers.

Once all the subcarriers that will form a full OFDM symbol have been populated, the serial data symbols are then converted to parallel blocks, and an Inverse Fast Fourier Transform (IFFT) is applied to these parallel blocks to obtain the time-domain OFDM symbols. Time-domain samples of an OFDM symbol can be obtained from frequency-domain symbols as:

where:

X_m(k) = the modulated data on the k_th subcarrier of the m_th OFDM symbol and

N = the number of subcarriers (for OFDM-256, N=256).

The guard interval also commonly referred to as cyclic prefix is a copy of the end of the symbol that is appended to the beginning of the symbol. Cyclic prefix is used to mitigate the effect of time dispersion and its duration has to exceed the maximum excess delay of the channel in order to avoid ISI.⁸ As long as maximum excess delay (t_max)is smaller than the length of the cyclic extension (T_g), the distorted part of the signal from the previous OFDM symbol will stay within the guard interval which will be removed later. Therefore, ISI will be prevented. Figure 4 shows the power spectral density and power versus time plots of the transmitted signal. The plots were generates from I/Q samples captured with the "Signature" real-time signal analyzer from Anritsu Co. (www.us.anritsu.com).

Frequency offset is a critical factor in OFDM system design. It results in intercarrier-interference (ICI) and destroys the orthogonality of subcarriers. Any difference between transmitter and receiver local oscillators will result in a frequency offset. This offset is usually compensated for by using adaptive frequency correction (AFC), however any residual errors result in a degraded system performance. The frequency offset is introduced in time-domain signal as shown below:

where: y(n) = the baseband received signal (with frequency offset error) and Y(k) = the recovered data symbols. After some analysis, it is possible to relate the recovered symbols, Y_m(k), to the originally transmitted symbols, X_m(k). The effect of frequency offset on time-domain signal X_m(n) will be a time-dependent phase shift:

where:

The first term in Eq. 2 is equal to the originally sent symbol multiplied with attenuation and a phase rotation term that depends on and the OFDM symbol index (it does not depend on carrier index k so the effect of frequency offset on the carriers will be the same for all carriers). Therefore, this term S(k,k) introduces a constant phase shift of 2p m(N_s/N) and an attenuation of sin (p)/p in magnitude. In addition to the attenuation of desired symbols, there is interference between subcarriers. The second term in Eq. 2 represents the interference from other sub-carriers which is often referred as ICI.

Page Title

Figure 5 shows the effect of frequency error in the constellation of received symbols. Notice that frequency error introduces phase rotation as given above as well as interference (ICI). Phase rotation can be handled by simple pilotbased, phase-tracking techniques. But, ICI needs more attention and requires more advanced receiver algorithms. Therefore, accurate frequency offset estimation is a very important part of the OFDM receiver design.

The effect of symbol time offset for OFDM is the rotation of the symbols and, if large, ISI. Rotation of symbols can be folded into the estimated channel and corrected easily if timing offset is smaller than the unused part of the cyclic prefix.

Using the same notation in frequency offset case, transmitted symbols are represented with X(k) and the baseband equivalent of the time-domain signal is represented with x(n):

The symbol timing error is caused by assuming the wrong starting position of the OFDM symbol. So y(n) will be nothing but the shifted version of x(n) in time domain, i.e., with a timing error of θ, the result is:

Here the sign of θ depends on whether sampling occurs before the exact time or after the exact time. Parameter Y(k) can be calculated from y(n) using DFT:

Equation 3 shows that a timing offset of θ causes only a rotation on the recovered data symbols. The value of the recovered symbol depends only on the transmitted data, but not the neighboring carriers. This means that the symbol timing error does not destroy the orthogonality of carriers and the effect of timing error is a phase rotation, which linearly changes with carriers' order.

The clock-timing difference in the transmitter and receiver causes sampling timing error. The sample timing error can be ignored for small number of carriers and when the number of symbols within the subframe is not large. The sample timing error causes a carrier-and symbol-dependent rotation in the received symbols. With sample timing error, it is possible to relate the recovered symbols to the actual transmitted symbols as:

where:

b = the relative clock deviation of the reference oscillator and N_s=N+N_g, with N_g being the number of samples used for cyclic prefix.

Notice that the rotation increases as the carrier and symbol index grows. In other words, the effect of sample timing error will be more in the higher indexed subcarriers and in the later symbols of the subframe (assuming that no midambles are used).

Figure 6 shows a representative example of the effect of sample timing offset in OFDM systems. The sample timing offset effect increases further from the center carrier (zero carrier index). Also, notice the increase of the average EVM (averaged over all carriers) as the symbol index increases.

Phase noise is introduced by the local oscillator (LO) in any receiver and can be interpreted as a parasitic phase modulation in the oscillator's signal. Phase noise can be modeled as a zero mean random variable. Assuming the channel is flat and the signal is only affected by phase noise Φ(n) at the receiver, the received time-domain signal can be written as:

Page Title

Assuming that the phase offset is small, e^jφ⁽ⁿ⁾1 + jφ(n), the recovered symbols will have the form:

In Eq. 6, the common phase term introduces a rotation to the constellations. This rotation is the same for all subcarriers (so it can be corrected by using a pilot-based phase tracker) and is representative of the average phase noise.

The last term in Eq. 6 represents the leakage from neighboring subcarriers to the useful signal of each subcarrier, i.e. ICI. This term cannot be corrected since both phase offset, φ_m,(n), and input data sequence, X_m(n), are random. Therefore, it will cause SNR degradation of the overall system. The only way to reduce interference due to this term is to improve the performance of the oscillator (usually with an associated increase in cost). A more detailed study of the effects of phase noise on OFDM system can be found in refs. 9 and 10.

One of the major problems with OFDM modulation technique is that it has high peak-to-average power ratio (PAPR) that requires power amplifiers (PAs) in the system with wide dynamic range to minimize distortion. The technique of "backing-off" from full output levels is often used in wireless-communications systems to ensure linear operation. However, this approach sacrifices efficiency and increases power consumption. Alternatively, baseband linearization techniques, which predistort the signals to be amplified, can compensate for nonlinear effects. The efficiency and adaptation of the linearization algorithms is the key to the success of the processing.

Nonlinear PAs cause in-band and out-of-band distortion, with serious impact to communication quality. Common parameters used to describe the PA nonlinearities include AM-AM distortion, AM-PM distortion, 1-dB compression point (PldB), and third-order intercept point (IP3). Typical parameters used to evaluate the effects of the model on a system are error vector magnitude (EVM) and adjacent-channel power ratio (ACPR).

The impairment caused by PAs is related to the PAPR measurement. Discrete-time PAPR of m_th OFDM symbol x_m is defined as:¹¹

where:

E{} = the expected value operation.

Although the PAPR is very large for OFDM, high-magnitude peaks occur relatively rarely and most of the transmitted power is concentrated in signals of low amplitude, e.g., maximum PAPR for an OFDM system with 32 carriers and QPSK modulation will be observed statistically only once in 3.7 million years if the duration of an OFDM symbol is 100 s.¹² Therefore, the statistical distribution of the PAPR should be taken into account.

The complementary cumulative distribution function (CCDF) is a useful statistical tool in evaluating signal power distribution properties. It is defined as the probability that the signal is at or higher than a given amplitude. Due to the power envelope of the OFDM signal not being constant; CCDF is useful for showing peak-to-average statistics for the signal under test. The CCDF curve could be used to detect whether the signal under test is clipping or not.

CCDF plots use units of percent for the y-axis and power (dB) for the x-axis. Power on the x-axis is relative to the signal average power, so 0 dB is the average power of the signal. Therefore, a marker readout of 2 dB 12 percent means there is a 12-percent probability that the signal power will be 2 dB or more above the average power.

Note that PA gain can also change in time, which causes a variation of the amplitude in the received signal. When there is a variation in gain, the recovered symbols can be related to the actual transmitted symbols as:

where:

g_m= the time-varying gain for each OFDM symbol index with respect to the reference gain in the preamble symbol (where the channel coefficients are estimated).

Page Title

As mentioned earlier, one of the main reasons OFDM has been promoted for high data rate communication systems is that it has the ability to work in highly dispersive channels. The time dispersion will cause the channel to be frequency selective. However, by splitting the total transmission bandwidth to narrower channels, it is ensured that within each subchannel the channel frequency response is flat. Therefore, if the receiver is able to estimate the channel response over each carrier, the effect of channel dispersion (frequency selectivity) can be removed easily.

If the channel is assumed to be varying slowly in time (which is a valid assumption for low mobility and fixed wireless applications), the received signal at each carrier can be represented as:

where:

H(k) = the complex channel frequency response (which is assumed to be constant within a subframe).

Note that the response is carrier dependent. However, the variation across the carriers is smooth (i.e., the channel responses in closely spaced carriers are not independent). The memory across the carriers can be used to develop improved channel-estimation algorithms.

In this study, all the interference sources (including co-channel, adjacent channel, inter-carrier interferences, etc.) are folded into the additive white Gaussian noise (AWGN) term to simplify receiver design and analysis. In future studies, the authors intend to treat these interference sources differently so that we can exploit the color and structure of the interferer to design better transceiver algorithms. When all the additive interfering sources are folded into AWGN term, the received signal can be represented as:

where:

Z_m(k) = the AWGN term.

The transmitted signal, that goes through the I/Q vector modulator, experiences several levels of signal distortion due to imperfection in the modulator. These distortions can greatly affect the performance of the received signal and the overall system performance. The major I/Q impairments can be classified as I/Q offset, I/Q gain imbalance, and I/Q quadrature-error. Note that the I/Q impairments in the received signal will have quite different impact on OFDM based systems compared to the conventional single-carrier systems.

I/Q offset, also called I/Q origin offset-or carrier leakage, indicates the magnitude of the carrier feedthrough. I/Q Offset can be observed as an offset in the constellation. Gain mismatch or gain imbalance will result in the amplitude of one channel being smaller that the other. By comparing the gain of the I signal with the gain of the Q signal, 20log(I_scale/Q_scale), the I/Q gain imbalance can be obtained.

Next month, this discussion on developing a receiver for testing WiMAX will continue with an approach for modeling baseband I/Q origin offset (Fig. 7) and I/Q gain imbalance (Fig. 8) as part of a time-domain signal.

Editor's Note: This is the first installment in a three-part article. Next month, the authors will examine the structure of a proposed receiver for testing WiMAX products, along with algorithms necessary for performing packet detection and symbol estimation.

ACKNOWLEDGMENT

The authors would like to thank Dr. Larry Dunleavy for his comments and for the review of this article prior to publication.

REFERENCES

A.R.S. Bahai, B.R. Saltzberg, and M. Ergen, Multi-Carrier Digital Communication: Theory and Applications of OFDM, Kluwer Academic/Plenum Publishers, New York, 1999.
R. Prasad and R.V. Nee, OFDM for Wireless Multimedia Communications, Artech House, Norwood, MA, 2000.
M. Engels, Wireless OFDM Systems: How to Make Them Work, Kluwer Academic Publishers, New York, 2002.
J. Heiskala and J. Terry, OFDM Wireless LANs: A Theoretical and Practical Guide, Sams Publishing, Indianapolis, 2002.
H. Beigi, S. Maes, and J. Sorenson, "The cyclic prefix of OFDM/DMTAn Analysis," in International Zurich Seminar on Broadband Communications Access, Transmission, Networking, Zurich, Switzerland, 2002, pp. 1-3.
IEEE Standard for Local and Metropolitan Area Networks, Part 16: Air Interface for Fixed Broadband Wireless Access Systems, Standard IEEE 802.16-2004, The Institute of Electrical and Electronics Engineers, New York, 2004.
IEEE 802.16e, "Mobile WirelessMAN," http://www.eee802.org/16/tge/index.html.
F. Tufvesson, "Design of wireless communications systemsissues on synchronization, channel estimation, and multicarrier systems," Ph.D. dissertation, Lund University, Lund, Sweden, 2000.
A.G. Armada, "Understanding the effects of phase noise in orthogonal frequency division multiplexing (OFDM)," IEEE Transactions on Broadcasting, Vol. 47, No. 2, June 2002, pp. 153-159.
K. Sathananthan and C. Tellambura, "Performance analysis of an OFDM system with carrier frequency offset and phase noise," in Proceedings of the IEEE Vehicular Technology Conference, Vol. 4, Atlantic City, NJ, October 2001, pp. 2329-2332.
S. Muller and J. Huber, "A comparison of peak power reduction schemes for OFDM," in Proceedings of IEEE Globecom Conference, Vol. 1, Phoenix, AZ, 1997, pp. 1-5.
H. Ochiai and H Imai, "On the distribution of the peak-toaverage power ratio in OFDM signals," IEEE Transactions on Communications, Vol. 49, No. 2, February 2001.
P.H. Moose, "A technique for orthogonal frequency division multiplexing frequency offset correction," IEEE Transactions on Communications, Vol. 42, No. 10, October 1994, pp. 2908-2914.
P. Panagiotou, A. Anastasopoulos, and A. Polydoros, "Likelihood ratio tests for modulation classification," in Proceedings of IEEE Military Communications (MILCOM) Conference, Vol. 2, Los Angeles, CA, 2000, pp. 670-674.
B.G. Mobasseri, "Constellation shape as a robust signature for digital modulation recognition," in Proceedings of IEEE Military Communications (MILCOM) Conference, Vol. 1, Atlantic City, NJ, 1999, pp. 442-446.
T. Keller and L. Hanzo, "Blind detection assisted sub-band adaptive "Turbo-coded OFDM schemes," in Proceedings of IEEE Vehicular Technology Conference (VTC), Vol. 1, Houston, TX, 1999, pp. 489-493.