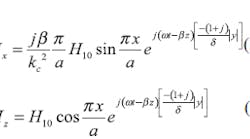Due to the decreasing skin depth of printed-circuit boards (PCBs) used for high-speed analog and digital circuits, surface roughness plays an important role in determining electrical performance. The effect of roughness on power dissipation has been considered an electromechanical coupling (EC) issue, studied by simultaneous mechanical and electromagnetic (EM) analyses, but with limited success. So, an EC model was developed as an effective analysis approach for evaluating the effect of surface roughness on power dissipation.
The EC model was developed by introducing the concept of a technical index and a measurement method for validation. Using the EC model as the boundary condition, a generic formula for added power dissipation caused by surface roughness will be deduced. Simulations and experiments will also be performed to validate the model. A typical EC model will be used to describe the surface roughness effect of electrical conductors, and that model itself will be improved by a two-dimensional fractal function. The conventional Monte Carlo method and finite-element method (FEM) were enlisted for the EC calculations. Comparative results will show the EC model can describe surface roughness more precisely than other models. Its advantages on the computational efficiency can be demonstrated by a comparison in centralprocessing- unit (CPU) time based on the same computational conditions. The EC model was found to be ideal for describing the surface roughness of high-frequency circuits, meeting various requirements for mechanical analysis and EM calculation.
Smooth surfaces are rare in nature, and most surfaces (including engineering surfaces) appear rough when viewed under a microscope. Since electronic products and systems have been steadily increasing to analog and digital rates in the gigahertz region, the surface roughness of the PCBs used in those designs can have significant impact on key electrical properties, such as power dissipation. As a result, a quantitative description of a PCB's surface topography is vital to understanding surface effect on electrical performance.
During the past decade, numerous methods have been developed to quantitatively analyze surface topography, including numerical solutions,1 theoretical approaches,2 and experimental approaches.3 Unfortunately, the process of acquiring measured profiles results in irreversible damage to the material under investigation, making it difficult if not impossible to complete a measured analysis of the rough surface of a PCB. In terms of computer-aided-engineering (CAE) analysis, existing commercial software tools do not model the inner surface roughness accurately. As a result, attention has been focused on numerical simulations of the inner surface roughness of circuit materials.
Present research on modeling surface roughness focused on mechanical approaches, effect on conductor impedance, and EM scattering. Mechanical modeling has relied on the geometric deviation description model in mechanical engineering as a means of evaluating the surface roughness of an electronic material.1,4,5 The approach was suitable for evaluating any friction at a material interface, any wearing of moving surfaces, sealing of joined surfaces, and reliability of a mated surface, but it did not take into consideration the effect of surface roughness on the EM characteristics. For evaluating the impedance of conductors, common results were due to Morgan's classical paper6 and the Hammerstad and Bekkadal formula.2 Moreover, recent results were also consistent with Morgan's work.7 In these works, a common and basic assumption was the lateral uniformity of the material under study, which indicated that the surface roughness was distributed in one direction and the surface was smooth along the direction of conducting current. However, this is a greatly oversimplified assumption, since any material fabrication process would invariably produce conductors with surface variations and the roughness distributed without predictable regularity.
In terms of studying EM scattering, Falconer8 and Mandelbrot9 showed that the multiscale nature of surface roughness could be represented by fractal geometry since the actual surface of an electrical material has a self-affinity property in nature.10 Increased detail about a material's rough surface could be gained by repeatedly magnifying its profile. But this additional roughness information has brought about a marked increase in the complexity of any computation and analysis performed on a material's surface roughness, and EM modeling disregarded the inter-relationships of surface roughness with electrical performance, greatly limiting the applicability of the modeling approach.
Because the effect of surface roughness on power dissipation is not only a problem in mechanical analysis but in EM analysis, it is considered an EC problem, requiring both mechanical and electrical parameters for complete analysis. Proekt and Cagellaris have formulated an effective conductivity by equating the power loss in a rough surface conductor with the loss for a smooth surface.11 However, their derivation, which was based on perturbation theory, was valid only when the surface roughness was far smaller than the skin depth, which was not adaptable when the surface roughness is comparable to skin depth. As a result, an EC modeling approach was developed for generic use with different surface roughness configurations while also meeting the different requirements for mechanical and EM calculations. It has been applied with good results for accuracy and computational efficiency.
Figure 1 shows a comparison of current flowing on smooth (top) and rough (bottom) surfaces. Based on microwave surface theory, 98.2 percent of current flow is concentrated within 4t (wavelengths) of the surface of a material.12-14 Therefore, the current flowing 4t from the surface was considered as a more reasonable view. The effect of roughness on the surface of a conductor depends on the ratio of the root mean square (RMS) surface roughness to the skin depth of the conductor, rather than the exact shape of the conductor's surface profile. Grades of roughness that were too large or too small relative to this 4t reference point had little influence on the material's electrical properties.
According to microwave surface resistance and engineering practices, a microfluctuating shape characteristic with an amplitude less than 0.5 times the skin depth would not have adverse effect on the material's electrical properties.15 This indicates that some numerical filtering of the original surface contours was needed. A modified profile was obtained by filtering out shortwave surface components having an amplitude of less than 0.5 times the skin depth. By this technique, the modeling method was called the EC modeling approach.
In terms of mechanical roughness modeling, in which only one dimension of local information is applied, the arithmetical mean deviation (Ra) is regarded as the unique evaluation index. Using such a parameter does not make it possible to fully consider two- or three-dimensional surface features, however. In such cases, parameter Ra is nondeterministic because the different surface contours may have the same Ra value. To perform EM modeling of surface roughness, two parameters (D and b) were introduced to describe the roughness of surfaces. Parameter D represents the fractal dimension, while parameter b is the fundamental frequency in space and determines surface density. Although these two parameters can describe surface roughness accurately, they cannot be measured directly and it is hard to represent them in terms of measured parameters of roughness, such as Ra. For this reason, mechanical roughness modeling has limited applicability for analyzing roughness effects on electrical performance. Studies have shown that the biggest differences for contours with the same Ra values were the density and the regularity of the surface peaks and valleys. Such information appears as the expansion length of the surface profile, which was the root reason for increasing the surface current path. Therefore, two parameters, Ra and R1, were introduced as a two-dimensional surface roughness index. Parameter Ra is the arithmetical mean deviation, while parameter R1 is an auxiliary parameter equal to the length of the effective contour. The two parameters are found by Eqs. 1 and 2, where:
l = one sampling length,
f(x) = effective conductive contour,
(xi, yi) = the measured value of the conductive contour, and d = the skin depth.
Using the two-dimensional roughness technical index a,R1> to describe surface microgeometry errors not only reflects the relief intensity of the roughness, but also reflects the fluctuational gradient of the roughness, in agreement with requirements of mechanical and EM field analysis.
Power dissipation according to a rough surface can be better understood by considering a rectangular waveguide. The transverse electromagnetic TE01 fundamental mode of the waveguide has a magnetic field in the narrow wall of the waveguide with HX and HZ components while the magnetic field in the narrow wall of the waveguide only has the HZ component. Considering the presence of loss, the HX and HZ components can be found from Eqs. 3 and 4:
According to skin effect theory,12-14 and Morgan's classical empirical formula,6 the added power dissipation by the roughness of the one unit infinitesimal element in the broad wall of the waveguide can be found from Eq. 5, while the added power dissipation by the roughness of the one infinitesimal unit in the narrow wall of the waveguide can be found from Eq. 6.
Continue on page 2
Page Title
Roughness is distributed throughout an inner surface, although with an irregular shape locally. So, roughness details were added as a boundary condition for precision. Given a waveguide internal surface that was smooth, f(x,y) = 0, the power dissipation was P0, for a volume with x varying from x1 to x2, z varying from f(x) to g(x), and y varying from -8 to f(x,z), as determined by Eq. 7, where:
f(x) and g(x) = the upper and lower boundaries of the surface contour in the z direction, and a, b = waveguide width, height.
The added power dissipation for the whole waveguide due to surface roughness can be found by Eq. 8.
Numerical experiments were conducted to compare values from the proposed EC model and the traditional model with experimental data. For the purpose of the experiments, a seven-stage filter prototype was manufactured of H62 brass, plated with 10-m-thick silver and connected by a bolt (Fig. 2). The surface of the prototype filter's cavity was measured by means of the Taylor Hobson surface contour analyzer. The analyzer has a range of 200 μm and an accuracy (Ra = 0.1 μm and Rz = 0.1 μm). The local scanning pattern of the measurement report is shown in Fig. 3. Figure 4(a) shows an enlarged profile for a section of the surface roughness profile shown in Fig. 3, while Fig. 4(b) shows the same profile improved by digital filtering, in which the shortwave component, based on the operating frequency, is filtered out.
Although a 1D surface roughness model provides a clear understanding of the problem, it is more precise to treat a rough surface as a twodimensional (2D) model. Therefore, the rough surface was modeled by 2D fractal grooves of one unit length using the Matlab Version 7.1 mathematical software from The Math-Works. The basic model is shown in Fig. 5(a), with an improved version in Fig. 5(b) resulting from the removal of shortwave components based on operating frequency. The prototype is a seven-stage rectangular-waveguide filter centered at 14 GHz, with skin effect of 1.56 μm. The value of the shortwave components filtered out was 0.78 m.
A Monte-Carlo simulation was introduced for calculating average power dissipation.17,18 In these simulations, there were 8192 data points in each fractal rough surface, and each group contained 2000 rough surfaces. The dissipation ratio for every realization was calculated by solving Eq. 8 and computing average dissipation.
Figure 6 offers a comparison of experimental data with values determined by the proposed EC model (eq. 8), the EM model, and the mechanical model. The fractal model is the EM model. The exponential rough surface was taken as the first mechanical model and the Gaussian rough surface as the second one. These two kinds of rough surfaces were chosen to represent two modeling levels of realistic roughness, i.e., the former was rough in the long range but smooth in the short range, while the latter was rough evaluated over both short or long ranges.19, 20 Results of the EC model, the EM model, and mechanical model were obtained from a 2000-run Monte Carlo simulation; Matlab2009b was used for simulation. Experimental data from the prototypes in Fig. 2 were the reference. Results suggest the models show similar trends: for an increase in surface roughness, power dissipation also increases, with a maximum of 1.9 times that of the smooth inner surface in agreement with the literature.6,7
The RMS differences of the models were calculated separately, with a difference value of e for the exponential model found to be 0.035. The value of e for the fractal model was 0.0374 while the difference for the EC model was found to be 0.0233. The results from the EC model were found to be closer to the experimental results, indicating that it can more exactly describe the effects of the surface roughness than the other models.
To increase model applicability, a structured model was assembled in Fig. 7. This makes it possible to change parameters without limit. Based on the structured model, values for filter power dissipation at different frequencies are predicted in Fig. 8.
The table compares CPU times among four mathematical modes analyzing the rough surface of a rectangular waveguide with length of 15.8 cm, width of 7.04 cm, and height of 3.556 cm. The processing time for the Gaussian and exponential functions were similar, while the fractal function was about 10 times slower than the Gaussian and exponential functions due to the large amount of detailed information.8, 9 Although the fractal function was more efficient if limited to a computation of power loss, the EC model remains useful in the study of the electrical properties of irregularly shaped surfaces and structures. Compared with the two Monte Carlo models, the fractal approach took about four times more CPU time than the transverse electromagnetic (TE) approach for one surface realization, and about ten times more CPU time than the Gaussian and exponential functions. However, considering the large number of runs for convergence with a Monte Carlo simulation, the EC model was much faster than the original fractal function.
ACKNOWLEDGMENTS
This work was supported by the Fundamental Research Funds for the Central Universities (No. JY10000904019).
REFERENCES
1. N. Patir, Wear, Vol. 47, 1978, p. 263.
2. E. O. Hammerstad and F. Bekkadal, Editors, Microstrip Handbook, Trondheim, Norway, 1975.
3. L. Ponson, D. Bonamy, and E. Bouchaud, Physical Review Letters, Vol. 96, 2006, p. 3.
4. A. Majumdar and C.L. Tien, Wear, Vol. 136, 1990, p. 313.
5. A. Majumdar, and B. Bhushan, ASME Journal of Tribology, Vol. 112, 1990, p. 205.
6. S. P. Morgan, J. of Applied Physics, Vol. 20, 1949, p. 352.
7. C. L. Holloway and E. F. Kuester, IEEE Transactions on Microwave Theory & Techniques, Vol. 43, 2000, p. 2695.
8. K. Falconer, Ed., Fractal Geometry: Mathematical Foundations and Application, Wiley, New York, 1990.
9. B. B. Mandelbrot, Editor, The Fractal Geometry of Nature, Freeman, New York, 1983.
10. A. Majumdar, and B. Bhushan, ASME Journal of Tribology, Vol. 113, 1991, p. 1.
11. L. Proekt and A. C. Cangellaris, 53rd Proceedings of the International Conference on Electronic Components and Technology, 53rd, May 30, 2003, pp. 1004-1010.
12. T. Frederick, Editor, Radio Engineers' Handbook, McGraw-Hill, New York, 1943.
13. C. R. Paul, Editor, Introduction to Electromagnetic Compatibility, Wiley-InterScience, New York, 1992.
14. S. R. Seshadri, Editor, Fundamentals of Transmission Lines and Electromagnetic Fields, Addison-Wesley Educational Publishers, New York, 1971.
15. V. M. Papadopoulos, Quarterly Journal of Mechanics & Applied Mathematics, Vol. 7, 1954, p. 326.
16. Y. Konishi and K. Uenakada, IEEE Transactions on Microwave Theory & Techniques, Vol. 22, 1974, p. 869.
17. M. Kathryn Thompson, "Methods for Generating Rough Surfaces," in ANSYS, Proceedings of 2006 International ANSYS Conference, May 2-4, 2006; Pittsburgh, PA.
18. M. Q. Zou, B. M. Yu, Y. J. Feng, and P. Xu, Physica A, Vol. 386, 2007, p. 176.
19. J. A. Ogilvy and J. R. Fostert, Journal of Applied Physics, Vol. 22, 1989, p. 1243.
20. L. Tsang, X. Gu, and H. Braunisch, IEEE Microwave and Wireless Component Letters, Vol. 16, 2006, p. 221