Algorithms to Antenna: Understanding LFOV Arrays and Wideband Scanning Arrays

In a previous blog, we discussed the tradeoffs you should consider when building large phased arrays using smaller subarrays. Subarrays are utilized as building blocks for large arrays to save hardware costs by sharing transmit/receive (T/R) modules between multiple antenna elements. We have also blogged on the topic of modeling wideband systems, where wideband is defined as a system in which the spectral content in the signal is at least 10% of the carrier frequency.

In this latest installment, we talk about a topic where those two concepts intersect. We show how to model a subarray network with different configurations for two specific applications: limited-field-of-view (LFOV) arrays and wideband arrays.

Phased arrays provide high levels of flexibility in terms of the number of beams that can be formed and electronically steered. This flexibility does come with an implementation cost. Taking full advantage of a phased array requires placing steering circuitry and T/R switches behind each individual element. For applications that require large arrays with hundreds or thousands of elements, the cost of doing so may be too high to be practical. In addition, many applications don’t necessarily require a full degree of freedom from the array in terms of weighting control.

In practice, RF systems often employ a balanced approach. Elements are grouped into subarrays, and these subarrays are built up to form the larger array. The elements are still easy to manufacture; the entire array is still robust with respect to component failures. Moreover, T/R switches are only needed at each subarray, which helps to reduce system cost.

Limited-Field-of-View Arrays

An LFOV array only scans within a very limited window, normally less than 10 degrees. With the narrow steering range, subarrays can be used. They can be placed at a spacing much larger than half of the wavelength to help reduce the number of array elements in the system. When the spacing exceeds a value of half of the wavelength, we will see grating lobes. However, they will appear outside the narrow steering range and thus won’t impact performance in this type of application.

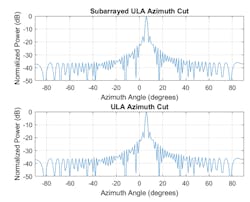
The simplest way to construct an array with subarrays is to contiguously tile the subarray. Figure 1 shows a 64-element uniform linear array (ULA) that consists of eight 8-element ULAs. Within each subarray, the elements are spaced by half the wavelength. There’s no steering capability inside each subarray, so the array can only be steered using subarrays.

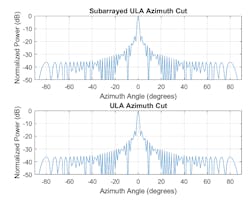
Figure 2 compares the radiation pattern of this array with the radiation pattern of a 64-element ULA with no subarrays.

From the plots, you can see that the two responses are identical when the beam is generated from the broadside of the array. This is true even when the subarrays are widely spaced apart.

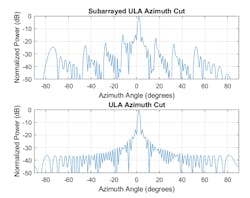
Let’s look at the same plots in Figure 3, when we steer both arrays to 2 degrees in azimuth.

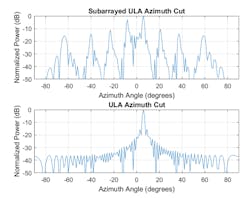
In this case, the response of our reference array still holds its original shape, but this isn’t the case for the subarrayed ULA. Note that although the mainlobe is correctly steered and stands well above the sidelobes, the response shows quantization lobes. The term was coined from the fact that the steering is at the subarray level and the required phase shift for each element is quantized at the subarray level. This effect become worse when the array is steered further from the broadside. Figure 4 shows the response after steering the arrays 6 degrees off broadside in azimuth. 

You can see how design tradeoffs need to be carefully considered when using contiguous arrays for an LFOV application.

One way to compensate for quantization lobes is to add phase shifters behind each element. Although it increases the system-level cost, it still delivers big savings when compared with having T/R switches at each element. Figure 5 shows the result with a phase shifter added to each element. As you can see, the response improves significantly for the 6-degree steering case.

As a side note, the element and the subarrays don’t necessarily steer to the same direction. In some applications, the elements inside the subarrays are steered toward a specific direction. The subarrays can then be steered to slightly different directions to search the vicinity.

Wideband Scanning Arrays

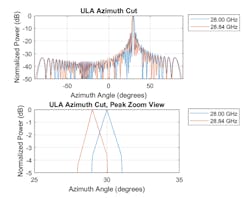
Although an electronically scanned array is often called a phased array, in reality, adjusting the phase is only one way to steer the array. The phase shifters are, by nature, narrowband devices. Consequently, they only work well within a narrow band, especially for large arrays. Figure 6 shows the radiation patterns when the reference array is phase steered to 30 degrees, both at the carrier frequency and at 3% above the carrier frequency.

Even though the frequency offset is only 3%, the peak location moved away from the desired direction of 30 degrees. This is referred to as squint effect. To achieve steering across a wideband signal, it’s better if you can steer the array using true time delays.

The most popular way to achieve a true time delay is to use cables. However, in a large array aperture with thousands of elements, implementing the potentially huge time delay may require lots of cables. This approach isn’t only expensive, it’s complex. Subarrays provide a compromise between the accuracy and feasibility.

The simplest way to realize this type of an array is to contiguously group the subarrays, as in previous sections.

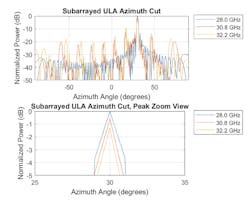
Figure 7 compares the radiation patterns at three frequencies for a subarrayed ULA. The array is steered toward 30 degrees azimuth at the subarray level using a true time delay. Again, within each subarray, the elements are also steered toward 30 degrees azimuth. The radiation pattern is shown at the carrier frequency, 10% above the carrier frequency, and 15% above the carrier frequency.

The plots reveal that the squint effect has been suppressed even though the bandwidth is much wider compared with the previous case. As we saw in the LFOV case, if the required bandwidth extends to 15% above the carrier frequency, the radiation pattern becomes undesirable due to quantization lobes.

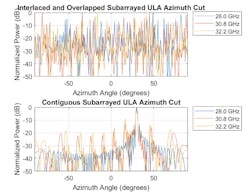
One way to address this issue is to use a configuration with aperiodic subarrays. Examples of these types of configurations are interlaced subarrays, overlapped subarrays, and even random subarrays.

In our final example, we use an interlaced subarray, where the ends of the subarray are interlaced and overlapped. Because it’s no longer formed by identical subarrays, we start with a large array aperture and partition it to achieve the overlapped configuration. The array geometry is shown in Figure 8.

The resulting radiation pattern from this type of array is illustrated in Figure 9.

You can see how the new radiation pattern suppresses the largest quantization lobe, achieving a gain of around 5 dB. Higher gains can be attained by designing a more sophisticated overlapped subarray network.

To learn more about the topics covered in this blog, see the examples below or email me at [email protected]:

• Direction of Arrival with Beamscan and MVDR with Simulink (documentation): Learn how to design and analyze phased arrays.
• Subarrays in Phased Array Antennas (example): Learn how to model subarrays, commonly used in modern phased-array systems.

See additional 5G, radar, and EW resources, including those referenced in previous blog posts.