Algorithms to Antenna: Clustered-Delay-Line Channel Model with Ray Tracing

What you'll learn:

What is a channel model, and what roles does a CDL play?
How is ray tracing used to configure the CDL channel model?
Steps in developing this framework for analyzing 5G urban settings.

In this blog, we build on an example described in a previous edition of the blog, where we showed how to analyze 5G urban scenarios using ray tracing. The premise is: “How can clustered-delay-line (CDL) channel model parameters, using the output of a ray-tracing analysis be customized?”

To start, we use ray tracing to calculate the geometric aspects of the channel including the number of rays, angles, delays, and attenuations. The results of the ray-tracing analysis can then be applied to configure the CDL channel model.

But first, a bit of background. A channel model is a representation of the channel that a transmitted signal follows to the receiver. A CDL is used to model the channel when the received signal consists of multiple delayed clusters—each cluster contains multipath components with the same delay but slight variations for angles of departure and arrival.

An example like the one described in this blog can be used to improve antenna-array designs and overall system-design parameters for 5G operations in dense urban settings. Our example includes a base station and a mobile device. The base station uses a rectangular array with 8 × 8 elements, and the mobile device uses a 2 × 2 rectangular array. Though it’s easy to customize for other designs, our system operates at 28 GHz with a 10-MHz bandwidth and subcarrier spacing of 15 kHz.

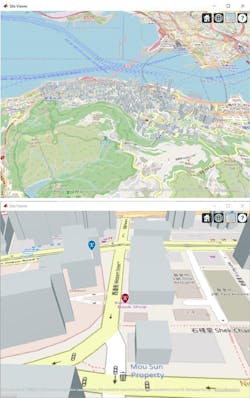
As we described in our earlier blog, we start by generating a .osm file for an urban setting in Hong Kong. The .osm file is downloaded from www.openstreetmap.org, which provides access to crowd-sourced map data all over the world.

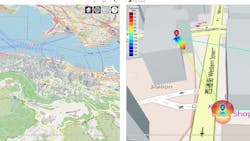
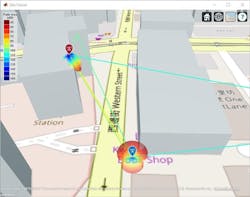
The left side of Figure 1 shows the dense urban environment in Hong Kong that we will evaluate, and the right side shows the base station (blue pin on top of the building) and the UE (red pin) on the map.

1. The top illustration shows a view of Hong Kong where the example is based. The bottom image is a zoomed-in view of the transmitter (blue) and user equipment (red).

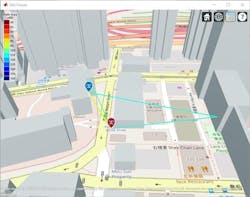
We perform ray-tracing analysis on this scene using the method of images. This method models surface specular reflections. Figure 2 shows four rays between the base station and the mobile device.

2. Propagation paths between the base station and the UE.

From the signal data generated by the ray tracing, we get the times of arrival, the average path gains, and the angles of departure and arrival. Our CDL channel model can be directly configured with the information generated by the ray-tracing analysis. Specifically, the ray tracer finds individual rays between the base station and the UE, while the CDL channel model identifies clusters of subrays whose properties are determined by the cluster average path gain, average angles of arrival and departure, and the spread of the rays in the cluster.

The ray tracer performs a static analysis, while the CDL channel models changes in propagation conditions, resulting in small-scale fading. Fading means that instantaneous channel path gains will differ from the average values, but over long simulations, their mean value will match the specified average path gains when using isotropic antennas.

The CDL channel also can model LOS components. For simplicity, this example assumes perfect channel estimation.

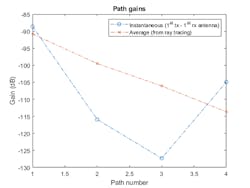
Figure 3 shows the instantaneous gains returned by the channel. Note how the results compare between the specified average path gains obtained from the ray attenuation values.

3. Path gains returned by the channel: instantaneous results vs. results obtained from ray tracing. (© 1984–2021 The MathWorks, Inc.)

The instantaneous path gains returned by the channel model include the gain of the antenna element in the direction of each ray. The custom path gains obtained from the ray-tracing analysis don’t include the antenna element gain. Therefore, in the mean, the channel-path gains match the average gains only for isotropic antenna elements.

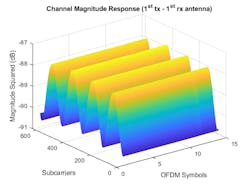
Figure 4 shows the channel response in time and frequency between the first transmit and the first receive antenna. This plot reveals a slight frequency selectivity of the channel.

4. Shown is the channel response in time and frequency between the first transmit and the first receive antenna. (© 1984–2021 The MathWorks, Inc.)

We also can calculate the beamforming weights using singular value decomposition (SVD). Figure 5 shows the radiation patterns obtained for the UE and the base station.

5. These are the radiation patterns obtained for the UE and the base station.

With this type of framework in place, other design parameters can be further explored. In addition to different urban settings, different antenna-array designs can be evaluated. For example, the 3GPP TR 38.901 includes a definition of a cross-polarized antenna, in addition to the array made up of subpanels. Figure 6 shows an example of a single subpanel and a 2 × 2 array of subpanels. These other designs can be used in the example to evaluate your design choices before you build a system.

6. Cross-polarization dipole, array configuration, and resulting array pattern using a cross-polarization antenna element for a single subpanel and a 2 × 2 array of subpanels. (© 1984–2021 The MathWorks, Inc.)

To learn more about the topics covered in this blog, see the examples below or email me at [email protected]:

Planning Radar Network Coverage over Terrain (example): Learn how to plan a radar network using propagation modeling over terrain.
SINR Map for a 5G Urban Macro-Cell Test Environment (example): Learn how to construct a 5G urban macro-cell test environment and visualize the signal-to-interference-plus-noise ratio (SINR) on a map.
5G Communications Systems (documentation): Learn how to simulate, analyze, and test 5G communications systems.