Algorithms to Antennas: Three-Dimension Indoor Positioning Using IEEE 802.11az Waveforms

This blog is part of the Algorithms to Antennas Series

What you'll learn:

• What is IEEE 802.11az?
• Using trilateration for positioning computations.
• Using deep learning to determine positioning.
  

This edition of Algorithms to Antennas describes an application in which RF signals are used to determine the position of an object. If you have been following this blog over the past four years, you might think radar is involved. While it’s a good guess since you can use radar to estimate an object’s position, we look instead to a wireless standard that supports positioning.

The IEEE 802.11az Wi-Fi standard defines the signals used to make measurements and the protocols employed to exchange timestamps. We will estimate the position of a station (STA) in a multipath environment using time-of-arrival (ToA) measurements. These measurements are fed into a multiple signal classification (MUSIC) algorithm to estimate the time of arrival of signals (super resolution beyond sample rate accuracy). We then estimate the two-dimensional position of a STA using trilateration.

Later in the post, we will use deep-learning techniques to predict the three-dimension position of STAs based on a fingerprint consisting of channel state information (CSI) measured at specific locations in an environment.

Positioning Using Trilateration

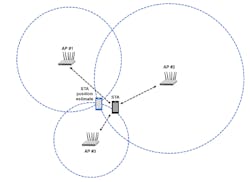
The IEEE 802.11az Wi-Fi standard is commonly referred to as next generation positioning (NGP). The standard provides physical-layer features that enable ranging and positioning. With this, we can use line-of-sight (LOS) conditions to extract temporal information, such as ToA, or spatial information such as angle of arrival (AoA), from a multipath signal to compute a distance between devices. When the range between at least three devices can be measured, trilateration may be used to compute a position estimate (Fig. 1).

The 802.11az standard enables a STA to identify its position relative to multiple access points (APs). For our first example, we create an 802.11az network that includes a STA and three APs. We simulate a ranging measurement exchange for each STA-AP pair. This allows us to perform trilateration to determine the position of the STA.

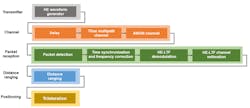
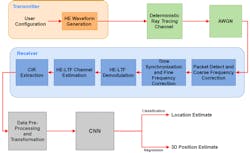
Figure 2 shows the steps performed in our simulation, from waveform generation to trilateration.

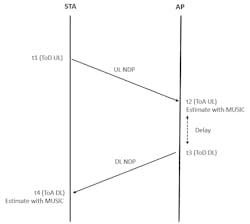
We calculate distance ranging measurements between the STA and each AP by capturing the timestamps of the null data packet (NDP). Figure 3 shows the measurement sounding phase between a STA and a single AP.

You can estimate TRTT, which is the roundtrip time (RTT), by combining the timestamps as follows:

TRTT = (t4 − t1) − (t3 − t2)

The distance (d) between the STA and AP by can then be calculated using this equation:

d = TRTT c/2

where c is speed of light, and t2 and t4 are estimated using the MUSIC algorithm.

Figure 4 shows the ranging process that’s performed.

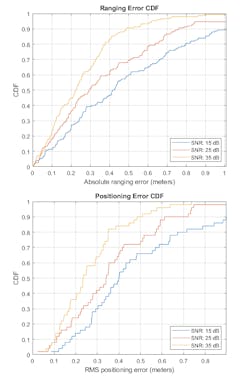
The AP and the STA exchange multiple uplink and downlink packets. We run this analysis over multiple iterations to ensure robustness of the results. For each iteration, we use a different random set of AP positions, a different channel realization, and a different AWGN profile. The results are used to generate a cumulative distribution function (CDF) for the absolute ranging error by applying the ranging measurements from all iterations and all STA-AP pairs.

The ranging mean absolute error (MAE) for three SNR values are as follows:

The average RMSE for each SNR point are as follows:

Figure 5 shows both the ranging error CDF (top) and the positioning error CDF (bottom).

Note that the results are better in terms of smaller errors for range and positioning as the SNR increases, as expected.

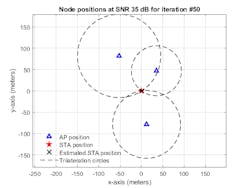
Figure 6 shows the location estimate and the trilateration circles of a single iteration. As can be seen, the estimated position is close to the ground truth.

Positioning Using Deep-Learning Techniques

Let’s look at a similar example, but this time we will train a convolutional neural network (CNN) to localize and estimate STA positions with IEEE 802.11az data. The trained network makes estimates based on a fingerprint consisting of multiple channel impulse responses (CIRs).

Fingerprinting and deep-learning techniques can be used in Wi-Fi positioning systems to achieve sub-meter accuracies even in non-line-of-sight (NLOS) multipath environments. A fingerprint typically contains channel state information, such as a received signal strength indicator (RSSI) or a channel estimate from a received signal, measured at a specific location in an environment.

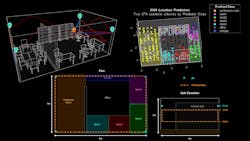
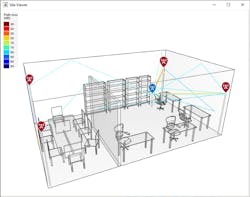
We synthesize a dataset of CIR fingerprints by using 802.11az signals in an indoor environment and label each fingerprint with its location information. Figure 7 shows our indoor environment, including four APs and a number of STAs. The red square markers (Figure 7, bottom) indicate the locations of the APs. The blue dashed box (Figure 7, bottom right) represents the area where we distribute STAs during the training process.

We restrict the height of the STAs to a range between 0.8 and 1.8 meters to ensure a realistic set of values for portable consumer devices. This constraint also minimizes the chance of STAs being placed in unreachable positions.

We simulate fingerprints based on the propagation channel defined by the environment along with the associated CIR obtained using ray-tracing techniques.

The trained network can be configured to perform localization or positioning. Localization is a classification task where the output of the model is a predicted label related to a discrete area of the map where a STA is located. Localization is useful when precise positioning is less important than being able to estimate the general location of a user with a high degree of accuracy—for example, a room on the floor of a building or an aisle in a store.

Positioning is a regression task in which the output of the model is the predicted position of a STA. Positioning can estimate the exact location of the user, but it may have a higher error for positions across an area when compared to localization.

Figure 8 shows the calculated rays between all APs and a single STA for a specific configuration. The color of the rays represents the associated path loss in dB.

As shown in Figure 9, each AP transmits an 802.11az packet through a noisy channel, and each STA receives the packet. To simplify our example, we assume each STA can differentiate between APs, and that no interference occurs between APs. To simulate variations in the environment, the fingerprinting process is repeated for a range of SNR values (10, 15, and 20 dB).

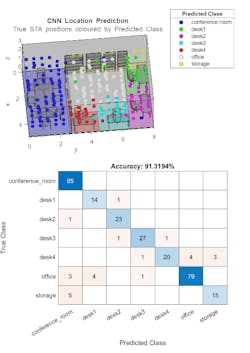
For localization, Figure 10 (top) shows a three-dimensional map, which displays the true locations of STAs. The color assigned to each STA denotes its predicted location. Figure 10 (bottom) depicts a confusion matrix in which the rows correspond to the predicted class and the columns correspond to the true class. The diagonal cells correspond to observations that are correctly classified. The off-diagonal cells correspond to incorrectly classified observations. If the network performs well, elements in the main diagonal are significantly larger than the other matrix elements.

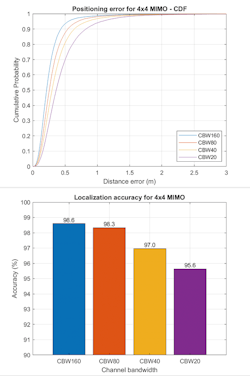
It’s important to note that both the channel bandwidth and the size of the transmit and receive antenna arrays control the quantity of data and its resolution within each fingerprint. This means larger antenna arrays produce more channel realizations and more CIRs per fingerprint. A higher bandwidth increases the sample rate of the CIR, capturing it in more detail.

Figure 11 shows the impact of channel bandwidth on positioning and localization performance. As expected, using a larger channel bandwidth results in more accurate estimation, since higher sampling rates increase the resolution of CIRs.

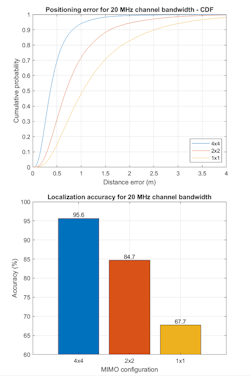
Figure 12 shows the impact of the number of transmit and receive antennas. These results were generated using a bandwidth of 20 MHz. The accuracy increases for larger antenna arrays due to the presence of more channel information. For example, a 4×4 channel contains 16 channel realizations, whereas a 2×2 channel contains only four. As expected, the CNN performs better when trained with more data.

To learn more about the topics covered in this blog and explore your own designs, see the examples below or email me at [email protected]:

• 802.11az Positioning Using Super-Resolution Time of Arrival Estimation (Example): Learn how to estimate the position of a station in a multipath environment by using a time-of-arrival-based positioning algorithm defined in the IEEE 802.11az Wi-Fi standard.
• Three-Dimensional Indoor Positioning with 802.11az Fingerprinting and Deep Learning (Example): Learn how to train a convolutional neural network for localization and positioning by using generated IEEE 802.11az data.
• Design a Deep Neural Network with Simulated Data to Detect WLAN Router Impersonation (Example): Learn to design a radio frequency fingerprinting a convolutional neural network with simulated data.

See additional 5G, radar, and EW resources, including those referenced in previous blog posts.

Rick Gentile is Product Manager, Colin McGuire is Senior Team Lead, Faisal Darbari is a Software Engineer, and Honglei Chen is Principal Engineer at MathWorks.

Read more blogs in the Algorithms to Antennas Series