Algorithms to Antenna: Increasing Angular Resolution Using MIMO Radar
Radars with multiple-input, multiple-output (MIMO) waveforms can be used to increase angular resolution. The goal is to use a smaller-form-factor phased-array antenna that transmits MIMO waveforms and receives these waveforms with fewer receive elements. MIMO waveforms make it possible to form a virtual array. The virtual array generates a more focused beam pattern as though it was generated from a much larger array. This technique is popular in automotive radar space, where smaller form factors are critical.
A virtual array can be created by quasi-monostatic MIMO radars, in which the transmit and receive arrays are closely located. The two-way pattern of a phased-array radar is the product of its transmit-array pattern and receive-array pattern.
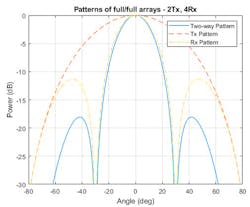
Let’s consider a millimeter-wave (mmWave) radar with a two-element transmit array and a four-element receive array. If both arrays have half-wavelength spacing, the two-way pattern is close to the receive array pattern (Fig. 1).
1. Shown is a pattern for two-Tx and four-Rx array with half wavelength spacing.
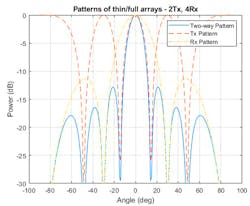
If the transmit-array elements increase in spacing (wider than half wavelength), the two-way pattern has a narrower beamwidth. Figure 2 shows that even though the transmit array has grating lobes, the grating lobes are not present in the two-way pattern.
2. The pattern for two-Tx (with wider than half wavelength spacing) and four-Rx array (half wavelength spacing) is depicted.
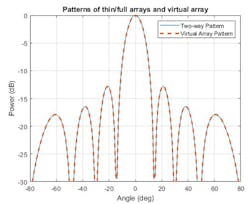
The two-way pattern of this system corresponds to the pattern of a virtual receive array with 2 × 4 = 8 elements. If you carefully choose the geometry of the transmit and the receive arrays (Fig. 3), the angular resolution of the system increases without adding more antennas to the arrays (Fig. 4).
3. Here’s the geometry of transmit array (2λ spacing) and receive array to generate a two-way pattern.
4. Two-way pattern versus pattern from virtual array is plotted.
Coherent MIMO radar antenna arrays can transmit orthogonal waveforms. With this orthogonality, it’s possible to recover each transmitted signal at the receive array. The measurements at the receive array corresponding to each orthogonal waveform can then be stacked to form the measurements of the virtual array (Fig. 5).
5. Geometry of transmit array (2λ spacing) and receive array using orthogonal waveforms is shown.
In this case, if each element in the transmit array radiates independently, there’s no transmit beamforming. The result is that the transmit pattern is broad. This allows for the simultaneous illumination of all targets over a broad view. The receive array can generate multiple beams to process all target echoes. Compared with conventional phased-array radars that need successive scans to cover the entire field of view, this is another advantage of MIMO radars for applications that require fast reaction time.
TDM-MIMO Radar
Time-division-multiplexing (TDM) waveforms can be used to achieve orthogonality among transmit channels. I have a model of this system and was able to try out the algorithm on a commercially available hardware platform, the Demorad 24-GHz radar sensor platform from Analog Devices.
Following the story from above, the system modeled has two transmitters separated by 1.5 times the wavelength. There are four physical receive elements. The goal is to compare the angular resolution with a four-element Rx array and a virtual array of seven elements (Fig. 6).
6. In this figure, geometry of transmit array (1.5λ spacing) and receive array is depicted.
For the non-MIMO simulation and measurements, a single Tx element is used to create a broad transmit beam for each pulse repetition interval (PRI). With a four-element receive array, the receive beam width is approximately 30 degrees. If the objects in the field of view are within the 30-degree beam, it will be difficult to resolve that there are two objects.
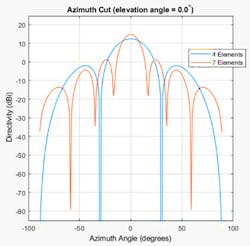
MIMO operations were then implemented using alternating pulses in time (Tx pulse 1 and Tx pulse 2) from the spatially separate transmit elements. The goal was to achieve improved angular resolution (approximately 17 degrees) over the non-MIMO operations case. Figure 7 shows the comparison of the two beam patterns for this scenario. The narrow beam will give more angular resolution as it’s scanned through the field of view.
7. This is a beam-pattern comparison of four-element physical array (blue line) and seven-element virtual array (red line).
Figure 8 is a photo of the array.
8. Shown is a phased-array antenna for a 24-GHz system (two Tx and four Rx).
In this scenario, we modeled two objects separated by 25 degrees (Fig. 9). With a larger beam (non-MIMO), the two objects look like a single return. With the virtual array created by using MIMO, a narrow beam helps to resolve the two objects.
9. Comparing live data versus simulation.
In addition to the model, we are able to perform the same measurements using the hardware in MIMO and non-MIMO mode. Figure 9 also shows the results when my colleague and I are the closely separated objects. Here, instead of synthesizing the scene, we were part of the scene. The data was brought into MATLAB as it was generated, and the baseband processing was done in Phased Array System Toolbox.
The results confirm that the simulation and measured data agree. The objects in the scene are separated by 25 degrees and located at the same range. In the MIMO case (measured and simulated), two targets are resolved. In the non-MIMO case, the two targets appear as a single object.
To learn more about the topics covered in this blog, see the links below or email me at [email protected].
- Increasing Angular Resolution with MIMO Radars (example): Learn how forming a virtual array in MIMO radars can help increase angular resolution. Understand how to simulate a coherent MIMO radar signal processing chain.
- MIMO Wireless System Design for 5G, LTE, and WLAN in MATLAB (webinar): Learn how to use MATLAB for modern wireless design.
- Phased Array System Toolbox (overview): Learn about the algorithms and apps in Phased Array System Toolbox for the design, simulation, and analysis of sensor array systems in radar, wireless-communication, EW, sonar, and medical-imaging applications.
See additional 5G, radar, and EW resources, including those referenced in previous blog posts.
About the Author
Rick Gentile
Product Manager, Phased Array System Toolbox and Signal Processing Toolbox
Rick Gentile is the product manager for Phased Array System Toolbox and Signal Processing Toolbox at MathWorks. Prior to joining MathWorks, Rick was a radar systems engineer at MITRE and MIT Lincoln Laboratory, where he worked on the development of several large radar systems. Rick also was a DSP applications engineer at Analog Devices, where he led embedded processor and system level architecture definitions for high performance signal processing systems used in a wide range of applications.
He received a BS in electrical and computer engineering from the University of Massachusetts, Amherst, and an MS in electrical and computer engineering from Northeastern University, where his focus areas of study included microwave engineering, communications, and signal processing.