Download this article as a .PDF
A high-impedance tunable composite right/left-handed (CRLH) coplanar-waveguide (CPW) transformer provides an effective means of matching a 200-Ω load to a 50-Ω line. By applying DC magnetic bias, it is possible to tune the bandwidth of the transformer, with the center frequency changing from 2.8 to 3.4 GHz.
With a length of 2.4 mm, this transformer represents about a 78% reduction compared to a conventional transformer in the same frequency band. The CRLH transformer’s CPW configuration employs a horizontally magnetized ferrite substrate with small demagnetization field so that very little DC magnetic bias is needed for tuning compared to microstrip configurations.
Composite right/left-handed (CRLH) transmission lines (TLs) have been proposed as a form of transmission line with novel properties.1-4 These TLs have been shown to have effective negative dielectric permittivity and magnetic permeability. The CRLH TLs have been incorporated in many compact, multiband microwave components (phase shifters, power dividers, filters, oscillators, and antennas).16-21 From these components, microwave impedance transformers based on CRLH TLs have been developed, characterized by small size and wide bandwidth.5,6
A need for tunable and nonreciprocal microwave devices and antennas has encouraged researchers to create tunable and nonreciprocal CRLH TLs using ferrite substrates.22-26 A ferrite medium has nonreciprocal dispersive properties due to its dispersive permeability tensor.27 The tuning characteristics are achieved by varying the applied DC magnetic bias.
Over the ferrite CRLH TLs, it has proven that CPW-based devices require less DC magnetic bias compared to microstrip configuration.22 Examples of these devices include tunable/nonreciprocal couplers, resonators, circulators, phase shifters,28-41 and antennas.42,43
Ferrite CRLH TLs can be designed by periodically loading a hosting planar ferrite TL by a shunt inductive load, LL, and a series capacitive load, CL. The shunt inductive load yields negative effective permittivity, while series capacitive load results in negative effective permeability. Analysis of a ferrite CRLH TL can be performed in a manner similar to that for a CRLH TL based on dielectric substrate, using either periodic circuit analysis or CRLH analysis.
For simplicity in both analysis methods, the ferrite TL will be expressed in terms of its medium parameters. The propagation constant along the hosting ferrite TL and its characteristic impedance can be expressed in terms of the permittivity and permeability of its medium as44:
k = ω(μ0μfε0εf)0.5 (1)
Z0 = (μ0μf /ε0εf)0.5 (2)
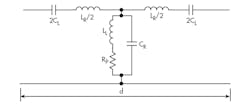
where m0 and e0 are the free space permeability and permittivity, respectively, while ef is the relative ferrite permittivity and mf is the equivalent relative ferrite permeability of the hosting TL, which changes according to the direction of the applied DC magnetic field. The equivalent circuit of a lossless ferrite CRLH TL unit cell of length (d) can be expressed using a standard lossless CRLH unit cell (Fig. 1).
In the equivalent-circuit model, the parasitic inductance (LR) and capacitance (CR) of the hosting ferrite TL substrate are calculated in terms of the ferrite medium permittivity and the equivalent relative ferrite permeability, which depends of the direction of the applied DC magnetic bias. For periodic analysis of a ferrite CRLH TL with (a) properly defined equivalent relative permeability of the hosting ferrite TL according to the direction of the DC magnetic bias, and (b) the periodic length of the unit cells (d) being very small compared to the propagating wavelength hence, the dispersion equation can be written as:44
cos(βd) = 1 – 0.5ω2d2(μ0μf – 1/ω2CLd)(ε0εf – 1/ω2LLd) (3)
where b denotes the complex propagation constant of the travelling wave along the periodic structure.
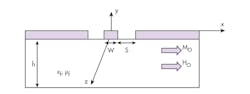
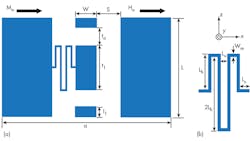
Figure 2 shows a front view of the three-dimensional (3D) geometry of the proposed CPW ferrite CRLH transformer, with a layout of the transformer in Fig. 3a. The CRLH LH unit cell consists of a CPW section loaded by two series air gap capacitor and a meandered line inductor (Fig. 3b) and fed by CPW TLs at the ends.
An internal DC magnetic field (H0) is applied to the ferrite substrate, producing the saturation magnetization in the direction shown. The progressive phase shift and the characteristic impedance of a CRLH TL unit cell, of length d, implemented on a ferrite substrate, can be redefined approximately in terms of its medium parameters, the ferrite relative permittivity εf, and the relative permeability μf (as illustrated in ref. 44):
ϕCRLH = ωd [(μ0μf – 1/ω2CLd) )(ε0εf – 1/ω2LLd)]0.5 (4)
ZCLRH = ZL[(1 – ω2 μ0μfCLd)/(1 – ω2ε0εfLLd)]0.5 (5)
Because of the dispersive nature of the ferrite substrate, the ferrite TL has a dispersive permeability such that the progressive phase shift and the CRLH characteristic impedance are dispersive.
The ferrite CRLH transformer makes use of these dispersive, progressive phase shifts and characteristic impedance so that their combination always meets the impedance-matching condition. The transformer does not behave like a typical quarter-wave transformer. The electrical length, ϕCRLH , will no longer be 90 deg. as the DC bias varies, and the characteristic impedance, ZCRLH , will also change. But, the overall effect of these changes is that the input impedance, Zin, will be almost constant for its desired value, forming a tunable transformer.
The initial design of the CRLH transformer was based on considering the ferrite substrate as an isotropic material. This can be done by assuming a very high DC magnetic bias applied to the ferrite substrate (H0 = 50,000 Oe ). At this bias, the onset frequency of the negative permeability is shifted to greater than 60 GHz, which is much higher than the target design frequency band.44 Therefore, the ferrite substrate for the frequency bands of interest can be characterized as an isotropic material.
Hence, the ferrite substrate can be characterized only with its electric properties within the transformer operating frequency. Under this condition, the ferrite CRLH transformer was designed to match a 200-W load (Zload) to a 50-W TL (Zol) at 3.45 GHz. Accordingly, the CRLH transformer should have 100-W characteristic impedance (ZLH), [ZLH = (Zol Zload)0.5], and +90-deg. phase shift at its output terminal.
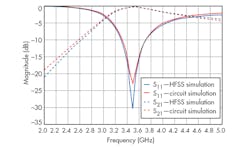
These two conditions were fulfilled by the proper selection of both loading and hosting CPW TL elements. Comparison of the two simulation results is shown in Fig. 4, where good agreement of both simulations is apparent.
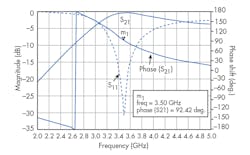
The phase shift of the ferrite CRLH transformer, achieved by applying a high DC magnetic bias of H0 = 50,000 Oe, is shown in Fig. 5. The transformer exhibits almost 90-deg. phase shift in the LH passband at 3.5 GHz. Figure 5 also shows the return and transmission losses of the transformer terminated with a 200-W load. It is evident that the transformer has minimum return loss better than 25 dB and close to 0-dB insertion loss at 3.5 GHz. Also, it has a 3-dB bandwidth from 3.05 to 4.4 GHz (36%).
The CRLH transformer is tuned by varying the applied DC magnetic bias. Because of the magnetization of the ferrite material, the internal magnetic field (H0) is different than the external magnetic field (Hex). The relationship between the two magnetic fields can be expressed as44:
Hex = H0 + 4πMSN (6)
where N is the demagnetization factor for the applied DC magnetic bias direction. The demagnetization factor depends on the geometry of the ferrite material. As explained in ref. 44, the demagnetization factor is almost 1 if the DC bias direction is perpendicular to the plane of a rectangular ferrite specimen, while it is almost zero if the DC magnetic bias is in plane. Therefore, for a CPW structure, the in-plane demagnetization field for the shown applied field direction in Fig. 1 has little effect.
However, for improved accuracy, the current study compensates for the external applied DC magnetic bias. Accordingly, a uniform demagnetization filed was calculated to be equal to 70 Oe, which represents the difference between the external and internal DC magnetic fields.
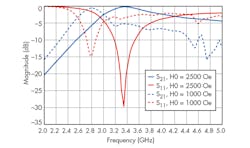
To illustrate the CRLH transformer’s tuning capability, two more lower DC magnetic bias cases of 1,000 Oe and 3,000 Oe were numerically studied (Fig. 6). It is clear that the operating frequency of the CRLH transformer can be tuned from 2.8 GHz in the first case to 3.35 GHz in the second case with better than 15-dB return loss and about 0.5-dB insertion loss in both cases. The operating bandwidth is tuned from 2.55 to 3.1 GHz (20%) in the first case and 2.95 to 4.2 GHz (35%) in the second case.
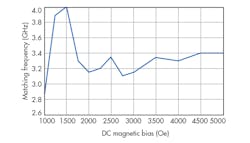
By increasing the DC bias further, the transformer tenability becomes even more apparent. Figure 7 shows change of center frequency versus DC bias. The transformer center frequency exhibits nonlinear variation with the applied DC magnetic bias. It increases from 2.8 GHz at H0 = 1,000 Oe to 4 GHz at H0 = 1,500 Oe and decreasing to 3.05 GHz at 2,000 Oe. This increase/decrease process then repeats two times with small frequency variations steps. Finally, the matching frequency reaches 3.4 GHz at 4,500 Oe and remains constant to 5,000 Oe.
The nonlinear variation of the center frequency, and specifically its drop at H0 = 2000 Oe, can be explained as due to the nonlinear variation of the hosting ferrite TL permeability versus frequency. By emphasizing its change in value versus frequency, it can be seen that its value increases from 1 and then decreases to negative values within the frequency band of negative ferrite permeability, before finally returning to unity beyond this frequency band. As a consequence, this nonlinear variation is expected to affect both the progressive phase shift and the characteristic impedance of a CRLH TL unit cell (defined in eqs. 4 and 5, respectively).
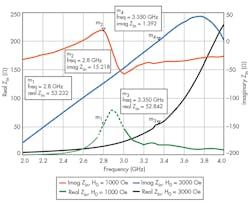
Verification of the theoretical concept of an CRLH transformer can be done by studying the input impedance for different DC magnetic bias values. For these two studied cases of H0, the input impedance of the CRLH transformer was calculated numerically (Fig. 8). These calculations show that the input impedance is Zin= 53.232 + j15.218 Ω at 2.8 GHz for H0 = 1000 Oe. This changes to Zin= 52.842 + j1.392 Ω at 3.55 GHz for H0 = 3000 Oe. It is clear that the CRLH transformer demonstrates close to 50-Ω input impedance at two different frequencies.
Mahmoud A. Abdalla, Associate Professor
Military Technical College, Cairo, Egypt
Zihrun Hu, Senior Lecturer
School of Electronics and Electrical Engineering, University of Manchester, P.O. Box 88, Manchester M60 1QD, UK
References
1. C. Caloz and T. Itoh, Electromagnetic Metamaterials Transmission Line Theory and Microwave Applications, 1st ed., Wiley, New York, 2006.
2. H-X. Xu, G-M. Wang, C-X. Zhang, and X. Wang. “Characterization of composite right/left-handed transmission line,” Electronics Letters, Vol. 47, No. 18, 2011, pp. 1,030-1,032.
3. Q. Yang, and Y. Zhang. “Non-radiative composite right/left-handed transmission line based on ridge substrate integrated waveguide,” Electronics Letters, Vol. 49, No. 20, 2013, pp. 1,280-1,282.
4. Q. Shen, “Simple broadband via-free microstrip composite right and left hand transmission line,” Electronics Letters, Vol. 52, No. 9, 2016, pp. 724-725.
5. C. Damm, J. Freese, M. Schubler, and R. Jakoby. “Electrically controllable artificial transmission line transformer for matching purposes,” IEEE Transactions on Microwave Theory & Techniques, Vol. 55, No. 6, 2007, pp. 1,348-1,354.
6. A.F. Daw, M.A. Abdalla, and H.M. Elhennawy, “New Inductor Loaded Composite Right Left hand Impedance Transformer for UWB Wireless Applications,” 2015 9th International Congress on Advanced Electromagnetic Material in Microwave and Optics, 2015, United Kingdom, pp. 231-233.
7. S.C. Wenjing Su, Manos, M. Tentzeris, and S. Lim. “A novel fluid-reconfigurable advanced and delayed phase line using inkjet-printed microfluidic composite right/left-handed transmission line,” IEEE Microwave and Wireless Components Letters, Vol. 25, No. 2, 2015, pp. 142-144.
8. H-X. Xu, G-M. Wang, and X. Wang. “Compact Butler matrix using composite right/left handed transmission line,” Electronics Letters, Vol. 47, No. 19, 2011, pp. 1,081-1,083.
9. M. Bemani, and S. Nikmehr, “Nonradiating arbitrary dual-band equal and unequal 1: 4 series power dividers based on CRLH-TL structures,” IEEE Transactions on Industrial Electronics, Vol. 61, No. 3, 2014, pp. 1,223-1,234.
10. X. Ren, K. Song, M. Fan, Y. Zhu, and B. Hu. “Compact dual-band Gysel power divider based on composite right-and left-handed transmission lines,” IEEE Microwave and Wireless Components Letters, Vol. 25, No. 2, 2015, pp. 82-84.
11. H-X. Xu, G. M. Wang, X. Chen, and T. P. Li. “Broadband balun using fully artificial fractal-shaped composite right/left handed transmission line,” IEEE Microwave and Wireless Components Letters, Vol. 22, No. 1, 2012, pp. 16-18.
12. Y. Peng, X. Peng Yu, J.M. Gu, W.M. Lim, and W.Q. Sui, “An area-efficient CRLH (Composite Right/Left-Handed)-TL approach to the design of rotary traveling-wave oscillator,” IEEE Microwave and Wireless Components Letters, Vol. 23, No. 10, 2013, pp. 560-562.
13. K. Song, Q. Duan, F. Chen, B. Hu, and Y. Fan, “Design of dual-bandpass filter using zeroth-order resonance and Bragg frequency,” IET Microwaves, Antennas & Propagation, Vol. 9, No. 5, 2014, pp. 431-435.
14. M.A. Abdalla and K.S. Mahmoud, “A Compact SIW Metamaterial Coupled Gap Zeroth Order Bandpass Filter with Two Transmission Zeros,” 2016 10th International Congress on Advanced Electromagnetic Material in Microwave and Optics, 2016, Greece, pp. 4-6.
15. M. Abdalla, A. Hassan, and A. Galal Eldin, “A Compact High Selective Coupled Gap CRLH TL Based Bandpass Filter,” 2015 9th International Congress on Advanced Electromagnetic Material in Microwave and Optics, 2015, United Kingdom, pp. 237-239.
16. L. Li, Z. Jia, F. Huo, and W. Han, “A novel compact multiband antenna employing dual-band CRLH-TL for smart mobile phone application,” IEEE Antennas and Wireless Propagation Letters, Vol. 12, 2013, pp. 1688-1691.
17. Y. Kushiyama, T. Arima, and T. Uno, “Differential-Type CRLH Leaky-Wave Antenna Using Stepped Impedance Resonators,” IEEE Antennas & Wireless Propagation Letters, Vol. 15, 2016, pp. 321-324.
18. M.A. Abdalla, U. Abdelnaby, and A.A. Mitkees, “Compact and Triple Band Metamaterial Antenna for All WiMAX Applications,” 2012 International Symposium on Antennas and Propagation, pp. 1,176-1179.
19. Mahmoud Abdalla, “A Dual Mode CRLH TL Metamaterial Antenna,” 2014 IEEE AP-S International Antenna and Propagation Symposium Digest, 2014, pp. 793-794.
20. M. Abdalla, M. Abo El-Dahab, and M. Ghouz, “Dual/Triple Band Printed Dipole Antenna Loaded With CRLH Cells,” 2014 IEEE AP-S International Antennas & Propagation Symposium, pp. 1,007-1,008.
21. M.A. Abdalla, A.A. Awad, and K.M. Hassan, “Wide Band High Selective Compact Metamaterial Antenna for 2 GHz Wireless Applications,” 2014 Loughborough Antennas & Propagation Conference, 2014, United Kingdom, pp 350-354.
22. M. Tsutsumi and T. Ueda, “Nonreciprocal left-handed microstrip lines using ferrite substrate,” in Proceedings of the IEEE MTT-S International Symposium, 2004, pp. 249-253.
23. M. Tsutsumi and T. Ueda, “Left handed transmission characteristics of ferrite microstrip lines without series capacitive load,” IEICE Transactions on Electronics, Vol. E89, September 2006, pp. 1,318-1,323.
24. M. Abdalla and Z. Hu, “On the study of CWP dual band left handed propagation with reciprocal and nonreciprocal characteristics over ferrite substrates,” in IEEE AP-S International Symposium, 2007, pp. 2,578-2,581.
25. G. Sajin, I. A. Mocanu, F. Craciunoiu, and M. Carp, “MM-wave left-handed transmission line antenna on anisotropic substrate,” 43rd European Microwave Conference (EuMC), 2013, pp. 668-671.
26. Y.-J Huang, G. Wen, T. Q. Li, Li, and J. L. Kang Xie, “Design and Characterization of Tunable Terahertz Metamaterials With Broad Bandwidth and Low Loss,” IEEE Antennas and Wireless Propagation Letters, Vol. 11, 2012, pp. 264-267.
27. B. Lax and K. J. Button, Microwave Ferrites and Ferrimagnetics, McGraw-Hill, New York, 1962.
28. M.A. Abdalla and Z. Hu, “Multi-band functional tunable LH impedance transformer,” Journal of Electromagnetic Wave and Applications, Vol. 23, 2009, pp. 39-47.
29. M.A. Abdalla and Z. Hu, “Compact tunable left handed ferrite transformer,” International Journal of Infrared and Millimeter Waves, Vol. 30, No. 8, 2009, pp. 813-825.
30. M. Abdalla and Z. Hu, “Compact Novel CPW Ferrite Coupled Line Circulator with Left-handed Power Divider/Combiner,” 2011 European Microwave Week (EuMW) Digest, United Kingdom, pp. 794-797.
31. T. Kodera, and C. Caloz, “Integrated Leaky-Wave Antenna–Duplexer/Diplexer Using CRLH Uniform Ferrite-Loaded Open Waveguide,” IEEE Transactions on Antennas and Propagation, Vol. 58, No. 8, 2010, pp. 2,508-2,514.
32. T. Kodera, D.L. Sounas, and C. Caloz, “Tunable magnet-less non-reciprocal metamaterial (MNM) and its application to an isolator,” 2012 Asia-Pacific Microwave Conference (APMC) Proceedings, pp. 73-75.
33. M. Abdalla and Z. Hu, “Ferrite Tunable Metamaterial Phase Shifter,” 2010 IEEE AP-S International Antenna and Propagation Symposium Digest, July 11-17, 2010, Toronto, Canada, pp. 1-4.
34. M. Tsutsumi and K. Okubo, “Effect of stubs on ferrite microstrip line magnetized to wave propagation,” Asia Pacific Microwave Conference 2009 (APMC 2009), pp. 1,234-1,237
35. M.A. Abdalla and Z. Hu, “Compact tunable single and dual mode ferrite left-handed coplanar waveguide coupled line couplers,” IET Microwaves, Antennas & Propagation, Vol. 3, No. 4, June 2009, pp. 695-702.
36. M. Abdalla and Z. Hu, “Composite Right/Left-handed Coplanar Waveguide Ferrite Forward Coupled-Line Coupler,” IET Microwaves, Antennas & Propagation, Vol. 9, No. 10, 2015, pp. 1,104-1,111.
37. S. Karimian, M. Abdalla, and Z. Hu, “Tunable Metamaterial Ferrite Stepped Impedance Resonator (SIR),” 27th Progress in Electromagnetics Research Symposium, 2010, Xi’an, China, pp 165-168.
38. M.A. Abdalla and Z. Hu, “Compact Metamaterial Coplanar Waveguide Ferrite Tunable Resonator,” IET Microwaves, Antennas & Propagation, Vol. 10, No. 4, 2016, pp. 406-412.
39. M. Abdalla and Z. Hu, “Design and Analysis of Tunable Left Handed Zeroth Order Resonator on Ferrite Substrate,” IEEE Transactions on Magnetics, Vol. 44, November 2008, pp. 3,095-3,098.
40. J. Ghalibafan and Nader Komjani, “Tunable zeroth-order resonator based on a ferrite metamaterial structure,” Chinese Physics B, Vol. 22, No. 10, 2013, pp. 107805-1-107805-5.
41. A. Zermane, B. Sauviac, B. Bayard, B.P. Gervy, J.J. Rousseau, and A. Benghalia, “Experimental verification of tunable property of a zeroth-order resonator on ferrite substrate,” Microwave and Optical Technology Letters, Vol. 56, No. 12, 2014, pp. 2,805-2,809.
42. M. Abdalla and Z. Hu, “Compact and Tunable Metamaterial Antenna for Multi-band Wireless Communication applications,” 2011 IEEE AP-S International Antennas & Propagation Symposium USA, pp. 2,951-2,953.
43. A. Porokhnyuk, T. Ueda, Y. Kado, and T. Itoh, “Design of nonreciprocal CRLH metamaterial for non-squinting leaky-wave antenna,” 2013 IEEE MTT-S Intenational Microwave Symposium (IMS), pp. 1-3.
44. Mahmoud Abdelrahman Abdalla, “Ferrite left-handed meta-materials for RF microwave applications,” Ph.D. dissertation, Manchester University, Manchester, UK, 2008.