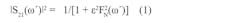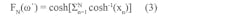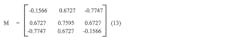Download this article in PDF format.
Microwave bandpass filters (BPFs) are essential for maintaining separate channels in wireless communications systems. As such systems become more compact, BPFs must meet more demanding requirements for smaller size, lower insertion loss, higher out-of-band rejection (selectivity), and lower cost. Several techniques are used to design microwave BPFs,1-4 although the authors have developed an approach that delivers BPFs with extremely low passband insertion loss in smaller-than-conventional sizes. The secret lies in the use of metamaterials.
The cutoff points for the rejection bands of a BPF are located by attenuation poles or transmission zeros at finite frequencies. This can be done with different design approaches. For example, cross-coupling between nonadjacent resonators allows for creation of alternative signal paths from filter input to output ports, so that a complete transmission zero can be introduced at certain frequencies.4-10 Hence, many filter designs incorporate transmission-line zeros.11-13
Another important choice in the design of a filter regards the physical elements, which will impact the filter response and size. Open-loop resonators have often been used in microwave filter design.14-18 The open-loop resonator is constructed by adding half-wave-length microstrip lines with a certain coupling structure to achieve the required filter performance. Three types of coupling methods are used in these filters: electric coupling, magnetic coupling, and mixed coupling.19-21
For microstrip open-loop resonator filters, several attempts have been made to reduce the resonator size by changing its structure, such as by using an open-loop folded half-wavelength resonator,21,22 modified shapes,19,23 and defected ground structures (DGSs).24-28 However, employing DGS requires double ground processing, which further complicates the filter design.
Artificial dielectric metamaterial (composite) structures have been shown to exhibit novel electromagnetic (EM) properties. Studies revealed that the same EM properties at microwave frequency bands cannot be obtained with conventional materials. Metamaterials are single-negative (SNG) material (in terms of permittivity or permeability) or double-negative (DNG) media.29-31
Metamaterials have been realized employing either composite-right-left-handed transmission lines (CRLH) or split-ring resonators (SRRs) or as complementary split ring resonators (CSRRs).29-31 CRLH transmission lines (TLs) which are realized by periodically loading a conventional TL with series capacitors and shunt inductors, are nonresonant structures. They have been suggested for use in to many filters.32-35
SRRs were originally proposed by Pendry et al.36 Depending on the employment configuration of SRRs, they have been used to represent SNG metamaterial. SRRs have been applied for microstrip BPFs to achieve the filter compactness because these resonators can be designed with dimensions smaller than the signal wavelength at their resonant frequency.37-39 Also, the compactness of an SRR-based filter is achieved due to the capacitive coupling introduced between the inner and outer rings.40-42 On top of that, coupled metamaterial SRRs have been used to introduce high-selectivity BPFs.43-46
To better understand the design of SRR-based BPFs, the designs of SRR BPFs of two different orders will be presented, with objectives of achieving compact sizes with high out-of-band rejection (high selectivity). Commercial computer-aided-engineering (CAE) software was used for the full-wave performance simulations of the filters, CST Microwave Studio software from CST (www.cst.com), with simultations validated by measurements of fabricated prototype filters.
Synthesizing a Filter
It’s possible to synthesize coupled filters using an optimization technique. Although other coupling techniques are known, the optimization method is also effective. Filter synthesis is based on extracting the desired coupling coefficient between resonators and the external quality factor at the input and the output resonator. The transmission function S21 (ω´) is given by refs. 8 and 9 and the following equations:
ε = [10R/10 – 1]-1/2 (2)
xn = (ω´ − 1/ωn´)/(1 − ω´/ωn´) (4)
where ω´ is the variable angular frequency, R is return loss, and ωn´ is the location of the nth transmission zero.
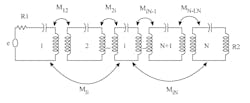
1. This simple schematic diagram shows a BPF with a number of coupled resonators.
Figure 1 illustrates a network of multiple coupled-loss resonators. The coupling coefficient between resonators i and j is denoted by Mij = Mji. The scattering parameters of the filter are calculated by eqs. 5 through 87,8:
S21 = −2j/(R1R2)0.5[A-1]N1 (5)
S11 = 1 + 2jR1[A-1]11 (6)
[A] = [ω´U – jR + M] (7)
ω´ = (ω0/Δω)[(ω/ω0) – (ω0/ω)] (8)
where R1 is the internal resistance exiting from resonator 1 and R2 is considered the load at the output that’s connected with resonator N. Parameter [U] is the identity matrix; R is a matrix with only nonzero elements of R11 = R1 and RNN = R2; and M is a symmetric square coupling matrix. Also, ω´ is the normalized angular frequency and ω0 is the center angular frequency of the filter. The sequence of filter analysis, comparison with the desired performance, and modification of the design parameters is performed iteratively until the optimum filter performance is achieved. The objective function is based on the optimization technique8 illustrated by Eq. 9:
K = ΣNi=1ǀS11(ω´zi )ǀ2
+ ΣPi=1ǀS21(ω´pi )ǀ2
+[ǀS11(ω´ = 1)ǀ - ε/(1 + ε2)0.5]2 (9)
where ω´zi and ω´pi are the zeros and poles, respectively, of the filtering function FN, which is assumed to have P poles and N zeros.
Second-Order BPF
To put Eqs. 5 to 9 to work, a second-order coupled SRR BPF was designed and fabricated according to a target set of specifications. These include a center frequency of 2.4 GHz, a passband 150 MHz, resulting in a fractional bandwidth (FBW) of BW/f0 = 0.058. The SRR BPF will be designed for a minimum return loss of 20 dB. The proposed filter synthesis for the fundamental mode is based on the coupling matrix and external quality factor extraction using Eqs. 5 to 9. A coupling matrix (M) to realize the chosen topology was optimized and extracted as:
The external quality factors are q1 = q2 = 1.5 and, hence, the actual external quality factors at input and output, Qei = Qeo, can be established by Eq. 11:
Q = q/FBW (11)
The actual (denormalized) coupling matrix becomes:
Qei = Qeo – 12.51 (12b)
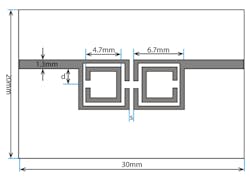
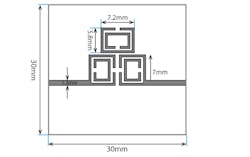
According to the coupling matrix and external quality-factor extraction, the physical structure of the coupled resonator filter is realized as a second-order filter using full-wave EM simulation. A prototype filter was fabricated in a microstrip configuration with RO6010 circuit material from Rogers Corp. The circuit material has a dielectric constant (Dk) of 10.2 in the z-axis (thickness) at 10 GHz, dielectric loss tangent of 0.0027, and thickness (h) of 1.27 mm. Two 50-Ω microstrip transmission lines are added at the filter ends. Fig. 2 shows the 2D layout of the second-order coupled SRR resonator filter.
2. This two-dimensional (2D) layout represents a second-order coupled SRR filter.
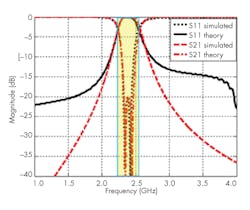
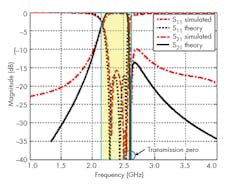
The simulated (full wave) and theoretical (circuit implementation) transmission and reflection coefficients of the coupled SRR filter are plotted in Fig. 3. It’s obvious that the center frequency of the filter equals 2.4 GHz with bandwidth of 150 MHz. Within the passband, the filter has transmission coefficient (S21) close to −0.5 dB and reflection coefficient of −20 dB.
3. By applying theory and computer simulations, the insertion and return losses can be found for the second-order coupled SRR filter.
As Fig. 3 shows, there’s good agreement between the theoretical optimized performance (employing Eqs. 5 and 6) and the full-wave simulation. The results are well-matched within the BPF passbands (2.1 to 2.7 GHz). However, above 3 GHz, a deviation exists between the prototype and simulation results. This can be claimed as a limitation of the lumped-element components used in the circuit calculations compared to the precision of the full-wave simulation. The deviation does not impact the results, however, and does not predict the presence of transmission zeros in the BPF design.
4. The second-order coupled SRR filter was fabricated on commercial circuit laminate material, with coaxial connectors attached for testing.
5. The simulated and measured losses of the second-order coupled SRR filter can be compared here.
Figure 4 shows a prototype of the BPF, while Fig. 5 shows measured S-parameters for the BPF. The center frequency is at 2.3 GHz, with bandwidth from 2.1 to 2.6 GHz. The filter achieves return loss of about −10 dB within the passband. Insertion loss of less than 0.8 dB is one deviation in the measured results that does not exist in the simulated performance. The observed frequency shift of about 100 MHz between measured and simulated results may be a result of the imperfect full-wave simulation and variations in fabrication accuracy, which cannot be totally avoided.
For the third-order BPF, the specifications include a center frequency (f0) of 2.4 GHz, bandwidth (BW) of 300 MHz (the FBW is BW/f0 = 0.125), return loss of better than 15 dB, and one single transmission zero at only 50 MHz after the upper cutoff frequency (2.6 GHz). This transmission zero increases the filter selectivity compared to the previous design.
As explained in ref. 8, this optimization technique can produce equal transmission zeros according to (N − 2), where N is the number of resonators used. Therefore, to have one transmission zero, the proposed filter in this stage is designed as a third-order coupled resonator. It’s worth noting that the position of the transmission zero is explained by the type of cross-coupling between the third resonator and the two original ones. Also, the specific value of the transmission zero was specified in the optimization equation ended by the coupling matrix. This approach is explained in detail in ref. 4, with the optimization technique described in ref. 8.
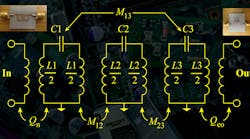
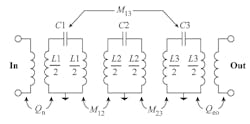
Figure 6 shows the equivalent circuit of the trisection cross-coupled filter. The resonator circuit is a LC resonant tank. Coupling coefficients M12 and M23 are considered as the coupling between adjacent resonators. Also, the cross-coupling is given by M13. Parameters Qei and Qeo are the input and output external quality factors, respectively.
6. This is an equivalent circuit of the trisection, cross-coupled third-order SRR filter.
The filter design procedures can be summarized in two steps:
1. By controlling the coupling between resonators and the external quality factor, a bandwidth of 300 MHz is achieved.
2. The location of the transmission zero is specified at 2.61 GHz
Based on the previous optimization technique of extracting the coupling matrix and the external quality factor, coupling matrix (M), which is validated for the chosen topology, is optimized and extracted using the matrix of Eq. 13:
The external quality factors are q1 = q2 = 1.009. The actual (denormalized) coupling matrix becomes:
The actual external quality factors at input and output are Qei = Qeo = 8.072.
The third-order coupled resonator filter performance is confirmed by using a full-wave EM simulation. Fig. 7 shows the 2D layout of the third-order coupled SRR BPF. The filter consists of three SRR resonators; two are direct-coupled to each other and the third cross-coupled with them.
7. The 2D layout represents the circuit pattern for the trisection, cross-coupled third-order SRR filter.
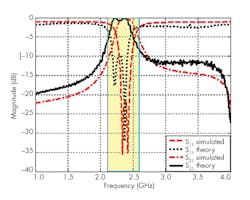
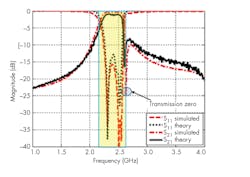
Figure 8 presents a comparison between the full-wave simulated scattering parameter magnitudes of the filter and theory, which depends on filter syntheses using the optimization technique. It’s clear that the filter center frequency is 2.4 GHz and the filter bandwidth equals 300 MHz. There’s a single transmission zero at 2.61 GHz, with this transmission zero due to cross-coupling between the resonators. Within its passband, the filter has insertion loss (S21) close to 0.3 dB and return loss of 15 dB. As Fig. 8 shows, good agreement was achieved between simulation and theory.
8. Theory and computer simulations for the third-order coupled-resonator SRR filter can be compared here.
Figure 9 shows a photograph of the fabricated third-order BPF, while Fig. 10 provides simulated and measured scattering parameter magnitudes for the filter. The measured results illustrate that the center frequency is about 2.4 GHz, with almost 15-dB return loss, close to 0.7-dB insertion loss, and with transmission zero at 2.61 GHz. This is about 0.3-dB greater measured insertion loss than the simulated value. The table below compares results for some recently published filter designs.
9. The photograph shows the third-order SRR filter, fabricated on commercial circuit material.
10. Compared are measured and simulated S-parameters for the third-order BPF.
These second- and third-order BPFs both have passbands around a center frequency of 2.4 GHz. Both are based on SRR resonators to achieve compact size (only 3 × 2 cm), and the third-order filter provides the added bonus of high out-of-band rejection for suppression of signals outside of the channel of interest. Whether simulated or measured, the filters provide performance levels in close agreement.
References
1. David M. Pozar, Microwave Engineering, Wiley, New York, 2011.
2. G. L. Jones, G. Matthaei, and Leo Young, Microwave Filters Impedance-Matching Networks and Coupling Structures, Artech House, Norwood, MA, 1985.
3. R. J. Cameron, C. M. Kudsia, and R. R. Mansour, Microwave Filters for Communication Systems: Fundamentals, Design, and Applications, Wiley, New York, 2007.
4. J. S. Hong, Microstrip Filters for RF/Microwave Applications, 2nd ed., Wiley, New York, 2011.
5. Ralph Levy, Richard V. Snyder, and George Matthaei, “Design of Microwave Filters,” IEEE Transactions on Microwave Theory and Techniques, Vol. 50, No. 3, 2002, pp. 783-793.
6. J. A. Ruiz-Cruz, C. Wang, and K. A. Zaki, “Advances in microwave filter design techniques,” Microwave Journal, Vol. 51, No. 11, November 2008, pp. 26–44.
7. J. Lee and K. Sarabandi, “Synthesizing Microwave Resonator Filters,” IEEE Microwave Magazine, Vol. 10, No. 1, 2009, pp. 57 - 65.
8. S. Amari, “Synthesis of Cross-Coupled Resonator Filters Using an Analytical Gradient-Based Optimization Technique,” IEEE Transactions on Microwave Theory & Techniques, Vol. 48, No. 9, September 2000, pp. 1559-1564.
9. F. Seyfert and S. Billa, “General synthesis techniques for coupled resonator networks,” IEEE Microwave Magazine, Vol. 8, No. 5, October 2007, pp. 98–104.
10. J. Uhm, J. Lee, I. Yom, and J. Kim, “General coupling matrix synthesis method for microwave resonator filters of arbitrary topology,” ETRI Journal, Vol. 28, No. 2, 2006, pp. 223–226.
11. C.-M. Tsai, S.-Y. Lee, and C.-C. Tsai, “Performance of a planar filter using a zero-degree feed structure,” IEEE Transactions on Microwave Theory & Techniques, Vol. 50, No. 10, October 2002, pp. 2362–2367.
12. W. Xue, C.-H. Liang, X.-W. Dai, and J.-W. Fan, “Design of Miniature Planar Dual-Band Filter With 0º Feed Structures,” Progress in Electromagnetics Research, Vol. PIER 77, 2007, pp. 493–499.
13. Pu-Hua Deng and Jen-Tse Tsai, “Design of Microstrip Cross-Coupled Bandpass Filter With Multiple Independent Designable Transmission Zeros Using Branch-Line Resonators,” IEEE Microwave and Wireless Components Letters, Vol. 23, No. 5, 2013, pp. 249 -251.
14. Jia-Sheng Hong, H. Shaman, and Young-Hoon Chun, “Dual-Mode Microstrip Open-Loop Resonators and Filters,” IEEE Transactions on Microwave Theory & Techniques, Vol. 55, No. 8, 2007, pp. 1764-1770.
15. Mahmoud A. Abdalla, Aser M. Ahmed, and A.M.M.Allam, “A Multiband Filter for Wireless and RFID Applications,” ICET 2014, Cairo, Egypt, pp. 1-4.
16. P. Mondal and M. K. Mandal, “Design of Dual-Band Bandpass Filters Using Stub-Loaded Open-Loop Resonators,” IEEE Transactions on Microwave Theory & Techniques, Vol. 56, No. 1, 2008, pp. 150-155.
17. M. Hayati, L. Noori, and A. Adinehvand, “Compact dual-band bandpass filter using open loop resonator for multimode WLANs,” Electronics Letters, Vol. 48, No. 10, 2012, pp. 573-574.
18. Chang-Soo Ahn, Juseop Lee, and Young-Sik Kim, “Design flexibility of an open-loop resonator filter using similarity transformation of coupling matrix,” IEEE Microwave and Wireless Components Letters, Vol. 15, No. 4, 2005, pp. 262-264.
19. Qing-Xin Chu and Huan Wang, “A Compact Open-Loop Filter With Mixed Electric and Magnetic Coupling,” IEEE Transactions on Microwave Theory & Techniques, Vol. 56, No. 2, 2008, pp. 431-439.
20. Huan Wang and Qing-Xin Chu, “An EM-Coupled Triangular Open-Loop Filter With Transmission Zeros Very Close to Passband,” IEEE Microwave and Wireless Components Letters, Vol. 19, No. 2, 2009, pp. 71-73.
21. Jayatilaka, C. Himal, and David M. Klymyshyn, “Half wavelength open loop bandpass filters with transmission zeros,” 2007 IEEE Asia-Pacific Microwave Conference, (APMC 2007).
22. T. Lim, B.-W. Min, and Y. Lee, “Miniaturisation method for coupledline
bandpass filters with identical and minimal number of reactive elements,”
IET Microwave Antennas & Propagation, Vol. 8, 2014, pp. 1192–1197.
23. L. Athukorala and D. Budimir, “Compact Filter Configurations Using Concentric Microstrip Open-Loop Resonators,” IEEE Microwave and Wireless Components Letters, Vol. 22, No. 5, 2012, pp. 245-247.
24. A. Boutejdar, A. Elsherbini, S. Amari, and A. S. Omar, “A New Technique to Double the Rejectband of a Low-pass Filter by Employing Coupled C-Open-Loop Resonators as Defected Ground Structure (DGS),” 2007 IEEE Asia-Pacific Microwave Conference, pp. 1-4.
25. A. Abdel-Rahman, A. K. Verma, A. Boutejdar, and A. S. Omar, “Compact stub type microstrip bandpass filter using defected ground plane,” IEEE Microwave and Wireless Components Letters, Vol. 14, No. 4, 2004, pp. 136-138.
26. P. Vagner and M. Kasal, “Bandpass filter design using an open-loop defected ground structure resonator,” 2010 15th International Conference on Microwave Techniques (COMITE), pp. 77-80.
27. Bian Wu, Xin Lai, Jia Chen, Xue-Feng Li, and Chang-Hong Liang, “Dual-mode filter with asymmetric response using square loop resonator DGS,” 2010 International Conference on Microwave and Millimeter Wave Technology (ICMMT), pp. 1298-1300.
28. Ahmed Boutejdar, Adel Elsherbini, and A. S. Omar, “Method for widening the reject-band in low-pass/band-pass filters by employing coupled C-shaped defected ground structure,” IET Microwaves, Antennas & Propagation, Vol. 2, No. 8, 2008, pp. 759-765.
29. N. Engheta and R. W. Ziolkowski, Electromagnetic Metamaterials: Physics and Engineering Explorations, Wiley, Hoboken, NJ, 2006
30. C. Caloz and T. Itoh, Electromagnetic Metamaterials Transmission Line Theory and Microwave Applications, Wiley, Hoboken, NJ, 2006.
31. G. V. Eleftheriades and K. G. Balmain, Negative Refractive Metamaterials, Wiley, Hoboken, NJ 2005.
32. Mohammed A. Fouad and Mahmoud A. Abdalla, “Ultra Compact CPW Dual Band Filter Based on Π-Generalized Metamaterial NRI Transmission Line,” Journal of Electromagnetic Waves and Applications, Vol. 29, No. 8, 2015, pp. 1093-1103.
33. Mohammed. A. Fouad, and Mahmoud A Abdalla, “A New π-T Generalized Metamaterial NRI Transmission Line for a Compact CPW Triple BPF Applications,” IET Microwave, Antennas & Propagation, Vol. 8, No. 13, 2014, pp. 1097-1104.
34. Ki-Cheol Yoon, Hyun-Wook Lee, Jong-Chul Lee, and Seong-Cheol Kim, “A Dual-Band Narrow Band-Pass Filter With Half-Wavelength Open Stubs Using The CRLH Metamaterial,” Microwave and Optical Technology Letters, Vol. 55, No. 8, 2013, pp. 1887-1890.
35. Mahmoud Abdalla, A. Y. Hassan, and A. M. Galal Eldin, “A Compact High Selective Coupled Gap CRLH TL Based Bandpass Filter”, 2015 9th International Congress on Advanced Electromagnetic Material in Microwave and Optics, September 7-12, 2015, United Kingdom.
36. J. B. Pendry, A. J. Holden, D. J. Robbins, and W. J. Stewart, “Magnetism from conductors and enhanced nonlinear phenomena,” IEEE Transactions on Microwave Theory & Techniques, Vol. 47, 1999, pp. 2075-2084.
37. Q. Xiang, Q. Feng, and X. Huang, “Tunable Bandstop Filter Based on Split Ring Resonators Loaded Coplanar Waveguide,” ACES Journal, Vol. 28, No. 7, 2013.
38. A. K. Horestani, M. Duran-Sindreu, J. Naqui, C. Fumeaux, and F. Martin, “Coplanar Waveguides Loaded with S-Shaped Split-Ring Resonators: Modeling and Application to Compact Microwave Filters,” IEEE Antennas and Wireless Propagation Letters, Vol. 13, 2014, pp. 1349-1352.
39. Jian Li, Yongjun Huang, Guangjun Wen, Xiaolin Xue, and Jiaming Song, “Compact and high-selectivity microstrip bandpass filter using two-stage twist-modified asymmetric split-ring resonators,” Electronics Letters, Vol. 51, No. 8, 2015, pp. 635-637.
40. A. Velez, F. Aznar, J. Bonache, M. C. Velazquez-Ahumada, J. Martel, and F. Martin, “Open complementary split ring resonators (OCSRRs) and their application to wideband CPW band pass filters,” IEEE Microwave and Wireless Components Letters, 2009, pp. 197-199.
41. M. A. Abdalla, M. A. Fouad, H. A. Elregeily, and A. A. Mitkees, “Wideband negative permittivity metamaterial for size reduction of stopband filter in antenna applications,” Progress in Electromagnetics Research C, Vol. 25, 2012, pp. 55-66.
42. Q.-L. Zhang, W.-Y. Yin, S. He, and L.-S. Wu, “Evanescent-mode substrate integrated waveguide (SIW) filters implemented with complementary split ring resonators,” Progress in Electromagnetics Research, Vol. 111, 2011, pp. 419-432.
43. J. Garcia-Garcia et al., “Miniaturized Microstrip and CPW Filters Using Coupled Metamaterial Resonators,” IEEE Transactions on Microwave Theory and Techniques, Vol. 54, No. 6, 2006, pp 2628-2635.
44. H. Nornikman, B. H. Ahmad, M. Z. A. Abdul Aziz, M. F. B. A. Malek, H. Imran, and A. R. Othman, “Study and simulation of an edge coupled split ring resonator (Ec-Srr) on truncated pyramidal microwave absorber,” Progress in Electromagnetics Research, Vol. 127, 2012, pp. 319-334.
45. L. Zhou, S. B. Liu, X. K. Kong, and Y. N. Guo, “Novel cross-coupled filter design using improved split-ring resonators based on stepped impedance resonator,” Microwave and Optical Technology Letters, Vol. 53, No. 9, 2011, pp. 1976-1980.
46. S.-H. Jang, and J.-C. Lee, “Design of novel cross-coupling elliptic function filters with the miniaturized edge-coupled split ring resonators,” Microwave and Optical Technology Letters, Vol. 45, June 2005, pp. 495-499.