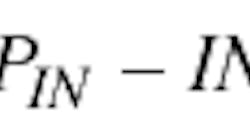Transmitters require circuitry to measure and control RF power for proper operation. Since system requirements vary widely, a power-control circuit may be as simple as a low-dynamic-range diode detector. The whole purpose for this device is to detect catastrophic events such as the sudden increase in VSWR that might occur when an antenna breaks. But for more complex power detection control, as in a GSM base-station transmitter, an RF power detector may need measurement uncertainty of less than ±1 dB over an input power range of 60 dB or more. There are many ways to control RF power, but ever-improving logarithmic-amplifier (logamp) technology offers many solutions.
The GSM transmitter is an example of a demanding application. A +47-dBm (50-W) transmitter operating at full power must transmit a power level between +45 and +49 dBm1 (+44.5 to +49.5 dBm under extreme conditions). To stabilize the output level, the amplitude of the transmitter's input signals must be precisely known, often within ±1 dB over a wide dynamic range.
There are a number of ways to measure this power, including the use of a closed-loop architecture (Fig. 1a). In this approach, a directional coupler (with typically 10 to 30 dB coupling) is used to sample power from the power amplifier (PA) to the antenna. Some additional attenuation is generally necessary to reduce the power within the safe measurement range of the detector. This measured result is compared to a set-point voltage; the difference drives an integrator (also commonly referred to as an error amplifier).
The error amplifier's output will rise or fall until the output power of the PA corresponds to the set-point voltage. The error amplifier will not necessarily drive the bias control of the PA; the system will be just as effective if the PA has fixed gain and the error amplifier is used to control the gain of an intermediate-frequency (IF) variable-gain amplifier (VGA).
This type of power control (known as controller mode from the perspective of the detector) is useful in systems requiring fast control of power, such as time-division-multiple-access (TDMA) systems where power is transmitted in precisely timed bursts. The fast "local" control allows the power to be ramped up and down in a controlled fashion. If a logarithmic detector is used, the power can be controlled over a large dynamic range (typically 40 to 60 dB).
Figure 1b shows a power control loop where the detector output is digitized. Software in the digital signal processor (DSP) or microcontroller makes a decision based on the measured result and then adjusts output power using a digital-to-analog converter (DAC). Since this arrangement does not allow for fast control, it is more useful in systems where power is transmitted continuously, such as CDMA, WCDMA, and TD-SCDMA systems. With digital control, extra calibration can be added to the measurement loop. For example, if the power detector drifts (but with good repeatability) with temperature, a compensation algorithm can be implemented if the system contains a temperature sensor.
Figure 1c shows a wireless transmitter with an auxiliary receiver in which the signal being transmitted is sampled and mixed back down to baseband. The use of an auxiliary receiver is common in HPA linearization schemes such as feedforward and digital pre-distortion, where it provides feedback to the algorithm about the quality of the transmitted spectrum. In this implementation, measurement of transmitted power comes for free. The measurement will be accurate as long as the gain of the receiver does not vary significantly with temperature or frequency.
Figure 1d shows alternative power control architecture used in some handsets. The architecture assumes that the transmitted power should be determined based on the received power. For example, if the received power is decreasing, the transmitted power should be increased. This is a slow and somewhat imprecise system. However, it is a useful way to set power during the initiation of a link.
In general, power-measurement accuracy is most critical when the PA is at, or close to, full power. For example, in a +50-dBm (100-W) transmitter, a 1-dB error in the voltage from the power measurement circuit will result in a transmitted power of +51 dBm (126 W). This forces the PA to be over-dimensioned by 25 percent (making it physically larger and more expensive) to guarantee safe operation. However, at low power levels, the tolerance of the output power is only required to be within the limits of the wireless standard.
The temperature stability of the detector in these applications is critical. Traditionally, diodes have been used to perform this function. While diode detectors have good temperature stability when driven hard (good performance is generally achieved at input powers in the +15 dBm range), they have limited dynamic range (20 to 30 dB) and drift severely at low input power levels.
Demodulating logamps are becoming an increasingly popular choice when systems call for measurement and control of RF power. Figure 2 shows the transfer function of a logamp at 2.2 GHz. The AD8318, specified from 0.001 to 8 GHz, was used to generate this plot. The figure shows output voltage and calculated error, both versus input power.
As the input power varies from 65 to 0 dBm, the output voltage varies from 2 V to about 0.5 V.
Calibration is required to achieve the rated accuracy of a log detector. This is true even if the detector is factory trimmed. Looking again at Fig. 1, we can see that there can be uncertainty about the signal level reaching the logamp. Signal trace losses, and part-to-part variability in the coupling factor of the directional coupler and attenuator can easily produce 1 dB or more of uncertainty.
The recommended method of calibration is to set the PA output to two or more approximate levels and measure the detector's output voltage.
Within its linear operating range, a logamp with approximately follow the equation:
Slope is the incremental change in output voltage for a corresponding change in input power (unit is mV/dB). The intercept is the point (in dBm or dBV) at which the extrapolated linear transfer function touches the x-axis.
Page Title
In general, the calibration is performed by applying two power levels (one at the top end of the input range and one at the bottom end) and measuring the corresponding output voltages from the detector. Calculation of slope and intercept is done using the Eqs. 2 and 3.
Once SLOPE and INTERCEPT have been calculated, Eq. 4 can be written which will allow calculation of an (unknown) input power based on the output voltage of the detector.
Using the ideal equation for output voltage (Eq. 1) as a reference, the log conformance error of the measured data can be calculated with Eq. 5.
Figure 2 includes a plot of the error at +25C, the temperature at which the logamp is calibrated. Note that the error is not zero. This is because the logamp does not perfectly follow the ideal Vout versus Pin equation, even within its operating region. The error at the calibration points (12 and 52 dBm in this case), however, will be equal to zero by definition.
Figure 2 also includes error plots for the output voltage at 40 and +85C. These error plots are calculated using the SLOPE and INTERCEPT at +25C. This is consistent with calibration in a mass-production environment where calibration over temperature is not practical.
It is possible to improve narrowband performance at higher power levels by changing the calibration points (data not shown), although the error functions will change. The shape of these error functions will vary as the calibration points are changed. Using calibration points of 10 and 30 dBm, for example, results in an error of 0 dB at +25C at these calibration points. In the range between the calibration points, the errors at ambient temperature and over all operating temperatures are very small. At lower power levels from 30 to 60 dBm, however, the error degrades. This calibration scenario might be used in a transmitter where precision is most critical near full power. In general, the calibration points should be selected at the boundaries of the range over which the highest precision is desired.
Calibration points should therefore be chosen to suit the application at hand. In general, though, the calibration points should never be chosen in the nonlinear portion of the logamp's transfer function (above 5 dBm or below 55 dBm in this case).
The error function of a logamp detector can also be analyzed in terms of the dB error values at various temperatures with respect to the output voltage at ambient temperature. Until now, errors have been plotted with respect to the ideal transfer function at ambient temperature. Using this alternative technique, the error at ambient becomes equal to 0 by definition. This would be valid if the device transfer function perfectly followed the ideal Vout = Slope(Pin Intercept) equation. However, since a logamp in practice will never perfectly follow this equation, especially outside of its linear operating range, this plot tends to artificially improve linearity and extend the dynamic range. This plot is a useful tool to estimate the temperature drift at a particular power level with respect to the (nonideal) output voltage at ambient.
Until now, performance plots have focused on individual devices. However, in a mass-production environment, the worst-case performance must be considered. To do this, it is necessary to look at the transfer functions and error plots of a population of devices. Figure 3 shows the output voltages and errors of multiple AD8318 logamps measured at 5.8 GHz. The concentration of black plots represent the performance of the population at +25C (the slope and intercept has been calculated for each device). The red and blue plots of error indicate the measured behavior of a large population of devices over temperature. This suggests a range on the drift (from device-to-device) of 1.2 dB with worst-case drift at 40C. If operation to 10C or even 20C is desired, the temperature drift will be much smaller.
The AD8318 functionality includes the capability to externally trim the temperature drift. Attaching a ground-referenced resistor to the TADJ pin alters an internal current that works to stabilize intercept drift versus temperature. As a result, the TADJ resistor can be optimized for operation at different frequencies. While the TADJ resistor could be chosen on a device-by-device basis, this is not practical since each logamp would have to be characterized for temperature drift. In practice, the population information supplied in Fig. 3 can be used to choose the value of TADJ resistor that will yield the best overall drift.
In time-division multiplexed applications, the RF detector must be able to quickly respond to large-signal changes at the input. In a controller mode application (Fig. 1a), the detector must have a response time (the term video bandwidth is commonly used) that is fast enough so that the dominant pole of the control loop is set by the capacitor of the integrator.
Figure 4 shows the output of the AD8318 in response to a short RF burst. Because the slope of the logamp is negative, the output falls after the onset of the burst with a 90-to-10-percent fall time of 11.4 ns. This response time is more than adequate for almost all power measurement applications. This extremely fast response time also opens up more application possibilities such as radar receivers or amplitude-shift-keying (ASK) detection.
The ripple in the response of the detector, at twice the input frequency, is a by-product of the logarithmic transformation. Because of the high video bandwidth of the logamp, these artifacts will be present when the input signal is at a relatively low frequency. A lowpass filter can easily eliminate this ripple, but this will come at the expense of some response time. At high input frequencies (greater than 100 MHz), the internal video bandwidth will remove all ripple.
Logamp detectors that can accept input frequencies up to 8 GHz are beginning to replace the more traditional diode detectors. Out-of-the-box temperature stability is much better than 1 dB and holds up over a large dynamic range. Response time is fast enough for use in radar and ASK-detection applications. For more information on the AD8318, visit the Analog Devices website at www.analog.com/AD8318.
REFERENCE
1. GSM Standard for Radio Transmission and Reception ETSI TS 100 910 V8.9.0 (2001-04), page 14.