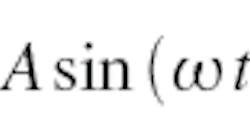Coaxial cables had once been thought to support only a single transverse-electromagnetic (TEM) propagation mode. But a solution to the Maxwell-Heaviside equations supports the existence of a propagating transverse-magnetic (TM) surface-wave mode as well. This mode is suppressed by the outer conductor in coaxial cables of conventional impedance, but is dominant in higher-impedance coaxial cables and also on a single uninsulated and unconditioned conductor having no outer shield. This non-radiating surface-wave mode, which has practical uses at RF through microwave frequencies, can exhibit very low attenuation and a relative propagation velocity of unity. This first installment of a three-part article will introduce this surface-wave mode and propose some applications using overhead power distribution lines for last-mile communications applications.
Coaxial cable is perhaps the most commonly used transmission line type for RF and microwave measurements and applications. In 1894, Heaviside, Tesla, and others received patents for coaxial line and related structures. A development of coaxial-line theory is often provided as part of basic physics and engineering education,1 even prior to full development and use of the Maxwell-Heaviside equations, which are generally used for transmission line and macroscopic electromagnetic (EM) analysis. Accordingly, the analysis, measurement and application of coaxial lines are usually considered to be quite mature and complete.
Figure 1 shows the basic concept of a coaxial line. Lossless cylindrical central and outer shielding conductors are separated by a volume of empty space. This structure conveys power between two points. One end is considered an input port and driven with a sinusoidal voltage source of magnitude A at frequency Ω :
This source is applied to the line through a known impedance, ZS. The other end of the line is terminated by a load of impedance ZL.
Heaviside's telegrapher's equation provides a lumped-circuit equivalent of an infinitesimal length of transmission line. For the lossless case where R = G = 0, Ampere's Law can be used to find the inductance per unit length:
Gauss's Law can be used to find the capacitance per unit length:
This line exhibits an entirely real characteristic impedance of
which is dependent only on the geometry of the conductors (b/a). The maximum transfer of power between
the source and the load occurs when all of these impedances are equal and
Current entering the line central conductor produces a real current density, J. By Ampere's circuit law, this produces an orthogonal magnetic field B which, in vector form, is:
in the region of empty space inside the outer conductor. An equal magnitude by opposite sense current density, -J, returning from the outer shield also contributes to magnetic flux within this region. Beyond this region, the magnetic effects exactly cancel and no fields due to currents are present (the shielding nature of coaxial cable).
Between the conductors, the varying magnetic (B) field produces an electric field according to Eq. 7:
The electric field lines extend between the conductors and are normal to their surfaces. These electric and magnetic fields produce a TEM wave that travels along the line in the space between the two conductors. In the example coaxial line, this wave travels in a vacuum without attenuation and with velocity of light in a vacuum.
Waves propagating on transmission lines can be described in terms of the axes of the electric or magnetic fields and a mode number. One or both of the electric and magnetic fields must be transverse to the direction of propagation. The corresponding modes are transverse electric (TE), transverse magnetic (TM), and TEM in nature. A pair of mode numbers, n and m, represent the order of the mode in the transverse and longitudinal directions, respectively. Values of zero for each describe a principal mode in the corresponding direction.
For a coaxial line of infinite length and for wavelengths that are large compared to the inner circumference of the outer conductor,
there is radial symmetry and the coaxial line exhibits a principle TEM00 propagation mode. The impedance presented to the source by the line can be written as
where
= 4 10-7 H/m ≈ 1.2566 H/m (the permeability of a vacuum) and
e = 1/(c2) F/m ≈ 8.8542 pF/m (the permeability of a vacuum)
For the matched condition described here, the voltage produced by the wave at a position separated from the source by a distance l along the line can be described as:
where y = α + jβ is the proportionality constant. Parameter describes the attenuation while parameter describes the phase per unit length of line. The propagation constant for the principle mode can be shown to relate to the components in Fig. 1 by
which for the lossless case is purely imaginary and the same as that of the enclosed medium.3
Continue to page 2
Page Title
Practical cables require dielectric supports and use imperfect conductors. This complicates modeling efforts, but more than a century of use has validated this basic understanding of coaxial line and its application to the solution of real-world problems. For most applications from RF through upper microwaves, conveniently dimensioned coaxial cable has proven to be an excellent component for transferring electromagnetic energy between different locations without significant radiation; it also effectively shields the internal wave from external components and circuitry.
A homogeneous plane wave in an isotropic medium has the intrinsic impedance in free space of Eq. 12.4
where σ = 0. This reduces to Eq. 13:
In a coaxial line, as the geometry b/a increases, the impedance of the TEM00 mode increases logarithmically and the real current density, J, tends towards zero. Equating Eqs. 2 and 3 shows that the impedance of the TEM00 mode in coax equals that of free space when the conditions of Eq. 14 are satisfied.
But the propagation speed of energy in a vacuum cannot exceed the speed of light in a vacuum per Eq. 15:
Just as for a planar wave in free space, energy propagating through a lossless coaxial transmission line having vacuum dielectric and no magnetic materials is subject to this constraint. The impedance associated with the propagating energy in a transmission line is bounded by the permeability and permittivity of space. Energy may propagate simultaneously by way of a hybrid of multiple modes but the combined impedances or admittances of the propagating modes are bounded such that for the total propagating wave as per Eq. 16:
For a line with dimension meeting Eq. 8, due to symmetry, only modes with a TM component, either TEM or TM, are possible since any asymmetric modes that would produce a longitudinal magnetic component will be immediately damped out.2 Only TEM0m or TM0m modes can propagate. For perfect conductors, only principal modes are supported.3 So, only TEM00 or TM00 modes are possible.
In coaxial lines of this type, the combined admittances of these conductors must be bounded according to Eq. 17
The admittance due to the TEM00 mode can be found from Eq. 18:
It is positive, finite, and continuous over the range described in Eq. 19:
So, at least for the case where ln(a/b) > 2Π, a propagating TM00 mode must also exist and provide a finite admittance (Eq. 20):
All propagating modes are solutions to the wave equation, which results from Maxwell's equations and satisfy the requirements for continuity of fields at the conductor-vacuum boundary. Combinations of Bessel functions are used to describe the fields and impedances associated with these solutions. These functions and their first derivatives have singularities only at zero and infinity and are continuous in between. Therefore, the fields and waves they describe also are without discontinuities over the intermediate region.
As a result, it is possible to extend the above observation regarding the existence of simultaneous propagating TEM00 and TM00 modes in coaxial lines to include the range for all geometries according to Eq. 21:
A TM wave on a single conductor embedded in a dielectric medium can be viewed as a surface wave along the inner conductor of a coaxial line having infinite geometry. With the view in mind, for finite VS, the real current density vanishes:
As the geometry of the coaxial line increases without bound, the component of the magnetic field due to the longitudinal component of the displacement current increases at the same time that the component due to real current decreases, according to Eq. 24:
In the limit, the amount of real current terminating in the outer conductor falls to zero and the total admittance is due entirely to displacement current, which produces a single principle TM00 mode with the same impedance as a wave in free space.
For intermediate geometries, the total admittance is due to contributions from each mode. The outer conductor provides a path for real return current, which increases the total admittance. This increase in admittance reduces the potential on the line and causes an associated reduction of longitudinal displacement current and a corresponding decrease in the portion of the total power propagated via the TM mode.
Thus, conventional coaxial cable always propagates power by a hybrid of a principal TEM mode and a principal TM mode over the entire range of coax geometries. Both of these modes have the same propagation constant, which is that of the enclosed dielectric. For the case of perfect conductivity and vacuum dielectric both waves travel without attenuation at the speed of light.
Sommerfeld investigated surface waves3 as did Zenneck,4 particularly involving lossy conductors as part of achieving an understanding of beyond- the-horizon radio propagation during the early 1900s. Solutions for the wave around a perfectly conducting center cylinder embedded in a dielectric were presented by Stratton in 1941. There it was found that only a single modal low-attenuation solution describing a TM00 wave having the same propagation constant as that of the enclosing dielectric exists.5 Solutions for coaxial lines were also investigated but all except a single principle TEM00 mode were described as being inconsequential for line dimensions that are common in communications systems.6 A single principle TEM00 mode was found to dominate.
Continue to page 3
Page Title
Next month, the second part of this series will provide a description of the TM mode on an unshielded and unconditioned conductor by showing models and measurements of fields, impedance, and transmission characteristics of practical lines. This second installment will also detail the design and implementation of launchers to convert between conventional transmission lines and a line supporting this mode.
REFERENCES
1. Halliday and Resnick, Physics, Part II, Wiley, New York, 1962.
2. Julius Adams Stratton, op. cit. p. 546.
3. Julius Adams Stratton, op. cit. p. 529.
4. Zenneck, Ann. Phys. 23 (1907), 846 (referenced from ref. 13).
5. Julius Adams Stratton, op. cit. p. 527.
6. Julius Adams Stratton, op. cit. p. 549.