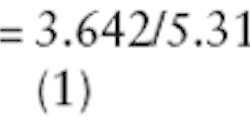Dielectric resonators (DRs) are commonly associated with high-quality-factor (high-Q) oscillators, although they can also be used to form compact antennas. To demonstrate the effectiveness of antenna design with DRs, a rectangular dielectric resonator antenna (DRA) was developed with target frequency range between 2 and 4 GHz and center resonant frequency around 3 GHz. The design goal was to achieve antenna return loss of less than 10 dB to accommodate an efficient antenna feed. As will be shown, the final design obtained an impedance bandwidth between 2.7125 and 2.7641 GHz with high gain and efficiency.
Low-loss DR materials offer a more compact alternative to the waveguide cavity resonator and also a more adaptable technology for printed circuit integration. Compact antenna size is particularly critical for portable wireless applications. In addition, DRA shapes and hybrid antennas show promise to meet the requirements for the promising broadband and ultrawideband systems.1-3
A DRA can be considered a better choice than antennas based on conventional low-gain elements such as dipoles, monopoles, and microstrip patches. A DR exhibits resonance for a narrow range of frequencies, generally in the microwave band.4 Resonators such as DRs are useful in RF communication equipment in connection with filters, low-noise oscillators, cavity resonators, and other circuits. In an antenna, a DR offers many benefits. It has no metallic loss and offers high radiation efficiency through millimeter-wave frequencies. In addition, a DRA can be made much smaller than conventional metal antennas.5 Also, a DR features mechanical simplicity and simple coupling schemes to all commonly used transmission lines. The DRA has high radiation efficiency due to the absence of con duction or surface losses and the ease of excitation. The DRA is also more resistant to proximity detuning when it is placed adjacent or close to another object.6
In this study, a DRA was designed with a rectangular cross-sectional area, and will be termed a rectangular DRA. Various other DRA shapes have been implemented in the past, but the rectangular shape was chosen since it is the easiest shape to fabricate.7-9 The rectangular shape offers a second degree of freedom, which is more than a cylindrical DRA (one degree of freedom) or a hemisphere DRA (zero degree of freedom), making it the most versatile among the basic shapes.10,11
The DRA in this study was positioned symmetrically with its Y-axis in the direction of the feedline. A vertical copper strip of height, H and width, W was attached to the DRA's flat surface. This copper strip is connected electrically to the feedline at length L1 from its open end. Among the parameters that would affect the resonant frequency are the height of the vertical copper strip (H), the length of the transmission line (L1), and the width of the transmission line (W). In addition, the DRA's dimensions will greatly affect the resonant frequency and the Q-value.
The DRA is designed using RO4003C low-dielectric-constant substrate material from Rogers Corp. with a dielectric constant of only 3.38. The choice of the dielectric material plays a significant part in the design of the DRA. Due to varied research, a ceramic dielectric was chosen to be implemented in the design of the DRA. The ceramic dielectric uses high dielectric constant bismuth titanate, Bi3Ti4O12, which has a dielectric constant of 90. After fabrication, the antenna was tested for performance, using appropriate test equipment, such as a material analyzer and a vector network analyzer (VNA). Comparisons are then conducted to observe the efficiency of the designed antenna. The transmission line uses copper, which is a conducting material, in order to function as a feeding channel. The width, W, of transmission line was calculated to be 1.9 mm. This width of the transmission line will provide an input impedance of 50 Ω .
With the objective of designing a DRA with a 3-GHz resonant frequency, the project was completed successfully with the resonant frequency around 2.7 GHz both in computer-simulated and measured results. At a resonant frequency of 2.7 GHz, the return loss differs only by 3.4 percent between simulated and measured results. Other parameters, such as gain, directivity, and efficiency, were also in close agreement between simulations and measurements.
The simulated and measured results are plotted on the same graph in Fig. 3. Figure 3 shows a graph of S11 log magnitude in dB (-20logS11). The simulation shows the resonant frequency at 2.735 GHz. It is clearly seen that the return loss is the lowest at 30.96 dB. For the measured results, the reflection coefficient is lowest between 2.67 and 2.72 GHz. At 2.69 GHz, the reflection signal of -48.1dB is lowest at the receiver. The results between the measured and simulated graph of S11 log magnitude (dB) were found to match closely. Meanwhile, the -10-dB impedance bandwidth of this rectangular DRA is 0.05 GHz. The simulated and measured results agree well over the whole operating frequency range. Thus, the bandwidth of this rectangular DRA was found to be around 50 MHz. The slight mismatches between these two results are due to variations and deviations in the fabrication process of the ceramic dielectric and the microstrip transmission line. Also, an SMA connector is attached to the microstrip by means of soldering, which may cause extra conductivity and disturb the surface current of the DRA.
The gain and the directivity of the proposed antenna were also examined. Gain is closely related to directivity, while directivity is influenced by the radiation pattern. Due to the antenna losses, such as Ohmic losses, the gain is usually less than the directivity. From Fig. 4, it can be seen that the gain of the DRA is around 3.642 dB. This means that at 2.735 GHz, the DRA's radiation has a gain of 3.642 dB, which is satisfactory for an antenna. Figure 4 also shows the directivity at 5.310 dBi, and efficiency is around 68 percent, which is considered acceptable performance to deliver 68 percent of received power to a receiver. As in Eq. 1, the efficiency, ?e, can be calculated as
This is in conformance with the simulated value of 68 percent in Fig. 4.
Figure 5 shows the simulated and measured results for the phase of the designed DRA. The simulated S11 phase differs from the measured results. The simulated result has two phase changes, unlike the measured results where there are three phase changes from 2 to 4 GHz. In the simulated graph, the phase change at 2.735 GHz is 19.09 deg. while the measured phase change at 2.735 GHz is 150.44 deg, or a difference of 131.35 deg. between the two results in Fig. 5.
Figure 6 shows a Smith Chart of the simulated and the measured impedance for the rectangular DRA. The port impedance, Zo, is 50 Ohms. The input impedance is the impedance presented by the antenna at the terminal. In Fig. 6(a), the resonant frequency of 2.735 GHz has an input impedance of (49.16-j3.556) Ohms. This means that the antenna poses an input resistance, Rin = 49.16 Ohms at its terminal. Meanwhile, the input reactance, Xin, is the power that is stored within the near field of the antenna. In this DRA design, Xin = 3.556 Ohms.
Figure 6(b) shows the measured input impedance to be (49.06+j0.58) Ohms. There is only 0.10 Ohms and 0.20 percent difference between both the simulated and measured results. The simulated and measured input resistance is almost the same, which is about 49 Ohms. Both the simulated and measured DRA is approximately equal to the characteristic impedance of 50 Ohms.
The ideal VWSR would be one where the antenna will have perfect impedance match and a maximum power transfer from the source to the load or antenna. Figure 7(a) illustrates VWSR at 2.735 GHz with its amplitude to be 1.058:1. From Fig. 6(b), with a VSWR value of 2.0:1, the obtained impedance bandwidth is 0.055222 GHz from 2.71 to 2.76 GHz. This bandwidth is in accordance with the bandwidth obtained from the S11 log magnitude graph in Fig. 6(b).
Figure 7(b) shows the VSWR measured with a network analyzer. From 2 to 4 GHz, the VSWR was found to be 1.04:1, or greater than unity. Figure 7 compares the VSWR for the simulated and measured results. As observed, the resonant frequency measured rejection was more than -30 dB at the midband frequency of the notched band and upper stopband with 15-dB attenuation to 20 GHz. A metallic enclosure used with the filter had little effect on the filter's response, with only a slight shift downward in frequency for the cutoff frequency of the upper stopband.
Continue to page 2
Page Title
In conclusion, a compact UWB bandpass filter with a highly rejected notched band and improved out-ofband performance was proposed and implemented. By tuning the parameters of these units, the proposed UWB bandpass filter can achieve a wideband passband while also offering a narrow notch within the passband. The measured results for the fabricated filter were in good agreement with simulated performance. The filter's simple planar geometry makes it compatible with existing microwave-integrated-circuit (MIC) fabrication methods.
REFERENCES
1. United States Federal Communications Commission, "Revision of Part 15 of the commission's rules regarding ultra-wideband transmission systems," Tech. Rep. ET-Docket 98153, FCC0248, Federal Communications Commission, April 2002.
2. W. Menzel, M. S. R. Tito, and L. Zhu, "Low-loss ultrawideband (UWB) filters using suspended stripline," in Proceedings of the 2005 Asia-Pacific Microwave Conference, Vol. 4, 2005, pp. 21482151.
3. K. Li, D. Kurita, and T. Matsui, "An ultra-wideband bandpass filter using broadside-coupled microstrip-coplanar waveguide structure," in IEEE MTT-S International Digest, 2005, pp. 675678.
4. N. W. Chen and K. Z. Fang, "An ultra-broadband coplanar- waveguide bandpass filter with sharp skirt selectivity," IEEE Microwave and Wireless Component Letters, Vol. 17, No. 2, February 2007, pp. 124126.
5. N. Thomson and J. S. Hong, "Compact ultra-wideband microstrip/coplanar waveguide bandpass filter," IEEE Microwave and Wireless Component Letters, Vol. 17, No. 3, March 2007, pp. 184186.
6. L. Zhu, W. Menzel, K. Wu, and F. Boegelsack, "Theoretical characterization and experimental verification of a novel compact broadband microstrip bandpass filter," in Proceedings of the Asia-Pacific Microwave Conference, 2001, pp. 625628.
7. L. Zhu, S. Sun, and W. Menzel, "Ultrawideband (UWB) bandpass filters using multiple-mode resonator," IEEE Microwave and Wireless Component Letters, Vol. 15, No. 11, 2005, pp. 796798.
8. L. Zhu and H. Wang, "Ultra-wideband bandpass filter on aperturebacked microstrip line," Electronics Letters, Vol. 41, No. 18, 2005, pp. 10151016.
9. H. Wang, L. Zhu, and W. Menzel, "Ultra-wideband (UWB) bandpass filters with hybrid microstrip/CPW structure," IEEE Microwave and Wireless Component Letters, Vol. 15, No. 12, 2005, pp. 844846.
10. H. Shaman and J. S. Hong, "Ultrawideband (UWB) bandpass filter with embedded band notch structures," IEEE Microwave and Wireless Component Letters, Vol. 17, No. 3, 2007, pp. 193195.
11. H. Shaman and J. S. Hong, "Asymmetric parallelcoupled lines for notch implementation in UWB filter," IEEE Microwave and Wireless Component Letters, Vol. 17, No. 3, 2007, pp. 516-518.
Figure 1
Figure 2