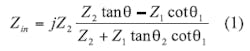Ultrawideband (UWB) communications technology provides a practical means of low-power, high-data-rate transmissions over short distances, such as in personal-area networks (PANs). The technology is also suitable for longer-range applications, such as radar systems. High-performance filters with adequate bandwidths are essential in order for UWB systems to co-exist with current wireless communications systems. The design of such filters is not trivial, although a number of approaches have been developed based on the use of stepped-impedance resonators (SIRs) capable of providing 3-dB bandwidths of greater than 100 percent of a center frequency.
UWB technology was once associated with pulsed communications, although standards bodies such as the US Federal Communications Committee (FCC) and the International Telecommunications Union's Radiocommunications Sector (ITU-R) now define UWB communications in terms of antenna transmissions with bandwidth that exceeds the lesser of 500 MHz or 20 percent of the center frequency. Under such guidelines, it is also possible to transmit signals comprised of many narrowband carriers that occupy a total bandwidth of 500 MHz or more, such as in an orthogonal-frequency-division-multiplex (OFDM) arrangement. Because carrier-based communications systems can be subject to the effects of fading and intersymbol interference (ISI), some UWB system designs opt for the use of pulsed signals at relatively high repetition rates, with the pulse energy occupying the full allotted bandwidth. In either case, filtering requirements can be challenging for UWB systems, requiring extremely wide fractional bandwidths.
The FCC has set aside the frequency band from 3.1 to 10.6 GHz for unlicensed radio use, including for UWB systems. The FCC's Part 15 power spectral density emission limit for UWB emitters in that band is -41.3 dBm/MHz, which also applies to unintentional emitters in that band. The emission limit for UWB emitters is considerably lower outside of that band, as low as -75 dBm/MHz.
The authors succeeded in designing and fabricating a filter for UWB applications using planar microstrip technology. The filter features a 3-dB fractional bandwidth of greater than 100 percent based on the use of SIRs. The design incorporates frequency-selective coupled-line sections for inducing transmission zeros, as well as tapped open-circuit stubs based on SIRs to control the transmission zeros. An additional degree of freedom was achieved in the design by using a T-shaped stub at the end of the openended stub. With measured performance that matches closely with the results from an electromagnetic (EM) software simulation tool, the simplicity of the filter topology lends itself to manufacturing processes.
Planar bandpass filters (BPF) that are small in size and deliver high selectivity, wide passbands with low insertion loss, and good stopband rejection are required for next-generation satellite and mobile communications systems. For the design of a planar filter, the electrical performance in terms of out-of-band rejection and in-band transmission losses must be weighed along with the cost, reliability, and physical size. For example, waveguide filters are commonly used in satellite-communications (satcom) applications. Although they feature extremely low passband insertion loss with high out-of-band rejection, they tend to be physically large and expensive to machine. They also typically exhibit relatively narrow passbands.
Filters designed for UWB applications over the frequency range of 3.1 to 10.6 GHz typically require a high-order configuration that results in excessive passband insertion loss and a physically large size. In addition, filters for communications applications should have flat group-delay performance in order to ensure distortion- free propagation especially with digital-modulation formats. Traditional filter design approaches fail to meet these requirements due to tight coupling and uncontrolled nonlinear frequency dispersion over the wide bandwidth of interest.
An UWB bandpass filter realized on lossy dielectric material resulted in high insertion loss of 6.7 dB.1 Filter configurations using cascaded ring resonator sections with open stubs can achieve respectable insertion-loss performance, but are limited in bandwidth compared to the requirements of UWB communications systems.2 It is possible to meet the bandwidth requirements of UWB systems by means of coupled lines using backside apertures on the ground plane for enhancing the coupling performance, and interdigital coupled lines with multimode resonators for effective coupling over a wide bandwidth.3,4 These structures require tight fabrication tolerances and are sensitive to the proximity effect of the metal enclosures and the fields generated by other components, for example, when packaged with RF integrated circuits (ICs). Electromagnetic (EM) bandgap structures and defected-ground-structure (DGS) approaches5 have also been applied to the design of UWB filters, but these approaches are difficult to integrate into planar systems.
The development of a high-performance UWB filter is an involved task that poses many challenges. A 110-percent fractional bandwidth requirement renders most typically used bandpass-filter design techniques useless. The required flat group delay over such a large passband and the FCC emissions limit at the low-frequency end also pose interesting design challenges for realizing a practical UWB bandpass filter.
In order to solve this design dilemma, the authors developed a simple topology that uses an open-circuit, quarter- wavelength resonator and sections of quarter-wavelength coupled lines instead of anti-parallel coupled lines as proposed by Hsieh and Wang.4 The shunt open-circuit resonator plays the role of a series inductive-capacitive (LC) resonator. As a result, the total filter assembly can be viewed as two shorted stubs coupled together with the transmission line. This structure generates a single transmission zero (TZ). To increase the filter's selectivity, tapped quarter-wavelength, SIRs are incorporated into the circuit to generate multiple transmission zeros. This design approach is cost effective and yields the desired performance over the bandwidth of interest.
In this planar filter design approach, the short-circuit stub produces a pair of transmission zeros at f = 0 and f = 2f0, where f0 is the midband frequency of the filter. In order to achieve transmission zeros at other frequencies, the short-circuited stub is replaced with two-section open-ended stubs. The two-section open circuit configuration produces a pair of transmission zeros, one in the lower stopband and the other in the upper stopband. Unfortunately, this approach significantly adds to the size of the filter circuit. However, this can be circumvented by coupling the anti-parallel lines together as shown in Fig. 1.
The impedance of the SIR resonator shown in Fig. 2 can be derived using standard transmission-line theory as follows:
where
Z1 = the characteristic impedance of the first cascaded section;
Z2 = the characteristic impedance of the second cascaded section;
θ 1 = the electrical length of the first cascaded section; and
θ2 = the electrical length of the second cascaded section (with θ1+ θ 2 = π ) .
If Zin = 0, the resonant frequency of the SIR can be determined by
where
A = the impedance ratio of the SIR, which is defined as
The resonance condition of the SIR can be adjusted by changing the width and length of the cascaded impedance sections Z1 and Z2 .Since the frequency deviation, f/f0, directly depends on A, frequency tuning is facilitated by adjusting A. For the example filter, the value of Z1 was taken as 54/70Ω and Z2 is taken as 39 Ω in order to achieve a passband compatible with the unlicensed UWB frequency range.
A filter was realized with microstrip on an alumina substrate with dielectric constant, er = 9.9, and thickness = 0.25 mm. The frequency response of the filter was simulated by using the Linmic 6.3 circuit simulation software from Computer Simulation Technology (www.cst.com) and the electromagnetic (EM) simulation tools within the Advanced Design System (ADS) suite of computer-aided-engineering (CAE) software simulation tools from Agilent Technologies (www. agilent.com). By meandering the output stub as shown in Fig. 3, it was possible to reduce the size of the filter assembly from 8.41 x 3.8 mm to 7.64 x 3.8 mm.
Continue to page 2
Page Title
Measurements on the planar filter were performed using a model E8361A Performance Network Analyzer (PNA) microwave vector network analyzer (VNA) from Agilent Technologies with frequency range of 10 MHz to 67 GHz. The VNA measurements showed good agreement with the computer-simulated performance predictions for both of the filter assemblies shown in Fig. 4.
The experimental broadband planar filters exhibit outstanding insertion loss of less than 1 dB, including the losses for coaxial connectors. They also feature flat group delay of less than 1 ns across the full operating band. The slight deviation between the measured and simulated performance at the higher frequencies is mainly due to the imprecise calibration and fabrication tolerances of the filter.
In summary, it was possible to achieve good UWB electrical characteristics while also maintaining a relatively small filter footprint, using shorted parallel coupled lines in a microstrip circuit configuration. Measurements of electrical performance for two experimental designs showed fairly close agreeement with computer-simulated performance predicted by two commercial CAE software tools. The SIR approach used in these experiments yielded a considerable reduction in size along with excellent filter selectivity compared to other reported bandpass filter topologies for UWB applications. The simple geometry, compact size, good RF performance, and ease of integration and compatibility with monolithic microwave integrated circuits (MMICs) makes this planar design approach an attractive option for filters in wireless and communication systems.
REFERENCES
1. A. Saito, H. Harada, and A. Nishikata, "Development of bandpass filter for UWB communication," IEEE Microwave Theory & Techniques Symposium (MTT-S) digest, 2003, pp. 76-80.
2. H. Ishida and K. Araki, "Design &Analysis of UWB bandpass filter," 2003 IEEE Topical Conference on Wireless Communication Technology, pp. 457-459.
3. J. Gao, K. Zhu, W. Menzel, and F. Bogelsawk, "Shortcircuited CPW multiple-mode resonator for UWB band pass filter," IEEE Microwave and Wireless Components Letters, Vol. 16, No. 3, March 2006, pp. 104-106.
4. W. Menzel, L. Zhu, K. Wu, and F. Bogelsack, "On the design of novel compact broad-band planar filters," IEEE Transactions On Microwave Theory & Techniques, Vol. MTT-51, No. 2, February 2003, pp. 364-370.
5. P. Mondal et al., "Compact UWB bandpass filter," IEEE Microwave and Wireless Components Letters, Vol. 17, No. 9, September 2007, pp. 643-645.
6. M-Y. Hseigh and S-M. Wang, "Compact and Wideband Microstrip Bandstop Filter," IEEE Microwave and Wireless Components Letters, Vol. 15, No. 7, July 2005.