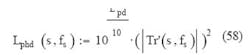Analyze Phase Noise In A Sampled PLL (Part 3)

Some have suggested that PLL noise degrades with frequency because the charge pumps are powered on for longer periods compared to the sampling period and therefore allow more noise to be transferred to the loop filter. In fact, the noise follows exactly what would be expected from FM theory and sampling theory. From FM theory, the noise is expected to increase by 6 dB for every doubling of frequency (20logf_s). However, from sampling theory, the noise power per Hz would be expected to decrease by 3 dB for every doubling of the sampling frequency (-10logf_s) since the noise power is now spread over twice the bandwidth. The net result is an increase in the phase noise by 3 dB for every doubling of the sampling frequency (10 logf_s).

With this in mind, take the phase noise at the phase detector due to the charge pumps, dividers, and other component, referenced to a 1-Hz bandwidth, to be equal to L_{pd_1Hz} = -207 dBc/Hz, with L_pd = 10log(fs) + L_{pd_1Hz} and, thus, L_pd = -163.021 dBc.

The loop acts on this noise to make a contribution to the overall sampled PLL noise as described by Eq. 58:

The plot in Fig. 18 below shows the difference between the output noise due to the phase detector for a continuous system and for a sampled system. There is a significant difference between the two. The apparent bandwidth for the sampled system is higher, and the noise at higher frequency offsets is 3 to 4 dB higher except at multiples of the sampling frequency where the contribution falls to zero.

In any PLL frequency synthesizer, the reference oscillator may also contribute to the overall phase noise close to the carrier. The SSB phase noise of the reference oscillator appears at the output of the synthesizer multiplied by the overall division ratio between the reference frequency and the output frequency.

Typically, for the type of VCTCXOs used as a reference source in a PLL synthesizer, the phase noise is flat from large frequency offsets to about 100 kHz from the carrier, then rises at a rate of about 10 dB/decade to about 400 Hz from the carrier, then rises at a rate of about 30 dB/decade. The reference oscillator phase noise may be modeled by defining the noise at three spot points and interpolating between those points (Fig. 19). For this analysis, points are chosen to be 1 MHz, 10 kHz, and 10 Hz, with (units in dBc and Hz, respectively) L_x0 = -155; f_x0 = 1 x 10⁶; L_x1 = -148; f_x1 = 10 x 10³; L_x3 = -90; and f_x3 = 10.

Then, the reference oscillator phase noise can be modeled by using Eq. 59.

Figure 20 shows the output phase noise due to the VCTCXO reference oscillator. Once the reference oscillator's phase noise has been modeled, it is possible to plot the effect the loop has on that phase-noise contribution to the overall PLL synthesizer. Usually, the reference noise is well below the contribution due to the phase detector or dividers except at low offset frequencies (typically below a few hundred Hz), as shown in Eqs. 60 and 61:

With models developed for the various noise sources in a sampled PLL, the multiple sources can be combined to create an overall noise model for the synthesizer. Each of these sources is modified by the PLL according to the equations below. For example, the noise generated by modulation of the VCO by thermal noise in the loop filter is shown in Eq. 62:

The noise due to the phase detector modified by the loop response is given in Eq. 63:

The noise of the free-running VCO as modified by the loop is represented by Eq. 64:

The noise from the reference oscillator as modified by the loop is represented by Eq. 65:

The combined output phase noise due to all the sources modified by the loop is shown in Eq. 66:

Figure 21 shows the overall predicted noise for the PLL and the contributions from some of the relevant phasenoise sources. Figure 22 shows the measured phase noise of the test PLL. Note that the close-in phase noise is higher than predicted by the simulation above. This is because the noise floor of the NTS1000A test system has been reached. The instrument's specification sheet lists its noise floor as -40 dBc/Hz offset 10 Hz from the carrier and -74 dBc/Hz offset 100 Hz from the carrier.

Figure 23 shows the same information plotted on a linear scale similar to what it might look like on a spectrum analyzer. This also allows closer inspection of the noise in the nulls that occur at the sampling frequency and its harmonics. In this analysis, it is also possible to make the oscillator noise higher than the reference/phasedetector/ divider noise to see the effects. In this new example, the far-out phase noise and close-in phase noise will be left unchanged but raise the level of the 20 dB/decade region will be raised by 20 dB, with the resulting parameters (in units in dBc and Hz, respectively) L₀ = -155; f₀ = 3 x 10⁶; L₂ = -108; f_x1 = 100 x 103; L3 = -70; and f₃ = 1x 10³.

Continue to page 2

Page Title

The plot in Fig. 24 shows the effect of the increase in oscillator noise.

Even though the oscillator noise is above the level of the other noise sources, the effects of sampling in the loop are evident at the harmonics of the sampling frequency.

In the plot of Fig. 25, the upper trace shows the measured effect of a relatively noisy oscillator. This is achieved by modulating the VCO with broadband noise to produce the effect of a noisy oscillator. The lower trace shows the normal performance of the PLL.

To continue the analysis, the phasedetector/ divider noise can be made significantly higher than the oscillator noise, at -153 dBc/Hz, to study the effect of the change. Figure 26 shows the effect of increasing the phase detector noise floor by 10 dB, in a plot of phase noise due to all sources. The same effect would be produced by a noisy reference divider or a noisy feedback divider. (In each case, the noise spectrum is assumed to be flat.)

The upper trace in Fig. 27 shows the measured phase noise when reference phase noise is raised by 10 dB by modulating the reference VCTCXO with pre-emphasized broadband noise (to produce flat phase noise sidebands on the reference signal). The lower trace shows normal PLL performance.

There are a number of simulation packages provided by PLL chip manufacturers such as ADIsimPLL from Analog Devices and EasyPLL from National Semiconductor. Although they may take discrete time effects into account for the prediction of transient responses, they only use a linear approximation for the loop response and phase noise predictions. For many applications, this simplification may be sufficient for a given design. But with the trend toward faster-settling-time PLLs where the loop bandwidth must be a significant fraction of the sampling frequency, something closer to the true response is required and the analysis presented in this multi-part article can provide a very close estimation of expected performance in sampled PLLs.