Meet the Challenge of Designing Electrically Small Antennas
Download this article as a .PDF
Antennas are vital for communications devices, although the continuing miniaturization of communications products has forced antenna designers to follow suit. However, due to the fundamental limitations in size and performance (Chu’s limit), achieving miniaturization with good antenna performance is challenging. Electrically small antennas (ESAs) are limited in bandwidth and radiating efficiency.
By understanding the effects of antenna size reduction on quality factor (Q), bandwidth, efficiency, and gain, it is possible to design a miniature antenna without drastically compromising performance. To demonstrate the effectiveness of this approach, an ESA was designed and developed for GPS (1.575 GHz) at one-tenth the operating wavelength. As will be shown, the Q of this proposed antenna design is closer to Chu’s limit that an equivalent-sized dipole or loop antenna.
Antenna sizes for many communications applications are mainly driven by customer requirements, and are generally much smaller than simple quarter-wavelength monopoles. Due to fundamental limitations, however, antennas can only be made so small without sacrificing tradeoffs in performance. Similarly, very compact antennas with ground planes too close to the radiating element suffer from certain performance issues.1 The tangential components of alternating current (AC) flowing on the antenna’s radiating surface tend to be nullified by the induced surface current on the ground plane.
Attempting to miniaturize an antenna by having radiating element(s) very close to the ground plane results in low radiation resistance, high reactance, narrow bandwidth, and poor radiation efficiency. The bandwidth capacity of a small antenna is approximately inversely related to the radiation quality factor (Q). Hence, antenna miniaturization is quite challenging. Metamaterials have been quite popular as far as antenna miniaturization is concerned.
These artificial structures can be engineered to support negative and zeroth-order modes which were not available in traditional microstrip antennas.2 In general, the frequencies of these resonances are lower than resonances obtained at positive modes and, thus, miniaturization is possible without sacrificing performance. However, metamaterial-based structures inherently have high Q and narrow bandwidth.3
Due to the small radiator size of miniaturized antennas, the available gain is usually quite low. Various antenna designs are available in the technical literature, but most suffer from negative gain (loss) and narrow bandwidths.4,5 Recently, a non-Foster circuit-based matching technique was introduced to overcome the fundamental limits in antenna miniaturization previously reported.6-8
To evaluate the challenges of designing ESAs, their performance parameters were studied and applied to the design of an ESA at the GPS frequency (1.575 GHz) using a split-ring resonator (SRR) which exhibits negative permeability. The methodology and layout of the antenna will be presented—and the performance of the antenna evaluated—to better understand the fundamental limits of an ESA.
The fundamental limit for electrically small antennas (ESAs) was addressed by Wheeler in 1947.9 It defined the maximum dimension of an ESA as being less than λ/2π. In 1948, Chu10 proposed that these small antennas have an inherent minimum value of Q. Since the lower limit of Q is inversely proportional to the electrical size of an antenna, it restricts the attainable impedance bandwidth for a given antenna size. McLean11 modified this earlier work on minimum antenna Q for a perfect lossless matching network, and proposed a new Q limit for a small linear antenna (QL) as
QL = 1/ka + 1/(ka)3 (1)
The results were in agreement with Chu.10 Also, the minimum Q for a circularly polarized ESA is given by Eq. 2:
QL = 0.5[(2/ka) + 1/(ka)3] (2)
where
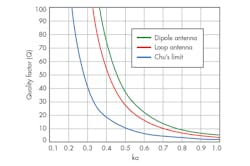
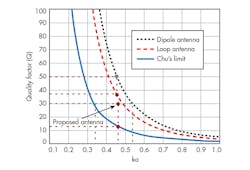
k = λ/2π and a = the radius of the sphere enclosing the antenna. Figure 1 depicts the relationship between Q and the electrical size of the antenna. The estimations of Q values for loop and dipole antennas are also plotted and are above the fundamental Chu’s limits for those antennas.
For the ESA, the antenna radiation Q is represented by Qa and the matching network Q is represented by Qm. Given certain assumptions, the efficiency of an antenna, ηa , can be expressed in terms of the efficiency of the matching network, ηm, as
ηa = ηm(1 + Qa/Qm) (3)
The efficiency of an antenna can be measured using the “Wheeler Cap” method in which a metallic “Wheeler Cap” with λ/2π radius covers the ESA, and the near-field reactive and radiated power is trapped within this cap. In a different measurement case, the radiated power propagating in free space is obtained without the cap. The efficiency is then estimated since the loss resistance can be separated from the radiation resistance in the post-processing of both test cases. The approximate normalized bandwidth (BW) for the maximum VSWR in terms of Q can be found by Eq. 4:
BW = (VSWR – 1)/[Q(VSWR)0.5] (4)
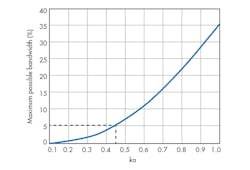
Figure 2 shows the maximum possible bandwidth that can be achieved by an ESA with respect to any change in electrical size. Since the radiating element is close to the ground plane, the radiation efficiency of an ESA is low, the energy stored in the near field increases, and the Q is high, resulting in a small impedance bandwidth. Also, the gain of an ESA is restricted according to the Harrington bound12 as
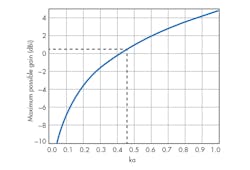
G(dBi) = 10log[(ka)2 +2(ka)] (5)
Figure 3 shows the variation in the gain bound with antenna size. For an ESA, ka < 1 and the maximum achievable gain is 3 dBi.
ESA Design Example
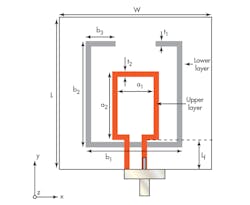
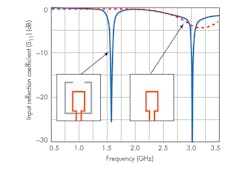
Figure 4 shows the circuit geometry of the proposed ESA. It consists of a square loop on the top circuit layer which is capacitively coupled to a rectangular split ring resonator (SRR) on the bottom circuit layer. The antenna was designed on 1.6-mm-thick FR-4 circuit material with a permittivity of 4.4 and loss tangent of 0.02. Figure 5 shows the impact of coupling the SRR and the loop antenna. The square loop structure attempts to resonate at 3.02 GHz but suffers from poor impedance matching. However, by including the SRR in the bottom circuit layer, not only are these reflections improved, but an additional resonance is achieved at 1.575 GHz (as shown in Fig. 5).
Figure 6 shows the surface current density of the proposed ESA. As can be seen, the current at 1.575 GHz is largely concentrated in the bottom layer due to the presence of the SRR. At the higher frequency (3.02 GHz), the current is mainly present in the square loop. The radius of the sphere that encloses the antenna is a = 13.9 mm.
Since the antenna is resonating at 1.575 GHz, the corresponding free-space wavelength, λ0, is 189.9 mm and the wavenumber, k, is 0.033 radians/mm. The value of ka is 0.457. Since the antenna is linearly polarized, using the McLean fundamental limit for calculating the minimum Q is
QL = (1/0.457) + 1/(0.457)3 = 12.25 (6)
The normalized bandwidth for a 2.0:1 VSWR can be estimated by the use of Eq. 7:
BW = 1/Q(2)0.5 = 5.77% (7)
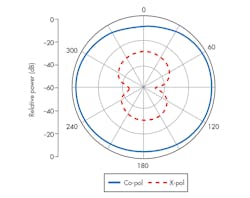
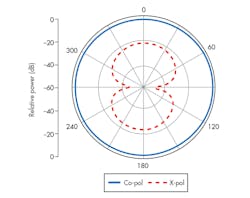
The maximum possible gain of the proposed antenna is calculated as 0.5 dBi. This is less than the directivity of a short dipole (e.g., 1.76 dBi). Figures 7 and 8 show the E- and H-plane radiation patterns, respectively, for the proposed antenna at 1.575 GHz. The radiation patterns are nearly omnidirectional, with low cross-polarization levels in both planes.
The designed metamaterial antenna exhibits a percentage impedance bandwidth of 2.35% at f0 = 1.58 GHz. This corresponds to a Q of 30, which is close to the minimum Q obtained from Chu’s limit, as shown in Fig. 2. Thus, the realized gain of the designed antenna is higher than the maximum gain bound (e.g., 0.5 dBi, by 0.22 dB), with a simulated radiation efficiency of 53.5%.
Figure 9 compares the Q of the proposed antenna with the fundamental limits for an ESA, loop antenna, and dipole antenna. For the same size, it can be seen that lower Q has been achieved for the ESA compared to the loop and dipole antennas. Also, for the same bandwidth, the electrical size of the proposed antenna is much smaller than the other antenna structures. This is worth noting because the design of small antennas for ka < 0.4 results in negative gain.
In summary, attempts to reduce the size of any antenna will yield certain performance tradeoffs because of fundamental design limits. However, it has been possible to develop a novel ESA with better Q and bandwidth compared to equivalent-sized standard dipole or loop antennas. The proposed ESA has ka = 0.457, 2.35% bandwidth, and Q = 30, which is still higher than the fundamental limit for an antenna of this small size.
Sameer Kumar Sharma, Researcher
Department of Electrical Engineering, Indian Institute of Technology Kanpur, Kanpur, India 208016
Deepak Singh Nagarkoti, Researcher
Isotropic Systems Ltd., London, United Kingdom
References
1. J. Sten, A. Hujanen, and P.K. Koivisto, “Quality factor of an electrically small antenna radiating close to a conducting plane,” IEEE Transactions on Antennas and Propagation, Vol. 45, No. 5, 2001, pp. 829-837.
2. S.K. Sharma, A. Gupta, and R.K. Chaudhary, “Epsilon negative CPW-fed zeroth-order resonating antenna with backed ground plane for extended bandwidth and miniaturization,” IEEE Transactions on Antennas and Propagation, Vol. 63, No. 11, 2015, pp. 5,197-5,203.
3. A. Li, K.M. K.. Leong, and T. Itoh, “Infinite wavelength resonant antennas with monopolar radiation pattern based on periodic structures,” IEEE Transactions on Antennas and Propagation, Vol. 55, No. 3, 2007, pp. 868-876.
4. S.K. Sharma and R.K. Chaudhary, “A compact zeroth-order resonating wideband antenna with dual-band characteristics,” IEEE Antennas and Wireless Propagation Letters, Vol. 14, 2015, pp. 1,670-1,672.
5. M.A. Abdalla, S. Karimian, and Z. Hu, “Dual band spurious-free sir metamaterial antenna,” 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, 2014 conference proceedings, pp. 1,005-1,006.
6. S. Sussman-Fort and R.M. Rudish, “Non-Foster impedance matching of electrically small antennas,” IEEE Transactions on Antennas and Propagation, Vol. 57, No. 8, 2009, pp. 2,230-2,241.
7. D.S. Nagarkoti, Y. Hao, D.P. Steenson, L. Li, E.H. Linfield, and K.Z. Rajab, “Design of broadband non-Foster circuits based on resonant tunneling diodes,” IEEE Antennas and Wireless Propagation Letters, Vol. 15, 2016, pp. 1,398-1,401.
8. J. Tian, D.S. Nagarkoti, K.Z. Rajab, and Y. Hao, “Graphene-based tunable non-Foster circuit for VHF applications,” AIP Advances, Vol. 6, No. 6, 2016, 065202.
9. H.A. Wheeler, “Fundamental limitations of small antennas,” Proceedings of IRE, Vol. 35, No. 12, 1947, pp. 1,479-1,484.
10. L.J. Chu, “Physical limitations of omni-directional antennas,” Journal of Applied Physics, Vol. 19, No. 12, 1948, pp. 1,163-1,175.
11. J.S. McLean, “A re-examination of the fundamental limits on the radiation Q of electrically small antennas,” IEEE Transactions on Antennas and Propagation, Vol. 44, No. 5, 1996, pp. 672-676.
12. R.F. Harrington, “Effect of antenna size on gain, bandwidth, and efficiency,” Journal of Research of the National Bureau of Standards-D Radio Propagation, Vol. 64D, No. 1, 1960, pp. 1-12.