Approach Trims Size Of Dipole Antennas
This file type includes high resolution graphics and schematics when applicable.
Dipole antennas can be reduced in size by means of a novel design technique. The approach adds two short-circuited cylindrical covers to the extremes of what would have been conventional dipole arms. The increased inductive load reduces the antenna’s resonant frequency without compromising the radiation pattern.
Related Articles
• Low-Cost Substrate Supports Multiband Patch Antenna
• Active Antenna Systems Enjoy Growth
• Save Space with a Luna-Slot Antenna
To demonstrate this approach, the resonant frequency of a dipole antenna was reduced by 35% (the technique can reduce resonant frequency by as much as 64% if bandwidth requirements are reduced). As the experimental results show, the wire size of the antenna can also be reduced to bring about the resonant-frequency reduction, without folding or resorting to circuit materials with high dielectric permittivity. All of these factors indicate an antenna design approach suitable for practical applications.
As is well known, the properties of electrically short cylindrical dipole, monopole, and whip antennas can be improved by adding inductive loads to these structures. This is particularly useful for applications where antenna size must be minimized. The effects of series inductive loads have been presented in a number of studies.
For example, by superposition of asymmetrical dipoles, one researcher determined the resulting efficiency of a short monopole for various locations of the load.1 Another researcher built upon this work by developing an approximate solution for the current distribution on doubly loaded short antennas, and computing the impedences and radiation patterns.2 By using a piecewise sinusoidal moment method, yet another researcher computed the radiation resistance improvement and the load point for maximum efficiency.3,4 Since then, a number of studies have been performed on the benefits of inductively loaded antennas.5-13
As noted above, this report details a novel approach for reducing the size of a dipole antenna by adding a distributed inductive load. The load consists of a short-circuited cylindrical cover with less than one-quarter-wavelength overall electrical length. Of course, it is useful to know the effects of the load on various antenna parameters, including bandwidth, radiation pattern, and input impedance; various parameters for this modified antenna will be compared to a conventional dipole.
Good agreement was achieved between the measurements and computer simulations. Both sets of results show that the antenna can exhibit one-half-wavelength dipole characteristics with reduced size.
Theoretical Analysis
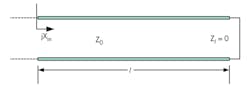
Generally, the input impedance of a one-half-wavelength dipole is capacitive below its resonant frequency. Any attempt to reduce the resonant frequency of the dipole antenna must therefore add an inductive load in such a manner that the capacitive impedance of the dipole is exactly canceled at the reduced resonant frequency. According to transmission-line theory (TLT), an inductive load could consist of a short-circuited transmission line with overall length less than one-quarter wavelength, with reactance as given in Eq. 1:
jXin = jZ0tanβl (1)
where:
l = the length of the short-circuited transmission line;
β = the phase-shift constant of the short-circuited transmission line; and
Z0 = the characteristic impedance of the short-circuited transmission line.
Since this transmission line is considered short, the losses in this model are assumed to be negligible; they are not taken into account and the attenuation constant is set to zero. Therefore, this configuration can modeled as a short-circuited lossless transmission line as depicted in Fig. 1.
Also based on TLT, the impedance of the dipole can be seen approximately as an input impedance of lossy open-circuit transmission lines. As a result, the reactance of the dipole can be expressed in terms of Eq. 2:
jX′in = (-jZ′0)[(α′/β′)sh(2α′l′) + sin(2β′l′)]/[ch(2α′l′) – cos(2β′l′)] (2)
where:
α′ = the equivalent attenuation constant of the dipole;
β′ = the equivalent phase-shift constant of the dipole;
Z0′ = the characteristic impedance of the dipole; and
l′ = the length of the dipole arm. When l′ < 0.35λ, Eq. 2 can be simplified to Eq. 3:
jX′in = -jZ′0cotβ′l′ (3)
This file type includes high resolution graphics and schematics when applicable.
Reducing The Dipole
This file type includes high resolution graphics and schematics when applicable.
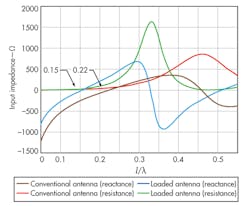
From Eqs. 1 and 3, the signs of the reactance of the dipole and the short-circuited transmission line are opposite, and the capacitive impedance of the dipoles could be exactly cancelled by the short-circuited microstrip line at the reduced resonant frequency by properly selecting the values of l and l′. With the aid of the High-Frequency Structure Simulator (HFSS) software from ANSYS, the simulated input impedance of an inductively loaded dipole and a conventional dipole are shown in Fig. 2.
As can be seen in this figure, the resonance of a loaded dipole is 1/λ = 0.15 while the resonance of a conventional antenna is 1/λ = 0.22. Therefore, the effective length of the loaded dipole is increased. It also can be seen that the additional inductance offered by the inductive loads compensates for the increased capacitance of the dipole at a lower resonant frequency. According to previous results, the use of an inductive load can effectively reduce the size of the antenna.
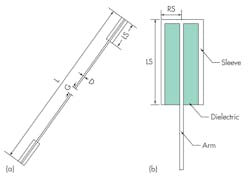
To reduce the size of the dipole, two inductive loads consisting of a short-circuited cylindrical cover or sleeve were added to the top of the upper and lower arms, with the dipole extremities touching the inner edges of the sleeves. Figure 3(a) shows the geometry of this loaded dipole, with the transversal of the sleeve in Fig. 3(b). The total length (L) of the structure is 31.6 mm, with the upper and lower arms of the loaded dipole connected to the inner and outer conductors, respectively, of a coaxial feed through a quarter-wave balun.
The gap (G) between the upper and lower arms is 0.6 mm. The diameter of the dipole conductor (D) is 1 mm. The sleeve positions are selected near the extremities of the dipole arms to take into account the current distribution on the dipole. Since the dipole current is at its maximum at the center, placing the sleeves near the dipole central region would cause more disturbance to the dipole current in this region. As such, the matching-element sleeves are positioned near the dipole ends for minimal interference to the dipole current.
The current on the dipole excites the sleeves to induce a magnetic field in the near-field region and in the extremities of the antenna, contributing to inductively stored energy. This compensates for the near-field capacitive effect generated by the electric field produced by the dipole current. To better understand the behavior of the loaded dipole, it will be compared to a conventional dipole design with total length of 31.6 mm and diameter of 1 mm [Fig. 3(a)] in all simulations.
It can be useful to explore how different sleeve materials can affect antenna performance. This can be accomplished by investigating the individual resonant effects based on the relative permittivity of the dielectric material (εr), the radius of the sleeve (RS), and the length of the sleeve (LS).
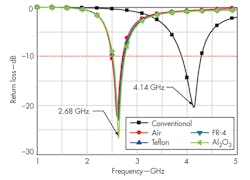
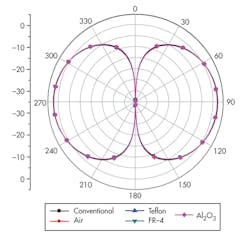
For comparison, four different materials were filled into the sleeve, including air (εr = 1), Teflon (εr = 2.2), FR-4 (εr = 4.4), and Al2O3 (εr = 9.8). In this case, RS = 2 mm and LS = 4 mm. Figure 4 shows simulated return losses with the different dielectric materials for comparison.
While the resonant frequency of a conventional dipole antenna (the reference) might be around 4.14 GHz, similar dipole structures loaded with different materials resonate at around 2.68 GHz, or a reduction in resonance frequency of 35.5% relative to the reference. As Fig. 4 indicates, different materials filled into the sleeve can reduce the resonant frequency slightly. This may be due to the distributed inductance per unit length of the coaxial line, which consists of the sleeve and dipole arm, and is independent of the value of εr. The distributed inductance is given by Eq. 4:
L = (μ/2π)[ln(b/a)](H/m) (4)
where:
a = the inner radius of the coaxial line; and
b = the outer radius of the coaxial line.
The unit-length inductance of the sleeve is determined by the length and radius of the sleeve, rather than on the material permittivity, εr.
This file type includes high resolution graphics and schematics when applicable.
Comparing Radiation Patterns
This file type includes high resolution graphics and schematics when applicable.
Figure 5 compares radiation patterns of a conventional dipole and a dipole loaded with different materials. The radiation patterns are similar to that of a half-wavelength dipole, showing that the loading sleeves do not alter the radiation pattern. Simulations show maximum gain of about 2.2 dBi for the modified antennas, compared to about 2.52 dBi for the conventional dipole reference. This can be attributed to a change in surface current direction. This presents the possibility of reduced radiation field and, as a result, diminished antenna gain. This is one tradeoff that comes with achieving a smaller antenna design.
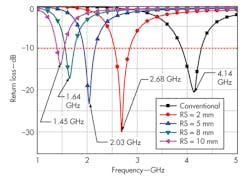
The antenna parameter related to the radius of the sleeve (RS) can impact the resonant frequency of the loaded dipole. Figure 6 compares loaded and unloaded dipoles, with considerably different resonant frequencies. By Eq. 4 and Fig. 2, as the distributed inductance per unit length of the sleeve is increasing, the resonant frequency shifts towards a lower frequency. Reductions of 35% and 64% in resonant frequency are achieved for RS values of 2 and 10 mm, respectively.
The 10-dB bandwidths of the unloaded and loaded dipoles with different RS values were also simulated at frequencies of 0.38, 0.35, 0.22, 0.17, and 0.14 GHz. A degradation in impedance matching was found in proportion to increasing RS value. This degradation in bandwidth and impedance matching may best be explained by the increase in distributed inductance. As Fig. 2 shows, the slope of the input inductance curve is increasing with increasing RS value, leading to the difficulty in impedance matching.
As Fig. 5 shows, the E-plane radiation patterns for the different loaded dipoles are similar, and the radiation characteristics are not affected by the loaded versus unloaded dipoles. The simulations indicate peak gain of about 2.34 dBi for the loaded dipoles and 2.52 dBi for the unloaded dipole in comparison.
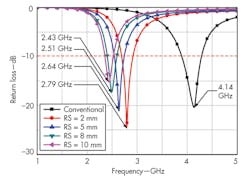
Figure 7 shows the effects of changing the sleeve length (LS) while the dipole length, wire radius, and filler material are constant, with RS = 2 mm. It can be seen that the reduction in resonant frequency is greatly dependent upon the different LS values. The changes in LS value had minimal effect on radiation patterns, either for loaded or unloaded dipoles. The simulated peak gain of the loaded dipole with different LS values is around 2.16 dBi compared with 2.52 dBi for the unloaded dipole.
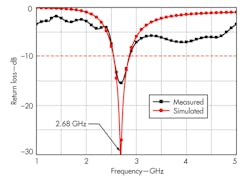
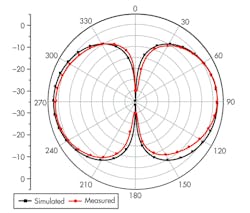
After completing a parametric optimization, an experimental dipole was fabricated with RS = 2 mm and LS = 4 mm. The antenna’s performance was measured in an anechoic chamber, using a far-field antenna measurement system and model E8362C vector network analyzer (VNA) from Agilent Technologies. The measured and simulated return-loss performance levels and radiation patterns of the loaded dipole are shown in Figs. 8 and 9, respectively, where measured and simulated results agree quite closely. Deviations of the impedance matching dip may be due to fabrication tolerances and measurement imprecision.
B. Gong, Doctor
L.S. Su, Doctor
Q.R. Zheng, Doctor
Institute of Information and Navigation, Air Force Engineering University, Xi’an, Shaanxi, 710077, People’s Republic of China
Y.Z. Yin, Professor
X.S. Ren, Doctor
National Key Laboratory of Science and Technology on Antennas and Microwaves, Xidian University, Xi’an, Shaanxi, 710071, People’s Republic of China
This file type includes high resolution graphics and schematics when applicable.
References
This file type includes high resolution graphics and schematics when applicable.
1. C.W. Harrison, “Monopole with inductive loading,” IEEE Transactions on Antennas & Propagation, Vol. AP-11, July 1963, pp. 394-400.
2. J.C. Lin, D.P. Nyquist, and K.M. Chen, “Short cylindrical antennas with enhanced radiation or high directivity,” IEEE Transactions on Antennas & Propagation, Vol. AP-18, No. 4, July 1970, pp. 576-580.
3. R.C. Hansen, “Efficiency transition point for inductively loaded monopole,” Electronic Letters, Vol. 9, No. 5, March 8, 1973, pp. 117-118.
4. R.C. Hansen, “Optimum inductive loading of short whip antennas,” IEEE Transactions on Vehicular Technology, Vol. VT-24, No. 2, May 1975, pp. 21-29.
5. E.G. Korkontzil, P.C. Liakou, D.P. Carraasco, and C. Reig, “Dual frequency patch antenna, reduced in size by use of triangularly arranged peripheral slits,” in Proceedings of the First European Conference on Antennas and Propagation (EuCAP 2006), 2006, pp. 1-6.
6. J.A. Tirado-Mendez, H. Jardon-Aguilar, F. Iturbide-Sanchez, I. Garcia-Ruiz, V. Molina, and R. Acevo-Herrera, “A proposed defected microstrip structure (DMS) behavior for reducing rectangular patch antenna size,” Microwave & Optical Technology Letters, Vol. 43, No. 6, December 2004, pp. 481-484.
7. A. Pomerleau and M. Fournier, “Inductively Loaded Monopole,” Antennas and Propagation Society International Symposium, Vol. 10, December 1972, pp. 81-84.
8. W. Czerwinski, “On Optimizing Efficiency and Bandwidth of Inductively Loaded Antennas,” IEEE Transactions on Antenna and Propagation, Vol. 13, No. 5, September 1965, pp. 811-812.
Related Articles
• Low-Cost Substrate Supports Multiband Patch Antenna
• Active Antenna Systems Enjoy Growth
• Save Space with a Luna-Slot Antenna
9. R. Hansen, “Efficiency and Matching Tradeoffs for Inductively Loaded Short Antennas,” IEEE Transactions on Communications, Vol. 23, No. 4, April 1975, pp. 430-435.
10. M. Fournier and A. Pomerleau, “Experimental Study of An Inductively Loaded Short Monopole Antenna,” IEEE Transactions on Vehicular Technology, Vol. 27, No. 1, February 1978, pp. 1-6.
11. R.C. Hansen, “Efficiency Transition Point for Inductively Loaded Monopole,” Electronics Letters, Vol. 9, No. 5, March 1973, pp. 117-118.
12. B.A. Kramer, C.C. Chen, and J.L. Volakis, “Optimization of an Inductively Loaded Log-Spiral Antenna,” Antennas and Propagation Society International Symposium, June 2007, pp. 2993-2996.
13. M.S. Ruiz-Palacios and M.J. Martinez-Silva, “Inductively loaded shorted patch antenna with reduced size,” Antennas & Propagation Conference, 2009, LAPC 2009, Loughborough, November 2009, pp. 765-768.
This file type includes high resolution graphics and schematics when applicable.