This file type includes high resolution graphics and schematics when applicable.
Magnetic resonance imaging (MRI) is a powerful tool for medical research—specifically, for studying the condition of internal organs in humans and animals. To construct an MRI probe for animal research, the characteristics of a transverse-electromagnetic (TEM) coil were analyzed and optimized using computer simulation software and method-of-moments (MoM) computer simulation approaches. An effective model for the MRI design was developed that optimizes the frequency response of the MRI probe at 433 MHz.
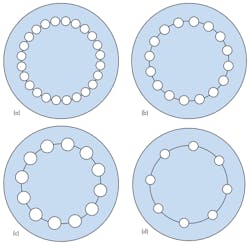
The MRI probe was designed using n-element coupled coaxial lines, with n = 24, 16, 12, and 8. As a reference, the MRI probe design was compared to the shielded birdcage TEM resonators commonly used for MRI probes. Numerical calculations for the probe were carried out using the MoM approach with LINPAR for Windows [Matrix Parameters for Multiconductor Transmission Lines (MTL)] two-dimensional (2D) analysis software. It was used to perform numerical evaluation of the quasistatic matrices ([L], [C], [R], and [G]) representing the multiconductor transmission lines forming the MRI probe.
The S11 response of the MRI probe was optimized for 433 MHz using software tools based on MTL with MatLab from MathWorks mathematical analysis software. The approach permitted evaluation of the probe’s unloaded quality factor (Q). The impact of such parameters as the radius of the coaxial transmission lines (TLs) and the numbers of elements were studied in the analysis.
An RF coil is an essential component in an MRI system. Many different types of RF coils have been developed for MRI, with each generation offering some performance improvements. Prior to the introduction of the TEM resonator in 1994,1 the birdcage resonator was the most widely used type of RF coil for MRI probes.2 A TEM resonator has several advantages over a birdcage coil, including improved excitation field homogeneity, high quality factor (Q), and ease of tuning.3-5 The first descriptions of TEM resonator structures appeared in several patents which provided descriptions of TEM resonator structures.6,7
Other published work on TEM resonators focused on modeling the resonators using TL concepts. In one approach, the resonator consisted of a section of coaxial TL terminated by capacitors.1 A lumped-element approach with conductors operating as inductors with mutual coupling and capacitors was used for modeling a TEM resonator at 143 MHz.8 In addition, a simplified coupled TL model of a TEM resonator was developed.9,10 Using the boundary element method (BEM), researchers developed a 12-element lumped-element TEM resonator model at 200 MHz. It should be noted that this model is invalid at higher frequencies.11
In previous work by the current authors,12 a numerical tool was demonstrated based on finite element method (FEM). Its purpose was to analyze an eight-element unloaded coaxial line transverse electromagnetic (TEM) resonator and design an MRI-probe for studies at 4.7 T. That MRI probe has -62.81 dB minimum reflection and Q of 260 at approximately 200 MHz.
To build upon that work, the current studies describe a model for multiple-conductor TLs transmission lines. This includes the exact calculation of the primary parameter matrices ([L] and [C]) from of ref. 12, adapted to full potential using MoM via a LINPAR for MS Windows analysis environment.13 The current reported efforts were applied to characterize the behavior of a TEM resonator at a Larmor frequency of 433 MHz for a high-Q (20-dB) MRI probe. A probe was designed and developed by varying the number and the radius of the n-elements coupled coaxial lines (n = 24, 16, 12, 8), used to form the MRI probe.
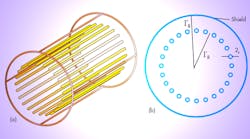
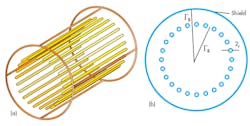
Figure 1 shows a TEM resonator. It consists of a number (n) of inner circular conductors (coaxial lines) distributed in a cylindrical pattern (2rR) in a particular diameter and connected with capacitors to a cylindrical outer shield of 2rB diameter.11,12 The length of the resonator is sized with respect to the wavelength (of 433 MHz) in free space, λ0 = 17.32 cm. To evaluate the [L] and [C] matrices in a LINPAR environment, it was necessary to estimate the cross section of the MRI resonator and all relevant dielectric characteristics using general programs in PASCAL. Figure 2 shows the segmentation of the charged surfaces of the n-element coupled coaxial MRI resonator using LINPAR for WINDOWS software.
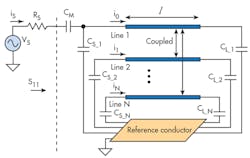
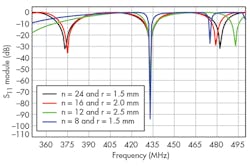
Numerical analysis was performed (Fig. 2) to determine the electromagnetic (EM) parameters for the [L] and [C] matrices of the TEM resonator. Once these parameters were calculated, it was possible to estimate the resonance spectrum (S11 response) of the MRI probe based on a TLM approach (Fig. 3).14 The MRI probe consists of shielded coupled coaxial lines with length l, matching capacitor (CM), and terminating capacitors CSi and CLi (where i = 1…n) (Fig. 3). The unloaded quality factor (Q = -20 dB) of the MRI system can be deduced from a reflection parameter (S11) sweep with frequency11,12:
Q-20 dB = fr/( fu - fl) (1)
where
fr = the resonance frequency of the probe,
fu = the -20-dB upper frequency limit of the probe, and
fl = the -20-dB lower frequency limit of the probe.
Based on previous work using the MoM approach, f,15-17 a software program was created to calculate the EM parameters of the MRI probe using n-element coupled coaxial lines. Every parameter is strongly dependent upon the resonator features and properties of the sample. Simulations conducted with this software indicate whether fabrication of a particular MRI probe design will be practical.
To design high-Q probes operating at 433 MHz, the structure of Fig. 2 was studied with n inner circular conductors (n = 24, 16, 12, 8) and coaxial radius r, and having the following geometric parameters:
Outer cylinder radius, rB, of 52.5 mm;
Inner cylinder radius, rR, of 36.25 mm;
Conductivity, σ, of 5.8 × 107 Σ/m; and
Relative dielectric constant, εr, of unity (1).
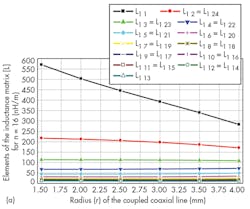
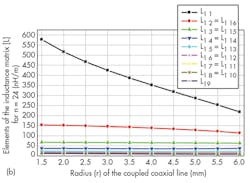
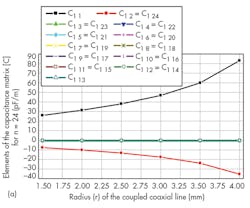
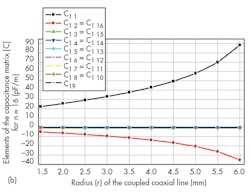
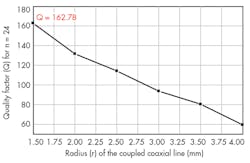
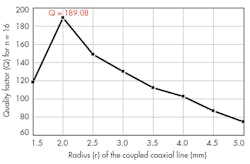
Figures 4 and 5 show the impact of r values for the probe’s circular conductors on the values of the elements of the inductance matrix and on the values of the elements of the capacitance matrix of the TEM-resonator for 24- and 16-element coupled coaxial lines, respectively. Figures 6 and 7 shows variations of Q (-20 dB) for n = 24 and n = 16, as calculated by Eq. 1.
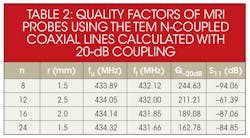
It appears that each of the two 24- and 16-element coupled coaxial MRI probe presents a higher Q (-20 dB) value for r = 1.5 mm and 2.0 mm, respectively. Similarly, a study was made of the influence of r on the Q of TEM MRI probes with 12- and 8-element coupled coaxial lines. The highest Q (-20 dB) value was found for n = 12 for a radius (r) of 2.5 mm. The highest Q (-20 dB) value for an n = 12 probe was found for a radius (r) of 1.5 mm.
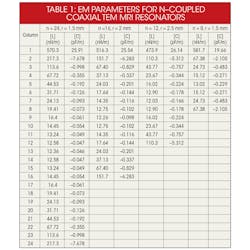
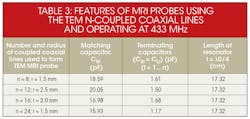
Tables 1 and 2 provide results for MRI probes designed and fabricated for use in the Industrial-Scientific-Medical (ISM) band at 433 MHz. Table 1 contains the values required to construct for a probe’s [L] and [C] matrices.11,12,18 In addition to Table 1, Table 3 contains features for optimum MRI probe configurations operating at 433 MHz with n-element coupled coaxial lines (where n = 24, 16, 12, 8) based on the design configuration of Fig. 3.
In summary, these studies have revealed the impact of the number of coupled lines and the radius of the probe structure on achieving high-Q performance with a TEM MRI probe structure. Optimization was performed by varying the number of elements and the radius of the structure. It was found that for a TEM MRI probe with 8-element coupled coaxial lines and radius, r, of 1.5 mm, a matching capacitor (CM) of 18.59 pF and terminating capacitors C{SUBSCRIPT Si} and CLi—both with value of 1.61 pF, minimum reflection of -94.06 dB and Q of 244.63—were measured. The design and analysis approach made it possible to optimize high-Q TEM MRI probes for use in the ISM band at 433 MHz.
Fatima Seghira, Engineer
Nadia Benabdallah, Doctor
Nasreddine Benahmed, Doctor
University of Tlemcen, P.O. Box 119, (13000) Tlemcen, Algeria
References
1. J.T. Vaughan, H.P. Hetherington, J.O. Out, J.W. Pan, and G.M. Pohost, “High frequency volume coils for clinical NMR imaging and spectroscopy,” Magnetic Resonance in Medicine, Vol. 32, 1994, pp. 206-218.
2. C.E. Hayes, W. A. Edelstein, J.F. Schenck, O.M. Mueller, and M. Eash, “An efficient highly homogeneous radio-frequency coil for whole-body NMR imaging at 1.5 T,” Journal of Magnetic Resonance Vol. 63, 1985, pp. 622-8.
3. T.S. Ibrahim, “Design of radio-frequency coils for magnetic resonance imaging applications: A computational electromagnetic approach,” doctoral dissertation, The Ohio State University, Columbus, OH, 2002.
4. G. Adriany, J.T. Vaughan, P. Andersen, H. Merkle, M. Garwood, and K. Ugurbil, “Comparison between head volume coils at high field,” in Proceedings of the 3rd SMR and 12th ESMRMB annual meeting, Nice, France, 1995, p. 971.
5. J.W. Pan, J.T. Vaughan, R.I. Kuzniecky, G.M. Pohost, and H.P. Hetherington, “High resolution neuroimaging at 4.1 T,” Magnetic Resonance Imaging, Vol. 13, 1995, pp. 915-921.
6. P. Röschmann, “High-frequency coil system for a magnetic resonance imaging apparatus,” U.S. Patent No. 4,746,866, 1988.
7. J.F. Bridges, “Cavity resonator with improved magnetic field uniformity for high frequency operation and reduced dielectric heating in NMR imaging devices,” U. S. Patent No. 4,751,464, 1988.
8. J. Tropp, “Mutual inductance in the birdcage resonator,” Journal of Magnetic Resonance, Vol. 126, 1997, pp. 9-17.
9. P. Röschmann, “Analysis of mode spectra in cylindrical N-conductor transmission line resonators with expansion to low-, high- and band-pass birdcage structures,” in Proceedings of the 3rd Annual Meeting of the International Society of Magnetic Resonance in Medicine, Nice, France, 1995. p.1000.
10. G.C. Chingas and N. Zhang, “Design strategy for TEM high field resonators,” in Proceedings of the 4th Annual Meeting of the International Society of Magnetic Resonance in Medicine, New York, NY, 1996. p. 1,426.
11. G. Bogdanov and R. Ludwig, “A Coupled microstrip line transverse electromagnetic resonator model for high-field magnetic resonance imaging,” Magnetic Resonance in Medicine, Vol. 47, 2002, pp. 579-593.
12. N. Benahmed, M. Feham, and M. Khelif, “Analysis and design of a coupled coaxial line TEM resonator for magnetic resonance imaging,” Journal of Physics in Medicine and Biology, Vol. 51, 2006, pp. 2093-2099.
13. A.R. Djordjevic, M.B. Bazdar, and T.K. Sarkan, LINPAR for Windows: Matrix parameters of multiconductor transmission lines, Software and user’s manual, Artech House, Norwood, MA, 1999.
14. R. Bouhmidi, N. Benahmed, N. Benabdallah, K. Aliane, S.M. Meriah, and F.T. Bendimerad, “Optimization of a Transverse Electromagnetic Resonator for Magnetic Resonance Imaging at High Field of 9.4 T,” 2012 Spring World Congress on Engineering and Technology (SCET), 2012.
15. N. Benabdallah, N. Benahmed, and B. Benyoucef, “Analyzing a resonator for MRI applications,” Microwaves & RF, Vol. 46, No 11, 2007, pp.92-98.
16. N. Benabdallah, N. Benahmed, B. Benyoucef, R. Bouhmidi, and M. Khelif, “EM analysis of the slotted-tube resonator with circular cross section for MRI applications,” Journal of Physics in Medicine and Biology, Vol. 52, 2007, pp. 4943-4952.
17. K. Aliane, N. Benahmed, N. Benabdallah, F.T. Bendimerad, and A. Benkaddour, “Resonators Support UHF MRI Systems,” Microwaves & RF, Vol. 51, No. 4, pp. 84-92, 2012.
18. R. Bouhmidi, N. Benabdallah, N. Benahmed, and M. Khelif, “Design coupled microstrip resonators for MRI,” Microwaves & RF, Vol. 46, No. 3, 2007, pp. 59-66.
This file type includes high resolution graphics and schematics when applicable.