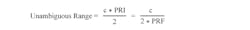Download this article in PDF format.
Radar, which is an acronym for radio detection and ranging, has a history that dates all the way back to the early part of the 20th century. Radar technology was originally developed for military services and was later utilized in combat in World War II. Since its early days, radar technology has significantly changed. Today, radar is used not only for military applications, but also for many civilian applications.
As stated, radar technology was originally developed for military purposes. Today, military services still represent the main area of usage for radar technology, as military applications on land, in the air, and at sea rely on radar. Among these applications are threat detection, missile guidance, air and marine navigation, and more.
Although radar technology has changed over time, its general concept remains the same. A typical radar system consists of both a transmitter and a receiver. The purpose of the transmitter is to transmit a signal in the direction of a target object. This signal must be strong enough to reach the location of the intended target, which could be located a long distance away from the transmitter.
When the transmitted signal reaches the target, a portion of that signal is reflected and then detected by the radar receiver. This reflected signal is also known as an echo. To successfully detect long-range targets, the radar receiver must be highly sensitive. Various types of information concerning the target can be obtained once the receiver detects the reflected signal. This information includes the size, distance, position, and speed of the target. Figure 1 illustrates a basic radar system.
1. This depicts the operation of a typical radar system.
Radar applications operate at various frequency bands. The table presents a list of different radar frequency bands.
The Radar Equation
The detected signal at the receiver input is obviously significantly weaker than the transmitted signal. The power level of this received signal is determined by several factors. It can be mathematically defined by the following equation (also known as the radar equation):
where:
Pt = transmitted power
G = gain of the antenna
λ = wavelength of the transmitted signal
σ = radar cross section
R = range (distance) between the antenna and the target
This equation implies that the same antenna is used for transmitting and receiving. This type of system is known as a monostatic radar system, which is commonly implemented. A bistatic radar system uses separate antennas for transmitting and receiving.
When a transmitted signal strikes a target, energy is scattered in various directions. Some of that energy is reradiated back to the radar system. The radar cross section (RCS) is an important radar parameter, as it determines the amount of energy reflected from a target. RCS is often described in mathematical terms as m2.
As mentioned, a radar receiver must be very sensitive so that it can detect signals that are reflected from targets at long range. Since all receivers generate some amount of noise, signal-to-noise ratio (SNR) is degraded as a signal passes through a receiver. Successfully detecting reflected signals requires a minimum SNR at the receiver output.
The minimum SNR corresponds to the minimum power level of a signal that can be applied to the receiver’s input for proper detection. If this minimum power level is known, the radar equation can be rearranged to determine the radar system’s maximum range. This equation is defined as follows:
where:
Pmin = minimum power level at the receiver input
It should be stated the equation shown for maximum target range describes radar performance in simplified terms. Other factors, such as propagation effects, can also affect performance.
Determining Range and Radial Velocity
Range is determined by the time needed for a transmitted signal to travel to the target and then back to the receiver. The radial velocity of the target is related to what is known as the Doppler shift. Essentially, a moving target will result in a returned signal with a frequency that is different than the frequency of the transmitted signal. This frequency, known as the Doppler frequency (fd), can be defined by the following equation:
where:
v = radial velocity of the target;
fo = frequency of the transmitted signal;
c = speed of light.
A positive Doppler frequency indicates an approaching target, while a negative Doppler frequency indicates a target that is moving away from the radar system. Thus, the frequency of the received signal is equal to the frequency of the transmitted signal plus the Doppler frequency if the target is approaching the radar system. The frequency of the received signal is equal to the frequency of the transmitted signal minus the Doppler frequency in the case of a target moving away from the radar.
Continuous-Wave Radar Signals
Radar systems that transmit continuous-wave (CW) signals can determine the velocity of a target. The velocity is determined due to the Doppler frequency. Although a CW-based radar system can determine target velocity, it cannot obtain information concerning the target’s range because of its lack of a timing reference.
In contrast to CW signals, a radar system that utilizes frequency-modulated-continuous-wave (FMCW) signals can determine a target’s velocity and range. An FMCW signal is essentially a waveform with a frequency that changes. Thus, utilizing an FMCW signal enables a target’s range and velocity to be determined.
Pulsed Radar Signals
Pulsed RF signals are the more common form of signals used in radar applications. A pulsed RF signal can be described as periodic bursts of RF energy, as the signal is essentially turned “on” for a certain amount of time and then turned “off” for another period of time.
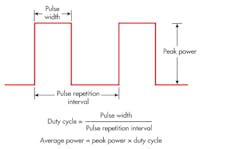
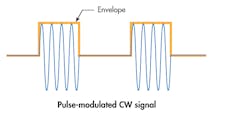
Figure 2 shows an ideal pulse, while Figure 3 shows an ideal pulsed RF signal. Pulses are defined by a number of characteristics, such as peak power, average power, pulse repetition frequency (PRF), pulse repetition interval (PRI), pulse width, duty cycle, rise time, and fall time. These pulse characteristics are important in regard to the performance of the radar system itself.
2. Shown above is an ideal pulse.
3. A pulse-modulated RF signal is commonly used in radar applications.
The PRF is the rate at which pulses are generated. The PRI, which is inversely related to the PRF, can be described as the time interval between pulses. One important radar parameter is the maximum unambiguous range, which is determined by the PRI. The maximum unambiguous range can be defined as the maximum distance a pulse can travel to reach a target such that the echo is received before the next pulse is transmitted. A target that is located beyond this distance can result in an obscured echo response because new pulses are transmitted before previously transmitted pulses are reflected back to the receiver. Thus, increasing the PRI increases the unambiguous range, which is mathematically defined by the following equation:
where:
c = speed of light
Resolution is another important radar parameter. Resolution determines how well a radar system can differentiate between two separate targets. In other words, two targets that are close to one another could be located at some distance away from the radar system. A radar system with sufficient resolution will be able to distinguish one target from the other. However, if the resolution is insufficient, the radar system would mistakenly only see one target instead of correctly seeing two separate targets.
Decreasing the pulse width of the transmitted signal enhances the resolution of the radar system. However, decreasing the pulse width also places limitations with respect to the amount of power that can be transmitted, thus restricting the radar system’s range. Longer range can be achieved by increasing the pulse width of the transmitted signal. Thus, an important tradeoff exists in terms of radar performance, as short pulses allow for better resolution, while long pulses allow for longer range.
Pulse Compression
Pulse compression is a technique that can be utilized to overcome the tradeoff between range and resolution. Pulse compression enables long pulses to be transmitted and then compressed at the receiver, thereby allowing a radar system to simultaneously achieve long range and high resolution. Pulse compression can be achieved by employing different modulation techniques.
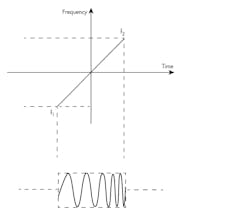
One pulse compression technique is based on linear frequency modulation (LFM) (Fig. 4). With this technique, a pulse begins with a certain RF carrier frequency and then linearly ramps in frequency throughout the entire duration of the pulse. Matched filtering at the receiver is responsible for compressing the received signal. LFM pulses are also known as FM chirps. Furthermore, another pulse compression technique is based on nonlinear frequency modulation (NLFM).
4. Shown is the LFM method for pulse compression.
Pulse compression can also be based on phase modulation. One technique employs binary phase shift keying (BPSK) modulation, using what is known as a Barker code sequence. This method can be used to create compressible pulses.
Antennas and Phased-Array Systems
One aspect of a radar system that has yet to be discussed in detail is the antenna. Proper antenna performance is critical for any radar system. The radar equation, which was presented earlier, shows how the performance of a radar system depends on the antenna’s gain. A larger antenna gain allows the radar system to achieve longer range. Furthermore, narrowing the antenna’s beamwidth increases its gain.
In radar applications, antenna beams are typically steered dynamically in order to cover the entire area of interest. This dynamic beam steering is utilized because a static beam would not have the capability to cover the entire area. Traditionally, steerable beams were accomplished by using mechanical positioning systems. However, modern radar systems often utilize phased-array antenna systems to electronically steer beams.
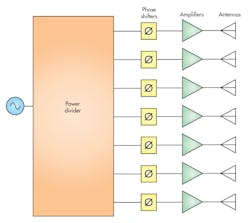
A phased-array antenna system can be defined as an array of antennas or radiating elements (Fig. 5). These elements could be located next to one another in a rectangular grid or even just in a line in the simplest case. The individual antenna beams constructively and destructively interfere with one another, depending on the phase of the signals being applied to the individual antenna elements. Thus, the antenna beams can combine to create a narrow beam in one specific direction, while cancellation occurs in the other directions. The direction of the beam can be varied by adjusting the phase of the signals being applied to the antenna elements.
5. Here’s a simplified block diagram of a phased-array antenna system.
A phased-array system can therefore change the direction of a beam without the need to physically move the antennas. Moreover, these systems can have hundreds or even thousands of individual antenna elements. Phased-array systems have several advantages in comparison to mechanical systems. For one, they are faster. In addition, phased-array systems eliminate the possibility of a mechanical failure.
Instruments for Radar Testing
Radar system testing can be accommodated by various test instruments for both signal generation and analysis. As radar systems have become more complex, the capabilities of modern test instrumentation have also advanced to meet these needs. Different types of instruments that can be used to generate and analyze radar signals include vector signal generators (VSGs), arbitrary waveform generators (AWGs), oscilloscopes, power meters, spectrum analyzers, and vector signal analyzers (VSAs).
Radar Signal Generation
Generating radar signals can be achieved by several different methods. VSGs are certainly one important instrument in terms of radar testing. They can generate modulated signals, such as the pulsed RF signals used in radar applications.
AWGs are also significant test instruments with regard to radar signal generation. A traditional approach for generating radar signals involves using an AWG to generate baseband signals, which are then applied to an RF modulator. This method results in a modulated signal that can be used in a radar test environment. However, newer AWGs are available that are capable of directly generating RF signals for radar testing.
Spectrum Analyzers and Vector Signal Analyzers
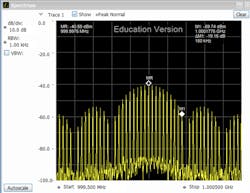
A spectrum analyzer can be used to analyze a pulsed RF signal in the frequency domain. Figure 6 is an illustration of a spectrum analyzer display of a pulsed RF signal. The spacing between the spectral components are determined by the PRF. The widths of the main lobe and side lobes are related to the pulse width. When using a spectrum analyzer to measure a pulsed RF signal, the resolution bandwidth (RBW) must be lower than the PRF in order to differentiate between each spectral component.
6. Such a display will typically be seen on a spectrum analyzer when measuring a pulsed RF signal.
VSAs offer measurement capabilities beyond that of a spectrum analyzer, as they can capture a signal’s magnitude and phase information. In addition to frequency-domain analysis, VSAs can display measurement results in the time and modulation domains. VSAs are highly effective for analyzing today’s more complex pulsed radar signals.
Power Meters
A power meter is another instrument that can be used to measure radar signals. An average power meter can measure the average power of a pulsed RF signal. The peak power can also be determined if the duty cycle is known. However, accurate measurements are possible only for an ideal pulse, as any pulse anomalies will result in inaccurate measurements. Thus, an average power meter may not be the best instrument to use to measure the peak power of a pulsed RF signal.
A peak power meter can be used to directly measure a pulsed RF signal’s peak power level. Peak power meters typically have trace display capabilities to allow one to see the envelope of a pulsed RF signal. An important parameter is video bandwidth, which must be sufficient to accurately track the envelope of a pulsed RF signal.
Oscilloscopes
Oscilloscope measurements date all the way back to early radar pulses. Some of today’s oscilloscopes offer measurement capabilities into millimeter-wave frequencies. Lastly, while VSAs and oscilloscopes both have many of the same measurement capabilities, tradeoffs also exist in terms of the measurements capabilities of each.