Algorithms to Antennas: Phased-Array Beam-Pattern Synthesis Using Deep-Learning Techniques
This blog is part of the Algorithms to Antennas Series
What you'll learn:
- Optimization of pattern-synthesis algorithms.
- Applying a deep-learning network to generate antenna element weights.
- Using a convolution neural network to perform pattern synthesis with deep learning.
We have discussed the use of optimization techniques to generate antenna element weights with a goal of generating a desired beam pattern without using a trial-and-error approach. Pattern synthesis is an important topic in array processing because array weights help shape the beam pattern of a sensor array to match a desired pattern.
This type of beam-pattern synthesis is used widely to direct energy to specific directions, to eliminate potential interference sources, or even to reduce the possibility of interfering with another system. For reference, check out our previous related posts: “Synthesizing an Antenna Array with Optimization Techniques” and “Optimization Techniques for Phased-Array Synthesis.”
Pattern-Synthesis Algorithms
Traditionally, pattern-synthesis algorithms leverage filter design techniques due to the similarity between spatial and frequency-domain signal processing. These algorithms often aren’t flexible enough to accommodate different kinds of constraints. Optimization techniques can provide a more general solution to produce desired patterns with more stringent requirements and constraint conditions.
While optimization-based algorithms are very flexible, for large arrays it can take a while to converge to the optimal solution. For fixed or pre-configured patterns, the extra computations aren’t an issue. However, for dynamic scenarios, this makes it more challenging to form a given beam pattern in real-time. Here, we will apply a deep-learning network to generate the antenna element weights. We will compare the results and execution time with the results we achieve using optimization techniques.
Deep-Learning Networks
Deep-learning networks need to be trained offline with many datasets, but once trained, the resulting networks can be used to achieve faster computation performance than optimization. Our example is inspired by a paper by Simone Bianco, et al., “AESA Adaptive Beamforming Using Deep Learning,” Proceedings of 2020 IEEE Radar Conference.
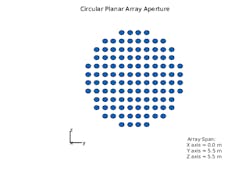
For the example, we use a circular planar array with a radius of 3 meters (Fig. 1). The antenna elements are located on a rectangular grid with an element spacing of 0.5 meters. Note the workflow we describe can be applied to other array geometries as well.
In this example, we would like to have a pattern whose mainlobe is along an azimuth and elevation of 0 degrees. Our pattern also should satisfy the following constraints:
- Maximize the directivity.
- Suppress interferences 50 dB below the mainlobe.
- Sidelobe levels between −20 and 20 degrees azimuth, or elevation must be below −17 dB.
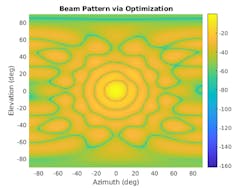
With all constraints defined, we can use an optimization solver to derive the array weights that provide us the desired pattern. Figure 2 shows an example of one beam pattern generated using optimization that meets the criteria described above.
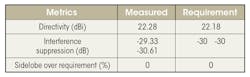
To verify the requirements are met, we can measure the quality of this pattern. The results are shown below:
We can see that the resulting metrics are very good. However, it does take some time to calculate the weights. On the machine that we ran this benchmark, it took about 22 seconds.
CNN Deep Learning
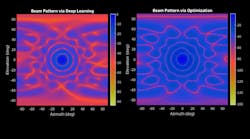
Now we perform pattern synthesis with deep learning using a convolution neural network (CNN). The beam patterns can be represented as images (Fig. 2, again). These images can be fed into the input layer to our regression network. The network outputs weights that when applied to the antenna array produces a beam pattern.
To train and test the network, we can generate patterns with random mainlobe and interference placements. The patterns and the ground truth weights generated using optimization are applied to train our network. The steps are shown in Figure 3.
As shown in Figure 4, we use test patterns that the network hasn’t seen before as the input to compute the antenna element weights at the output of the network. Those weights are applied to the corresponding elements to generate a pattern.
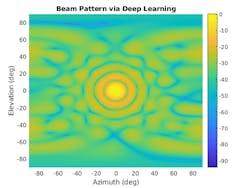
Figure 5 illustrates an example of the pattern generated using a trained network.
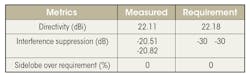
We can measure the results qualitatively as indicated below:
We can see that the predicted pattern provides good results in terms of directivity and sidelobe suppression. It’s not as good as achieving the interference suppression as the optimization technique provided. This can be improved by using more training data.
The other result is that when using the same processor to generate the weights, it took about 7 seconds, which is significantly less time than the optimization result. In addition, with a GPU device, the processing time can be significantly accelerated beyond the time it takes on a processor.
Although the deep-learning network can generate pattern-synthesis weights much faster, the network requires a large amount of data to train. In addition, the network is specific to a specific array geometry. Therefore, if the array formation changes, the network must be retrained.
To learn more about the topics covered in this blog and explore your own designs, see the examples below or email me at [email protected]:
- Array Pattern Synthesis using Nulling, Windowing, and Thinning (Example): Learn how to taper element responses so that the resulting array pattern satisfies certain performance criteria.
- Array Pattern Synthesis using Optimization Techniques (Example): Learn how to use optimization techniques to perform pattern synthesis.
- Phased Array Modeling (Documentation): Learn to perform phased design and analysis.
See additional 5G, radar, and EW resources, including those referenced in previous blog posts.
Rick Gentile is Product Manager, Honglei Chen is Principal Engineer, and Alex Wu is a Software Engineer at MathWorks.