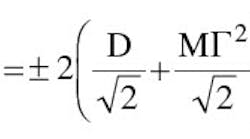Portable vector network analyzers (VNAs) have brought new mobility to one of the most trusted instruments in the RF/microwave industry. The new model LA19-13-02 portable analyzer from LA Techniques (www.latechniques.com), for example, features a compact footprint but full S-parameter measurement capability from 3 MHz to 3 GHz. Of course, a major consideration before acquiring a portable VNA is its accuracy and reliability.
Recently, a collaboration between LA Techniques and the United Kingdom's national measurement standards laboratory, the National Physical Laboratory (NPL), focused on establishing reliable accuracy metrics for this low-cost portable VNA (Fig. 1). This work built on other recent work where new calibration methods were developed to enable this type of VNA to achieve unprecedented levels of accuracy using budget priced calibration kits.1,2
In order to understand this assessment of portable VNA accuracy and reliability, it may be useful to examine the portable VNA's system architecture, and then review the methods used to characterize the calibration standards, including the concept of load "breeding." In load breeding, a parent load can be used to produce offspring loads with characterized performance so that the offspring loads can also be used as reliable VNA calibration standards. Following an evaluation of these loads, this article will review the achievable accuracy for this type of VNA and shows some measurement comparisons with the UK's national standard facilities to demonstrate the accuracy statements.
Figure 2 shows a schematic diagram of the LA19-13-02 VNA system. The unit operates under the control of an external personal computer (PC). The VNA's internal controller is tasked with setting the hardware operation and carrying out partial averaging of the measured data in order to minimize the traffic through the serial interface.
The VNA employs a tuned receiver with mixer-based frequency down-converters and synchronous detectors. A noise-cancellation technique allows very low trace noise to be achieved with a simple hardware implementation. The unit includes two frequency synthesizers, one to generate the test signal (at levels from 20 to 0 dBm) and another to generate the local-oscillator (LO) signals for the receiver. The synthesizers are based on direct-digital-synthesis (DDS) technology and achieve a worst-case settling time of 290 s to within 1 kHz of a new frequency with a worst-case phase noise of 71 dBc/Hz offset 22 kHz from the carrier.
Because of space constraints, directional bridges (C1 and C2 in Fig. 2) are used to extract reflection and transmission signals. Bridges are typically more compact than other types of directional couplers (e.g., stripline edge couplers) for very wideband applications albeit with a higher insertion loss. Included in the VNA are wideband bias Ts to allow as much as 250 mA DC bias injection when testing active devices such as transistors and amplifiers.
The user-interface (UI) software runs on the external PC and carries out virtually all of the data processing. It includes numerous features such as real time de-embedding, automatic and manual reference plane extension, importing and displaying of data files for live comparisons with measurement data, vector mathematics on memory traces, and numerous marker functions such as peak and minimum search and 3-dB-bandwidth calculations.
Control of the instrument from other programs such as LabView from National Instruments (www.ni.com) and VEE from Agilent Technologies (www.agilent.com) is possible using the dynamic-link-library (DLL) code supplied with the instrument. The library supports high-level commands to simplify the control of the VNA in automatic-test-equipment (ATE) systems, making control of the VNA in automated test systems easy.
The LA19-13-02 VNA is calibrated using the short-open-load-through (SOLT) technique. The calibration kits (Fig. 3) supplied with the VNA contain budget-priced components so that the overall cost of the VNA package is kept to a minimum. However, the performance of these budget-priced components is greatly enhanced by applying accurate characterization routines using the VNA's firmware. This results in state-of-the-art VNA performance, i.e., as good as can be achieved using high-precision calibration standards and/or more sophisticated calibration routines.
In conventional calibration schemes, the VNA standards are often assumed to have ideal characteristics. For example, short- and open-circuit standards are assumed to have a magnitude voltage reflection coefficient (VRC) equal to unity. Similarly, the load standard is assumed to have a VRC of zero, i.e., it is assumed to be a perfect match. For short-circuit/open-circuit standards, such assumptions are reasonable for most applications. However, the assumption that the load standard is a perfect match can never truly be met. This is particularly relevant when the load is not a high-precision component (as is the case here) and this causes significant residual errors to remain in the VNA after a conventional calibration.
The approach to calibration used by the LA19-13-02 VNA acknowledges that the load standard does not provide a perfect match and uses measurement data to 'characterize' the load so that its nonzero VRC can be taken into account and used during the calibration process. This method continues to work well even when the calibration load produces significant amounts of reflectiona condition that is usually associated with poor calibration performance. The technique, therefore, is particularly useful when low-cost components are used as the standards. Under these conditions, the only requirement is that the measured value of the standard is repeatable, and this is achieved using a precision connector at the device interface.
The characterization of the load standard involves obtaining reliable measurements of the load at DC and RF. Specifically, the resistance is measured at DC and the complex VRC is measured at RF. Only modest accuracy is required for the DC measurement, e.g., to within a few milliohms, and this can be achieved using an off-the-shelf calibrated digital ohmmeter. Greater accuracy is required for the complex VRC measurements, and these are made over a range of frequencies that corresponds to the VNA's bandwidth, i.e., 3 MHz to 3 GHz. These RF measurements were originally supplied to the VNA manufacturer (LA Techniques) by NPL using the UK's primary national standard measurement system.
Page Title
Two polynomials are then fitted to the (complex-valued) measurement dataone to the real part and one to the imaginary part of the datausing simple fitting routines. Each fit includes a value at DC: either the measured resistance for the fit to the real part of the data; or, zero for the fit to the imaginary part of the data (i.e., the reactance at DC). The coefficients of the polynomial are then stored so that values of complex VRC can be subsequently generated at any required frequency and used by the VNA during the calibration process. This ensures that a close approximation to the actual complex VRC of the load is used at each frequency during calibration.
The characterization of the open-circuit and short-circuit standards is more straightforward since these standards more closely approximate to the ideal condition. For the open circuits, the VRC phase is characterized using capacitance polynomials optimised to the bandwidth of the VNA.3 For the flush short circuits, no additional characterization is needed at these frequencies.
Having obtained a characterized load standard from one of the LA Techniques calibration kits, it is straightforward to produce additional characterized loads using this initial parent' load and the VNA as the transfer instrument. The VNA firmware contains the necessary features to both characterize a load and then subsequently use it as a calibration standard. The process of breeding characterized loads in this way can be performed either at the LA Techniques manufacturing facility or directly by the end user.
The method used to evaluate the accuracy of the VNA follows recommended practices.4 However, the overall uncertainty given here does not include contributions from random errors, e.g., connector repeatability, system repeatability, cable flexure, noise, and ambient conditions. This is because, except for noise, these random errors are external to the VNA and so are not representative of the performance of the VNA itself. Instead, these errors are caused by other components in the overall measurement processi.e., the cables and adaptors used to form the measurement reference planes, the devices connected to the reference planes (both calibration standards and the devices that are subsequently measured by the VNA)and the environment in which the VNA is operated. The overall uncertainty therefore represents a Best Measurement Capability5 that can be used for defining a Scope of Accreditation6 for measurements made using this type of VNA and calibration kit (e.g., by an accredited calibration or test house). However, since worst-case estimates are used to represent the errors this is likely to lead to a conservative estimate of the overall uncertainty for the VNA when used under everyday operating conditions.
The most significant systematic errors that affect the accuracy of the VNA are:
- Residual directivity, D
- Residual test port match, M
- Residual load match, *L
- Detector nonlinearity, L
- Test-set cross-talk/isolation, dA
- Test port mismatch, MTM
These are errors that remain after calibration and so become sources of uncertainty for all subsequent measurements made by the VNA. For consistency, the choice of symbols used for these error terms follows that given in ref. 4.
A full description of the evaluation of each of these errors is given in ref. 7, from which a summary is presented here. For example, the residual directivity of each of the VNA's measurement reference planes is assessed by attaching a long beadless airline terminated with a well-matched load. Examples of the resulting ripple traces are shown in Fig. 4, in terms of linear VRC. The residual directivity is given by one-half the difference between adjacent maxima and minima of the ripple trace. Therefore, the worst-case value for the residual directivity VRC is approximately 0.004.
In a similar way, the residual test port match can be found by attaching the same airline, except terminated with a high reflection (e.g., a short circuit). This results in a worst-case residual test port match VRC of typically 0.010. The residual load match is related to the uncertainty in measuring the VNA's uncorrected load match. For this VNA, the uncorrected load match VRC has been measured as being generally less than 0.07 and so the worst-case residual load match VRC is 0.006. (This value has been determined using Eq. 1, where the measured VRC is the uncorrected load match and the uncertainty in measured VRC is the residual load match error.)
The nonlinearity of the detectors is determined by measuring a calibrated step attenuator over a 50-dB dynamic range. This is done at several different frequencies across the VNA's bandwidth. The difference between the VNA readings and the calibrated values for the step attenuator enables a worst-case error due to nonlinearity to be determined. For this VNA, this error was generally found to be not more than 0.002 dB/dB. The test set isolation can be determined by measuring the amount of transmitted signal when both VNA test ports are terminated. For this VNA, the worst-case observed isolation across the full bandwidth was found to be 83 dB.
The uncertainty due to test port mismatch is very much dependent on the S-parameters of the devices being measured. Therefore, to keep things simple, only relatively well-matched devices are considered here (e.g., with magnitude VRC Tables 1 and 2.
For a one-port device, the uncertainty, U(*), of a VRC measurement is determined using:
where:
* = the measured magnitude VRC of the device under test (DUT).
Page Title
Values of D and M given in Table 1 are used to calculate U(*) from which the equivalent return-loss uncertainty is obtained using equations in ref. 8. (For convenience, these equations are reproduced in the sidebar, "Calculating return-loss uncertainty.") A plot of Return-Loss Uncertainty versus measured return loss is shown in Fig. 5a. Similarly, the associated uncertainty in reflection phase is shown in Fig. 5b. The phase uncertainty has been calculated using equations obtained from ref. 9. (These are also reproduced in the sidebar.)
In general, the uncertainty for reflection measurements of two-port devices will be similar to that for one-port devices. A significant difference will only occur when measuring low values of attenuation (i.e., less than 6 dB), when effects due to the residual load match of the VNA receiver port become significant. Therefore, as a rule of thumb, Figs. 5a and 5b can be used for two-port devices when the measured attenuation is greater than 6 dB. When the attenuation is less than 6 dB, modified plots (that have been given in ref. 7), that take into account the residual load match contribution, should be used.
The uncertainty, U, for attenuation measurements of two-port devices is determined using:
The values of L, MTM , and dA in Table 2 are used to calculate the uncertainty in attenuation and transmission phase (using Eqs. 4 and 5). These are shown in Figs. 6a and 6b.
It is interesting to deconstruct' the overall attenuation uncertainty Fig. 6a> into its constituent partsnamely, the nonlinearity, mismatch, and isolation/crosstalk terms. This deconstruction is presented in Fig. 7, which shows the sizes of each of these terms along with the resulting overall combined uncertainty, expressed at the "one standard deviation" (or "one sigma") level. This plot shows that for low levels of measured attenuation (i.e., to 10 dB), mismatch is the dominant uncertainty; for intermediate levels (10 dB to approximately 35 dB), nonlinearity is the dominant uncertainty; and, for high levels (35 dB and above), isolation/crosstalk is the dominant uncertainty.
Some intercomparisons of measurements have been made between the LA19-13-02 VNA and the UK national standard facilities at NPL and these are presented here as graphs. Each set of results also shows the uncertainties for the LA19-13-02 VNA measurements using values shown in Figs. 5 and 6. These uncertainties are, in general, not much larger than the uncertainties for the reference values supplied by NPL. Results for two devices are presented: a mismatched termination with nominal VSWR of 2.0:1 and a 20-dB attenuator. The measured phases for these devices vary rapidly with frequency. Therefore, to present these results in a more useful way, a plot of the difference between the LA19-13-02 and NPL values is given. This effectively normalizes the results to the values given by NPL.
The mismatch with nominal VSWR of 2.0:1 has an equivalent magnitude VRC of 0.333 and an equivalent return loss of 9.54 dB. Using Eqs. 1 and 3, the uncertainty in magnitude VRC is 0.007 3 and the equivalent return loss uncertainty is 0.19 dB. This value of uncertainty is shown as error bars applied to the results in Fig. 8a, which also shows the results obtained by NPL.
Using Eq. 4, the uncertainty in reflection phase is 1.3 deg. This value of uncertainty is shown as error bars in Fig. 8b, which shows the differences between the LA19-13-02 and the NPL measured values.
For the 20-dB attenuator, the uncertainty in the measured attenuation, calculated using Eq. 2, is 0.046 dB. This value of uncertainty is shown as error bars applied to the results in Fig. 9a along with the results obtained by NPL. The uncertainty in transmission phase, calculated using Eqs. 4 and 5, is 0.31 deg. This value of uncertainty is used in Fig. 9b, which shows the differences between the LA19-13-02 and NPL measured values.
This article has given a performance review of the latest model of VNA available from LA Techniques. In particular, it has shown that by using characterized calibration standards very good measurement accuracy is obtained without the need to use precision components. This is achieved by using measurement-derived data during the calibration of the VNA. Measurement intercomparisons between the LA19-13-02 VNA and NPL have shown very good agreement (i.e., the uncertainties for the LA19-13-02 measurements encompass the values obtained by NPL). This shows that the uncertainties established for the LA19-13-02 are realistic.
The overall uncertainty in reflection measurements varies depending on the size of the measured reflection. This is summarized in Table 3, which gives values at the extremes of the measurement range, i.e., at magnitude VRC equal to zero and one.
The overall uncertainty in attenuation measurements also varies with the size of the measured attenuation. This is summarized in Table 4 for selected values of attenuation to 60 dB. Beyond 60 dB, the error due to isolation/crosstalk in the VNA dominates the overall measurement uncertainty.
Page Title
The summary of VNA measurement uncertainties presented here provides a performance specification for the accuracy of the LA19-13-02 VNA that has been independently verified by a national measurement standards laboratory (NPL). It is considered that the demonstrated accuracy compares favorably with VNAs made by the other leading manufacturers of these instruments.
Acknowledgment
The work described here was partially funded by the UK government. Specifically, the Measurement for Innovators Programme of the National Measurement System Directorate, Department of Trade and Industry. © Crown Copyright 2007. Reproduced by permission of the Controller of HMSO.
References
- Nick Ridler and Nils Nazoa, “Using simple calibration load models to improve accuracy of vector network analyzer measurements,” 67th ARFTG Conference Digest, pp. 104-110, San Francisco, CA, June 2006.
- Nils Nazoa and Nick Ridler, “LA19-13-01 3 GHz VNA calibration and measurement uncertainty,” LA Techniques Ltd, Technical Note Ref LAP02, January 2006. Available from www.latechniques.com.
- M.J. Salter and N.M. Ridler, “Measuring the capacitance coefficients of coaxial open-circuits with traceability to national standards,” Microwave Journal, Vol. 49, No. 10, October 2006, pp. 138-154.
- “EA guidelines on the evaluation of Vector Network Analysers (VNA),” European co-operation for Accreditation, publication reference EA-10/12, May 2000.
- “Expression of the uncertainty of measurement in calibration,” European co-operation for Accreditation, publication reference EA-4/02, December 1999.
- ISO/IEC 17025: 2005, “General requirements for the competence of testing and calibration laboratories.”
- Nils Nazoa and Nick Ridler, “LA19-13-02 3 GHz VNA calibration and measurement uncertainty,” LA Techniques Ltd, Technical Note Ref LAP03 (to be published). Available from www.latechniques.com.
- N.M. Ridler, “Converting between logarithmic and linear formats for reflection and transmission coefficients,” ANAMET Technical Note, No. 4, October 2000. Available from www.npl.co.uk/anamet.
- N.M. Ridler and J.C. Medley, “An uncertainty budget for VHF and UHF reflectometers,” NPL Report DES 120, May 1992. Available from www.npl.co.uk.