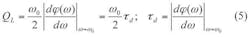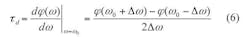Approach Drops SMD DRO Phase Noise
Download this article in .PDF format
This file type includes high resolution graphics and schematics when applicable.
Phase noise is an oscillator parameter that grows in importance with the complexity of modern communications modulation formats. Fortunately, work on dielectric resonator oscillators (DROs) at Synergy Microwave Corp. has resulted in a line of compact surface-mount-device (SMD) DROs with extremely low phase-noise levels at fundamental-frequency outputs through 6 GHz and higher, suitable for use in commercial, industrial, and military applications.
Related Articles
• Searching For Low-Phase-Noise Synthesizers
• Gallium Nitride Drives Power Amplifier Performance
• Generating Reliable RF/Microwave Signals
A Mobius coupling mechanism is employed to help miniaturize the planar dielectric resonators in these oscillators. The design approach helps maintain small size for these oscillators even at lower frequencies, with the low phase noise and low thermal drift required for a wide range of military, industrial, medical, and test-and-measurement applications.
These new DROs rely on planar resonators based on metamaterial Möbius strips (MMS), which are simple examples of anholonomy. The geometrical phenomenon of anholonomy depends on the failure of a quantity to recover its original value, when the parameters on which it depends are varied around a closed circuit.1-3 Metamaterials are engineered periodic composites that have negative refractive-index characteristics not available in natural materials.4-7 Such materials, in typically arrangements with split rings (SRs) and metallic conducting wires, can achieve values of negative permeability (-μ) and negative permittivity (-ε).8
In general, the refractive index of a medium can be characterized by four possible sign combinations for the permeability-permittivity pair (με) and can be described9-18 by means of Eqs. 1-4:
n = [(+ε)(+μ)]0.5 = (+)(με)0.5 (1)
n = [(-ε)(+μ)]0.5 = j(με)0.5 (2)
n = [(-ε)(-μ)]0.5 = (-)(με)0.5 (3)
n = [(+ε)(-μ)]0.5 = j(με)0.5 (4)
where:
ε0 = 8.85 × 10-12 F/m,
μ0 = 4π × 10-7 H/m, and
n = the refractive index of the medium.
Equation 1 is valid for double positive substrate (DPS) materials, with permittivity and permeability both positive; Eq. 2 is valid for ε negative (ENG) substrate materials, with negative permittivity and positive permeability; Eq. 3 is for double negative (DNG) substrate materials, with permittivity and permeability both having negative values; and Eq. 4 is for μ negative (MNG) substrate materials, where the permeability is negative but the permittivity has positive values.
The DNG materials described by Eq. 3 are typically defined as artificial materials and commonly referred to as “metamaterials” in the technical literature. They are alternately known as left-handed materials (LHMs), negative index materials (NIMs), and backward-wave materials (BWMs).19 The unusual characteristics of metamaterials, such as backward-wave propagation, exhibit group velocity characteristics in a direction opposite to that of its phase velocity, causing strong localization and enhancement of fields. This can result in significant enhancement of a resonator’s quality factor (Q), assuming losses can be minimized.20
The realization of true DNG material (metamaterial) is questionable. In general, it is difficult to build a material or medium simultaneous with negative permittivity and negative permeability for broad operating frequency ranges from a set of arbitrary passive structure unit cells arranged in predetermined order. This may lead to a violation of energy conservation principle at the intersecting plane between a right-handed material (RHM) and LHM media because of the generation of energy.
An attempt to build the DNG material or medium—based on the fact that for a specific orientation and arrangement of the passive structure, the values of permittivity and permeability diminish as the frequency increases—has been applied to demonstrate virtual negative permittivity and permeability at specific frequencies, but it lacks validity for broadband operation. In reality, it is easier to demonstrate independently negative permeability or negative permittivity, but achieving both negative characteristics in a DNG material can be difficult.
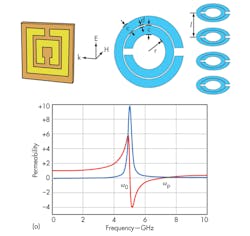
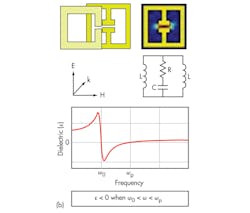
Printed multicoupled slow-wave resonators exhibit improved Q-factor characteristics, and are commonly employed in low-phase-noise oscillator applications.21 For example, improvement in the Q-factor of a slow-wave resonator (λ/4 coplanar stripline) can be realized by forming an open-circuit load where the incident and reflected electromagnetic (EM) waves move entirely in-phase with each other. In reality, such open-circuit conditions are difficult to maintain over a desired frequency band. In addition, the implementation of a λ/4 coplanar stripline circuit on a substrate can increase the overall size of the circuit. Insertion of additional floating metal shields may help alleviate some of the problems with slow-wave circuit designs.21-25 But negative-permeability-based planar split-ring-resonator (SRR) structures and complementary split-ring-resonator (CSRR) structures can enable compact on-chip implementations of these circuits, with promising and cost-effective solutions for metamaterial oscillator and filter applications.26-29
In the proper arrangement, planar SRR and CSRR structures can achieve independently negative permeability and negative permittivity at the resonance needed to create optimum coupling for a disc resonator in a high-performance DRO. These structures can be characterized as magnetic and electric dipoles excited by the magnetic (H) and electric (E) fields along the ring axis.7
Interestingly, a single-negative property (-ε or -μ) supported by an SRR or CSRR structure can yield a sharp stopband in the vicinity of the resonant frequency. This enables storage of EM energy into an SRR or CSRR structure through an evanescent-mode coupling mechanism, resulting in high Q. It should be noted that the Q multiplier effect does not violate the law of conservation of energy since the evanescent mode in an SRR stores energy but does not transport energy.21
A Closer Look
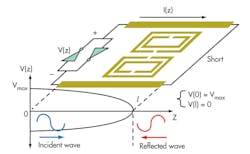
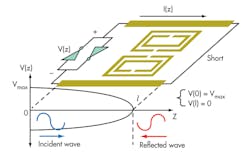
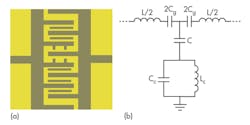
Figure 1 shows a typical differential transmission-line-loaded, SRR-based metamaterial resonator oscillator. For a differential (push-pull) oscillator, the incident wave energy injected by the cross-coupled inverters propagates in forward waves along the transmission line towards the circuit’s short point; the energy is reflected at the SRR load, and the reverse wave has a superposition of the incident wave and leads to a resonance when in phase. Stronger wave reflection means less loss and higher resonator Q.20
Möbius strips offer unique characteristics, including self-phase-injection properties along the mutually coupled surface of the strips, enabling enhanced Q for a given size of printed transmission-line resonator. The oscillator’s loaded Q, QL, is described by Eqs. 5 and 6:
where:
φ(ω) = the phase of the oscillator’s open-loop transfer function at steady state and
τd = the group delay of the metamaterial Möbius strip resonator.
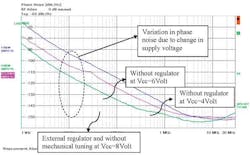
These oscillators should be powered by a clean DC bias voltage, otherwise an external regulator should be employed to minimize variations in supply voltage. A DRO factory set for an output frequency of 10 GHz, for example, can be mechanically adjusted by about ±50 MHz.
An electrical tuning port provides an adjustment range of ±1 MHz with tuning voltages of +1 to +15 VDC to compensate for frequency drift in phase-locked systems. The supply-current is typically 30 mA and the temperature range is specified from -25 to +70°C.
Dr. Ajay K. Poddar, Chief Scientist
Dr. Ulrich L. Rohde, Chairman
Synergy Microwave Corp., 201 McLean Blvd., Paterson, NJ 07504; (973) 881-8000, FAX: (973) 881-8361
Editor's Note: Ulrich L. Rohde was recently named the recipient of the 2014 C.B. Sawyer Award.
References
1. A.K. Poddar, U.L. Rohde, and D. Sundarrajan, “Real Time Signal Retention Device using Co-planar Waveguide (CPW) as Mobius strip,” 2013 IEEE MTT-S Digest, June 2013, pp. 1-3.
2. A.K. Poddar, U.L. Rohde, and D. Sundarrajan, “A Novel Mobius-Coupled Printed Resonator Based Signal Sources,” 2013 IEEE MTT-S Digest, June 2013, pp. 1-3.
3. U.L. Rohde and A.K. Poddar, “A Novel Evanescent-Mode Mobius-Coupled Resonator Oscillators,” IEEE Joint UFFC Symposia with European Frequency and Time Forum (EFTF) and Piezo response Force Microscopy, July 21-25, 2013.
4. V. Veselago, “The electrodynamics of substances with simultaneously negative values of ε and μ,” Soviet Physics-Solid State, Vol. 8, No. 12, 1967, pp. 2854-2856.
Related Articles
• Searching For Low-Phase-Noise Synthesizers
• Gallium Nitride Drives Power Amplifier Performance
• Generating Reliable RF/Microwave Signals
5. V.G. Veselago, “The electrodynamics of substance with simultaneously negative values of ε and μ,” Soviet Physics Uspeki, Vol. 10, 1968, pp. 509-514.
6. J.B. Pendry, A.J. Holden, D.J. Robbins, and W.J. Stewart, “Magnetism from conductors and enhanced nonlinear phenomena,” IEEE Transactions on Microwave Theory & Techniques, Vol. 47, 1999, pp. 2075-2084.
7. R.A. Shelby, D.R. Smith, and S. Schultz, “Experimental verification of a negative index of refraction,” Science Vol. 292, 2001, pp. 77-79.
8. J. Manuel and T. Alves, “Metamaterials with Negative Permeability and Permittivity: Analysis and Application,” M. S. thesis, University Tecnica de Lisboa Instituto Superior Tecnico, 2010.
9. U.L. Rohde, A.K. Poddar, T. Itoh, and A. Daryoush, “Evanescent-Mode Metamaterial Resonator Based Signal Sources,” IEEE IMaRC Delhi, December 14-16, 2013.
10. U.L. Rohde, A.K. Poddar, T. Itoh, and A. Daryoush, “Evanescent-Mode Metamaterial Resonator Based Signal Sources,” IEEE IMaRC Delhi, December 14-16, 2013.
11. A.K. Poddar, U.L. Rohde, and T. Itoh, “Metamaterial Mobius Strips (MMS): Tunable Oscillator Circuits,” Proceedings of the 2014 International Microwave Symposium, Tampa, FL, June 2014.
12. C.-T. M. Wu, A.K. Poddar, U.L. Rohde, and T. Itoh, “A C-band Tunable Oscillator Based on Complementary Coupled Resonator using Substrate Integrated Waveguide Cavity,” submitted to European Microwave Symposium 2014.
13. M. Martin, et al., “Miniaturized coplanar waveguide stop band filters based on multiple tuned split ring resonators,” IEEE Microwave & Wireless Component Letters, Vol. 13, 2003, pp. 511-513.
14. Joan, et al., “Microwave filters with improved stopband based on sub wavelength resonators,” IEEE Transactions on Microwave Theory & Techniques, Vol. 53, 2005, pp. 1997-2006.
15. Bonache, et al., “Novel microstrip bandpass filters based on complementary split-ring resonators. IEEE Transactions on Microwave Theory & Techniques, Vol. 54, 2005, pp. 265-271.
16. J.B. Pendry, A.J. Holden, D.J. Robbins, and W.J. Stewart, “Magnetism from conductors and enhanced nonlinear phenomena,” IEEE Transactions on Microwave Theory & Techniques, Vol. 47, 1999, pp. 2075-2084.
17. J.B. Pendry, “Negative Refraction Makes a Perfect Lens,” Physical Review Letters, Vol. 85, No. 18, October 2000.
18. J.B. Pendry, A.J. Holden, D.J. Robbins, and W. J. Stewart, “Low frequency plasmons in thin-wire structures,” Journal of Physics: Condensed Matter, Vol. 10, No. 22, June 1998, pp. 4785-4809.
19. W. Fei Shang, et al., “96-GHz oscillators by High Q-Differential Transmission Line Loaded with Complementary Split-Ring Resonator in 65-nm CMOS,” IEEE Transactions on Circuits and Systems-II, Express Briefs, Vol. 60, No. 3, March 2013, pp. 127-131.
20. Y. Shang, et al., “Design of High-Q Millimeter-Wave Oscillator by Differential Transmission Line Loaded with Metamaterial Resonator in 65-nm CMOS,” IEEE Transactions on Microwave Theory & Techniques, Vol. 61, No. 5, May 2013, pp. 1892-1902.
21. A.K. Poddar, “Slow Wave Resonator Based Tunable Multi-Band Multi-Mode Injection-Locked Oscillators,” Dr.-Inh.-habil thesis, BTU Cottbus, Germany (draft thesis submitted for defense on March 2013).
22. D. Huang, W. Hant, N.-Y. Wang, T. Ku, Q. Gu, R. Wong, and M.-C. Chang, “A 60 GHz CMOS VCO using on-chip resonator with embedded artificial dielectric for size, loss and noise reduction,” in IEEE International Solid-State Circuits Conference, February 2006, pp. 1218-1227.
23. D. Kim, J. Kim, J.-O. Plouchart, C. Cho, D. Lim, W. Li, and R. Trzcinski, “A 75 GHz PLL front-end integration in 65 nm SOI CMOS technology,” in IEEE VLSI Circuits Symposium, June 2007, pp. 174-175.
24. G. Liu, R. Berenguer, and Y. Xu, “A mm-wave configurable VCO using MCPW-based tunable inductor in 65-nm CMOS,” IEEE Transactions on Circuits & Systems II, Experimental Briefs, Vol. 58, No. 12, December 2011, pp. 842–846.
25. O. Momeni and E. Afshari, “High power terahertz and millimeter-wave oscillator design: A systematic approach,” IEEE Journal of Solid-State Circuits, Vol. 46, No. 3, March 2011, pp. 583-597.
26. R. Liu, A. Degiron, J.J. Mock, and D.R. Smith, “Negative index material composed of electric and magnetic resonators,” Applied Physics Letters, Vol. 90, No. 26, June 2007, pp. 263504 1-263504 3.
27. R.A. Shelby, D.R. Smith, and S. Schultz, “Experimental verification of a negative index of refraction,” Science, Vol. 292, No. 5514, 2001, pp. 77-79.
28. C.-J. Lee, K. Leong, and T. Itoh, “Composite right/left-handed transmission line based compact resonant antennas for RF module integration,” IEEE Transactions on Antennas & Propagation, Vol. 54, No. 8, August 2006, pp. 2283-2291.
29. F. Falcone, T. Lopetegi, J. Baena, R. Marques, F. Martin, and M. Sorolla, “Effective negative-epsiv-stopband microstrip lines based on complementary split ring resonators,” IEEE Microwave & Wireless Component Letters, Vol. 14, No. 6, June 2004, pp. 280-282.
This file type includes high resolution graphics and schematics when applicable.
About the Author
Ulrich L. Rohde
Chairman of Synergy Microwave Corp
Ulrich L. Rohde is Chairman of Synergy Microwave Corp., Paterson, NJ and President of Communications Consulting Corp. Rohde studied electrical engineering and radio communications at the universities of Munich and Darmstadt, Germany. He holds a PhD in electrical engineering (1978) and an Sc.D. (hon., 1979) in radio communications. In 2004, he obtained a Dr.-Ing. Degree from the University in Berlin, Germany. In 2011, Rohde earned the Prof. Dr.-Ing. habil. degree from the University of Cottbus, Germany. Rohde has published more than 200 scientific papers and either contributed to or written a large number of books.