Manage Quartz Crystals Under High Vibration
This file type includes high resolution graphics and schematics when applicable.
Crystal oscillators have long been frequency sources with excellent frequency stability, spectral purity, and low phase noise. Unfortunately, a crystal oscillator’s noise performance can be affected by vibration or other acceleration events in the application environment. Even moderate levels of vibration can significantly affect a low-noise signal. Understanding the behavior of a crystal oscillator under various conditions of vibration and acceleration can help improve the overall performance of an application that must operate under those conditions.
Related Articles
• Connector Couples High-Speed Signals
• Oscillators Are Steady With Temperature
• Microwave Diodes… Why a Schottky-barrier? Why a Point-contact?
For a crystal oscillator operating within different mobile platforms, vibration-induced phase noise can be greater than all other noise sources combined.1 For many electronic systems, operation in the presence of vibration became an important requirement, as the sensitivity of different components to vibration and acceleration was found to be degrading system performance. Although many components contributed to the problem, in many cases quartz crystal resonators and oscillators were found to be limiting the overall noise performance of these electronic systems.
As a result, it was necessary to improve the dynamic characteristics of quartz crystals and oscillators, as well as to expand the theoretical understanding of quartz and its applications.2-4 Some improvements in quartz crystals have developed in the ensuing years, but the intrinsic acceleration sensitivity characteristic of most crystal resonators is still very similar to its state of more than 40 years ago.5
The acceleration sensitivity (also referred to as the “g-sensitivity”) of a well-designed crystal oscillator is primarily a function of the crystal resonator. All quartz crystals have an intrinsic characteristic that causes a small change in resonant frequency when subject to a change in acceleration. This is primarily due to the strain that is applied to the resonator through the mounting and support structure which causes deformation of the quartz.6
Empirical evaluation has shown that the acceleration sensitivity of quartz is vectorial in nature: dependent upon the direction of the applied force. Therefore, the resultant effect of acceleration on the frequency of a given crystal is determined by the instantaneous magnitude of the acceleration as well as the direction in which it is applied. The frequency shift is a maximum when applied in a direction parallel to the force vector.
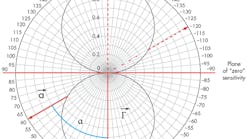
As shown in Fig. 1, as the angle between the force vector and the acceleration sensitivity vector increases from 0 deg. to 90 deg., the effective sensitivity rolls off as the cosine of the angle, approaching 0 at an angle of 90 deg. Therefore, any force that is applied in the plane normal to the vector will have a minimal effect on the crystal. This is depicted in two dimensions by the circles in Fig. 1. The bottom circle depicts the positive frequency shift that occurs when the force is applied in the same direction as the Γ vector. (The acceleration sensitivity of a crystal or oscillator is typically denoted by Γ.)
The top circle represents the negative frequency shift of equal magnitude produced when the same force is applied from the opposite direction. This is the case when sinusoidal vibration is applied. As the direction of the acceleration force is constantly shifting 180 deg. at the frequency of vibration, the resonant frequency of the crystal is shifting positively and negatively about the nominal center frequency, effectively applying frequency modulation (FM) to the crystal resonator’s output signal.
When viewed in three dimensions, the Γ circles are rotated about the Γ axis to form spheres, as shown in Fig. 1a. This model can then be inserted into the oscillator’s frame of reference with the model’s Γ vector aligned parallel to the actual Γ vector of the oscillator. It is then possible to predict the effective Γ for acceleration force that is applied in any direction.
The frequency during acceleration can then be written in Eq. 1 as the product of two vectors,
f(a) = f0(1 + Γ·a) (1)
where:
f0 = the carrier frequency with no acceleration;
Γ = the acceleration sensitivity vector; and
a = the acceleration force vector.
The magnitude of Γ is usually linear versus the applied force to greater than 50 g’s.4 The frequency response of Γ is also relatively flat. Nonetheless, vibration frequencies of several kHz through mechanical resonances in the blank and mounting structures may cause peaking in some areas, depending upon the type of crystal.
This file type includes high resolution graphics and schematics when applicable.
Characterizing A Source
This file type includes high resolution graphics and schematics when applicable.
The acceleration sensitivity of an oscillator that will be used in a high-vibration environment would typically be characterized by applying a known vibration level (time-dependent acceleration) to the oscillator and then observing the effect of the vibration on its output spectrum. When the applied vibration is a single-frequency sine wave, a discrete spurious product will be produced offset from the carrier by the vibration frequency. By measuring the level of this spurious signal relative to the power of the carrier, the amount of frequency deviation may be determined from FM theory. Normalizing by the magnitude of the vibration will then give the amount of frequency shift per g of acceleration in the axis of vibration. This is the definition of acceleration sensitivity or Γ. For a crystal oscillator where the fractional frequency shift is very small, Γ is usually expressed in parts per billion per g (1 ppb/g = 1 × 10-9/g). The level of the sideband that will be produced when the excitation is a single-frequency sine wave is closely approximated by Eq. 2:
SB level (dBc) = 20log[(a × Γ × fnom)/2fv] (2)
or, solving for Γ gives:
Γ = (2fv/a × fnom × 10dBc/20 (3)
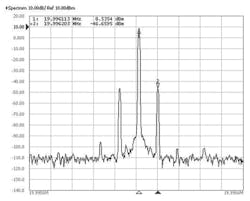
where a is the peak magnitude of the vibration force in the direction of Γ being measured, fv is the frequency of the sine wave vibration, and fnom is the nominal carrier frequency at rest. Figure 2 shows the spectrum of a 20-MHz crystal being vibrated with a peak acceleration of 10 g’s at 90 Hz. As can be seen from the difference between the two markers, the vibration-induced sideband is 55.2 dB below the carrier. According to Eq. 3, the magnitude of Γ of this crystal in the axis being vibrated is therefore 1.56 ppb/g.
To determine the exact magnitude and the directional orientation of the vector, it is necessary to measure the response along three mutually perpendicular axes, usually selected to be normal to the faces of the oscillator package for use of alignment. But the Γ vector is typically not aligned exactly with any of the faces of the package; consequently, the data must then be analyzed to determine the orientation of the vector relative to the established reference plane. (Further evaluation is required to determine the polarity of the vector.) Referring to Fig. 3, the parameters of the vector relative to the established axes can be calculated as:
|Γ| = (Γx2 + Γy2 + Γz2)0.5 (4)
|Γ|= (Γx2 + Γy2)0.5 (5)
Φ = cos-1(Γx/Γxy (6)
θ = sin-1(Γz/|Γ|) (7)
Equation 4 gives the maximum sensitivity that will be exhibited when the force applied is exactly parallel to the direction of the vector. When specifying a crystal, this is sometimes referred to as Γmax or the total vector. This value will always be greater than the magnitude measured along one of the orthogonal axes of the oscillator unless the vector is exactly aligned with an axis. Once the magnitude and the angular orientation of Γ have been determined, it is then possible to predict the oscillator performance under other vibratory conditions.
If the oscillator in use will experience vibration at a single frequency, then the previous formulas will show the level of the sidebands that will be produced if the applied g level is known. However, in most real-world applications, the vibration energy will be spread across a frequency band, producing a random vibration profile. The shape of this profile will be highly application specific with most of the energy typically ranging from as low as 5 or 10 Hz through as high as 10 to 20 kHz. There may be peaks in the response where the energy is concentrated depending upon the source of the vibration and the mechanical mounting of the components.
This noise-like random energy is expressed as a power spectral density with units of g2/Hz. Rather than producing a discrete spurious signal product in the spectrum as with sine vibration, random vibration will cause the phase-noise floor of the oscillator to rise across the frequency band of vibration. The same basic calculation is then performed to predict the effect on the oscillator spectrum but the vibration energy is now expressed as g2/Hz, giving the following formula for the single-sideband phase noise of the oscillator under vibration:
L(fv) = 20log[|Γ| · fnom(2PSD)0.5/2fv] (8)
where PSD = the power spectral density of the vibration at frequency fv.
Under random vibration, the entire noise floor of the oscillator will increase across the range of vibration frequencies. The acceleration sensitivity could then be determined by measuring the phase noise of the oscillator while vibrating.
This file type includes high resolution graphics and schematics when applicable.
Meeting Expectations
This file type includes high resolution graphics and schematics when applicable.
To ensure that an oscillator will meet the performance requirements in the final application environment, it is necessary to make sure that the manufacturer understands the details of the application. These include the expected vibration levels and frequencies and the required performance required under these conditions.
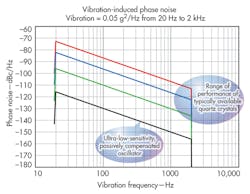
Crystal oscillators are available in a multitude of different configurations, running the gamut from simple clock oscillators costing less than $1 to precision ovenized oscillators for specialized applications that may cost thousands of dollars. While the overall frequency stability of the different types of oscillators may vary by more than 10,000 to 1, the acceleration sensitivity of any type of crystal oscillator will rarely vary from 1 ppb/g by more than a factor of 4 (ranging from around 0.25 ppb/g for some selection of specialized crystals to as high as 4 ppb/g for some typical standard low-cost crystals.)
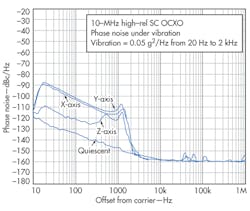
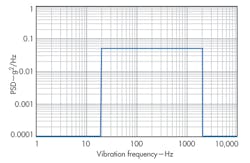
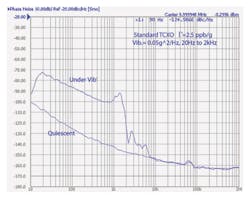
As Fig. 5 shows, the vibration-induced phase noise of any type of typical crystal would fall within about 30 dB of any other type under the same conditions. It should not be assumed that just by specifying a more precision oscillator with better frequency stability and static phase noise that the performance under vibration will likewise be improved. In many cases, a more precision oscillator will use a crystal that still has similar acceleration characteristics to a less-expensive one. Figure 4 shows the degradation in phase noise that occurs on a high-reliability 10-MHz OCXO with a precision “SC” cut crystal under a flat random vibration profile of 0.05 g2/Hz from 20 Hz to 2 kHz (Fig. 6). Γmax for this oscillator is measured at 7 × 10-10/g, which is typical for a standard 10 MHz third-overtone SC-cut crystal in a round HC-37 holder with a four-point mount.
This overall vibration profile is commonly used for oscillator evaluation since the effects due to the oscillator itself over the vibration frequency range are more apparent. Even though the oscillator shown in Fig. 4 is a very stable device with overall stability of better than 0.01 ppm, it can be seen that even this relatively modest vibration causes significant degradation in the short-term stability and phase noise.
This file type includes high resolution graphics and schematics when applicable.
Acceleration Sensitivity
This file type includes high resolution graphics and schematics when applicable.
Although the frequency stability of a typical TCXO is more than an order of magnitude worse than a precision OCXO, their acceleration sensitivities are often similar. This means that their dynamic stability and phase noise will also be similar since the vibratory performance is determined by the Γ characteristic and the applied acceleration level and is largely independent of the static phase noise and frequency stability. Unless Γ and/or a are extremely small, any random vibration will cause the noise floor of the oscillator to rise. The phase noise degradation that occurs in a 10-MHz TCXO with Γ of 2.5 ppb/g is shown in Fig. 7.
If it is determined that the acceleration sensitivity of an oscillator must be improved to meet system specifications, there are several approaches that can be considered. If the highest vibration levels come primarily along one axis, it may be possible to mount the oscillator so that the Γ vector is perpendicular to the axis of vibration o that the vibration is applied along the plane of “zero” sensitivity. In some instances, a 10:1 improvement could be realized with this approach. In most real-world applications, however, there is significant vibration present in all axes, so this approach may be of limited benefit.
Special crystal design techniques can be used to reduce the acceleration sensitivity to some degree. Precision SC-cut resonators that employ unique stress relieved mounting structures are available that exhibit acceleration sensitivities as low as 0.2 ppb/g. Other crystals, such as certain rectangular strip-type crystals, can be manufactured with special mountings that achieve sensitivities as low as 0.1 ppb/g with some yield.
Mechanical vibration isolators can be effective in some applications by reducing the vibration energy that is conducted to the oscillator. Isolators act as lowpass filters: attenuating the vibration energy above their natural resonant frequency, but passing all of the energy below said frequency. This frequency is dependent upon the stiffness of the isolator and the weight of the supported assembly. With a small, lightweight assembly such as an oscillator, it is difficult to achieve effective attenuation below a few hundred Hz. And depending upon the “Q” of the structure, the vibration energy is actually amplified near the natural frequency. Care must be taken to ensure sufficient “sway room” to allow for movement of the assembly, especially if excited near the resonant frequency.
Other considerations with mechanical isolators include directional dependence, changes in their stiffness over temperature, additional weight to lower the resonant frequency, and the space required to mount the assembly. A properly designed isolation system can be quite effective in reducing high-frequency vibration energy. However, a system which is not properly designed can actually make performance worse under some conditions.
Even after many years of work, there has been little progress in producing resonators with sensitivities below the low parts in 1010/g level. In order to achieve better performance, some sort of compensation must be used. There are two basic types of compensation: active and passive. Active techniques employ an acceleration-sensitive component such as an accelerometer to sense the applied vibration or acceleration. That signal is then processed with the proper amplification and phase reversal and fed back to the oscillator to cancel the effects of the vibration on the resonator.
This method can be quite effective, producing oscillators with Γ to low parts in 1012/g at lower vibration frequencies. But as the vibration frequencies increase beyond about several hundred Hz, it becomes very difficult to maintain the amplitude and phase linearity required to sustain those levels for cancellation. And adding the required circuitry significantly increases the size and cost of the oscillator.
Passive compensation methods employ multiple crystals which are carefully aligned to that their Γ vectors are aligned anti-parallel (pointing in exactly opposite directions). The acceleration-induced positive frequency shift of one resonator is therefore cancelled by a corresponding negative shift from the other resonator. The crystals are connected either in series or in parallel in the oscillator circuit and function as a single composite resonator.
This method has been known for more than 30 years,6 but has historically been difficult to implement due to lack of consistency in the Γ vectors of conventional crystals. Both the magnitude and the direction of Γ must be matched closely if significant cancellation is to occur. Recent advances in small AT-cut strip crystals designed for rugged applications have achieved better consistency in the Γ vector, enabling practical designs that achieve sensitivities in the low parts in 1011/g.7
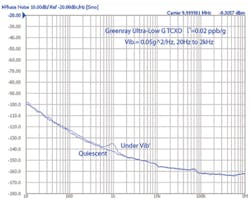
Passively compensated TCXOs are now available that provide ultralow acceleration sensitivity in all axes. The performance of a passively compensated TCXO is shown in Fig. 8. Even under the same moderate random vibration, as shown in Fig. 6, the vibration induced noise is still below the quiescent phase noise of the oscillator since |Γ| is a very low 0.02 ppb/g or 2 × 10-11/g. Oscillators of this type are being produced to frequencies greater than 100 MHz.8 For applications where operation in the presence of significant vibration is required, this type of passively compensated crystal oscillator may provide the best combination of critical performance for the cost.
This file type includes high resolution graphics and schematics when applicable.
References
This file type includes high resolution graphics and schematics when applicable.
1. R.L. Filler, “The Acceleration Sensitivity of Quartz Crystal Oscillators: A Review,” Proceedings of the 42nd Annual Symposium on Frequency Control, 1988, pp. 297-305.
2. J.M. Przyjemski, “Improvement in system performance using a crystal oscillator compensated for acceleration sensitivity,” Proceedings of the 32nd Annual Symposium on Frequency Control, 1978, pp. 426-431.
Related Articles
• Connector Couples High-Speed Signals
• Oscillators Are Steady With Temperature
• Microwave Diodes… Why a Schottky-barrier? Why a Point-contact?
3. R.L. Filler, “The effects of vibration on frequency standards and clocks,” Proceedings of the 35th Annual Symposium on Frequency Control, 1981, pp. 31-39.
4. J.R. Vig, “Quartz crystal resonators and oscillators for frequency control and timing applications—A Tutorial,” Rev. 8.5.3.0, February 2005, AD-M001251 (revised).
5. A. Warner et al., “Low ‘g’ sensitivity crystal units and their testing,” Proceedings of the 33rd Annual Symposium on Frequency Control, 1979, pp. 306-310.
6. Filler, “Acceleration resistant crystal resonator, United States Patent No. 4,410,822, 1983.
7. S. J. Fry and G. Burnett, “Reducing the acceleration sensitivity of AT-strip quartz crystal oscillators,” Proceedings of the 2010 IEEE Frequency Control Symposium, 2010.
8. S. J. Fry, et al., “Crystal oscillator with reduced acceleration sensitivity,” United States Patent No. 8,188,800, 2012.
This file type includes high resolution graphics and schematics when applicable.