Fast Numerical Analysis of Scattering and Radar Cross Section (.PDF Download)

The ability to avoid enemy radar requires that modern fighter aircrafts, ships, and missiles have a very small radar cross section (RCS). Researchers and engineers are working on making these stealth objects rely on computational electromagnetics (EM) to optimize the RCS and scattering effects of an arbitrary object using radars. An object exposed to EM waves scatters the incident energy in all directions. The energy that returns to the source of the EM wave, known as backscattering, is the “echo” of the object. The intensity of the radar echo is what we refer to as RCS.

Best practices use a sphere to calibrate radar systems because a sphere will return an echo signal back to the target that sent it. The RCS wavelength consists of three parts: the Rayleigh, Mie, and optical region. The Mie and optical regions are of particular interest, because the analytical solution of the RCS is well-known.

Back to RCS Basics

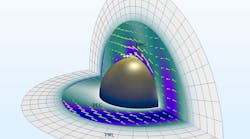
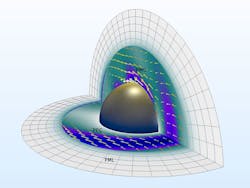
A classic benchmark example of Mie scattering of a sphere is a great place to start when examining this problem. In the following example, a plane wave illuminates a metallic sphere in free space, and its RCS is computed. The geometry consists of two concentric spherical shells (Fig. 1). The innermost shell, adjacent to the sphere, represents the free-space domain, and the second shell represents a perfectly matched layer (PML) region.